一种工业机器人动力学参数复合辨识方法

本发明涉及工业机器人，特别涉及一种工业机器人动力学参数的辨识方法。

背景技术：

1、工业机器人在多个行业得到了广泛应用，极大提高了生产力，随着科技的发展，人们对工业机器人的性能要求更高，要求其实现功能更复杂，传统的pid控制已经无法满足对工业机器人进行高精度控制的需求。因此，基于工业机器人机理模型来实现高精度控制的方法将成为主流。基于模型的工业机器人控制器以机器人动力学模型作为先验值，但是工业机器人是一种多变量、强耦合的非线性系统，通过数学计算获得动力学模型很困难。

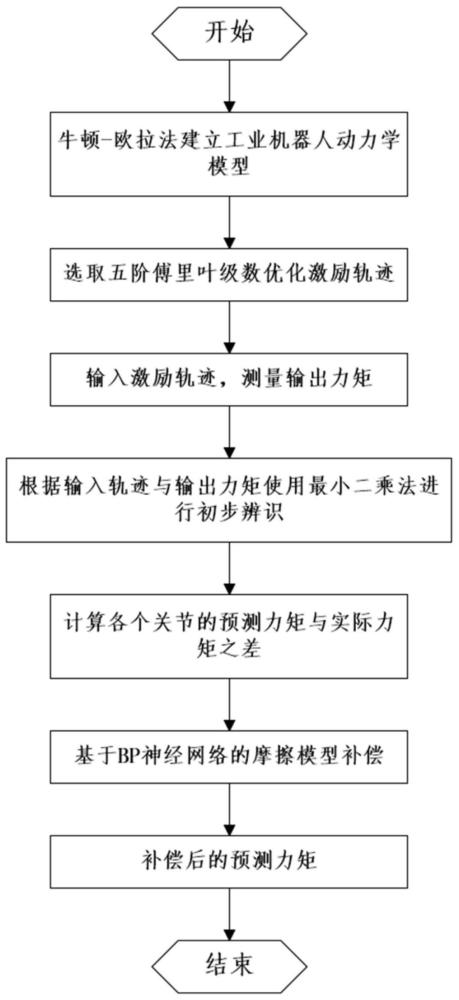
2、目前，常用辨识方法先通过牛顿-欧拉法进行动力学建模，创建机器人的动力学模型，然后通过参数重组得到可辨识的最小参数集，并设计最优激励轨迹得到一组有效输入输出数据用于机械臂的动力参数辨识，通过合理的参数辨识方法对工业机器人进行参数辨识，获得工业机器人的准确机理模型，最后通过bp神经网络对摩擦力矩进行有效补偿，提高输出力矩的预测精度，从而为后续对工业机器人高精度控制研究的开展提供有力保障。

3、目前，国内外已有大量关于工业机器人动力学参数辨识的研究，提出了多种有效的工业机器人参数辨识方法。

4、祖丽楠等人在申请号为202111654616.7,名称为“一种基于遗传算法优化的神经网络机械臂动力学建模方法”的专利申请中提出了一种基于神经网络的机械臂网络模型建模方法，该方法通过一种基于遗传算法优化的神经网络建立了机械臂网络模型，所建网络模型机准确反映了机械臂的关节运动变量与输出力矩间的关系。但该方法不考虑辨识对象内部结构，而是将整个系统看作一个“黑箱”，无法得到所辨识系统内部具体动力学参数，因此依靠该方法无法得到工业机器人准确的机理模型来实现对工业机器人的高精度控制。

5、在题为“工业机器人动力学参数辨识及软件系统开发”的文章中，作者屈艺丹通过牛顿-欧拉法对工业机器人进行动力学建模，选择有穷傅里叶级数做为最优激励轨迹的表达式，通过最小化退化矩阵的条件数来获得最优激励轨迹中的参数，同时把各关节位置、速度和加速度的物理约束与激励轨迹结合起来，使获得的最优激励轨迹在物理意义上是可行的，通过在激励轨迹中指定频率范围来避免激励机器人的柔性特性，最后利用最小二乘法实现了机械臂动力学参数辨识。该方法能够在观测数据集正确的情况下，实现工业机器人的最小动力学参数集辨识，但由于最小二乘法自身的特点，以及机器人摩擦力模型的复杂与非线性，摩擦力的输出力矩存在不可避免的动态误差，当观测数据集中存在异常数据时，辨识参数精度会大大降低，导致所建立动力学模型不准确。

6、在题为“基于免疫算法和神经网络的机械臂动力学参数辨识与验证”的文章中，作者泮求亮针对传统激励轨迹设计以傅里叶级数形式展开，会导致机械臂启停过程中产生抖动，导致跟随轨迹精度降低的问题，通过免疫克隆算法优化，得到一条首尾封闭，抗噪声能力强的较优激励轨迹，并通过神经网络来辨识动力学参数，相较于传统最小二乘辨识方法，该方法有效提高了工业机器人动力学参数辨识的准确性和可靠性。但该方法在进行工业机器人参数辨识时采用的神经网络过于简单，仅设置一层隐藏层，导致所用网络性能较差，可能出现训练过程收敛慢甚至不收敛的问题。

技术实现思路

1、有鉴于此，本发明的目的是提供一种工业机器人动力学参数复合辨识方法，以解决工业机器人关键动力学参数辨识问题，帮助准确建立工业机器人机理模型，为后续开展工业机器人高精度控制打下良好基础。

2、本发明工业机器人动力学参数复合辨识方法包括：

3、步骤一：通过牛顿-欧拉法建立工业机器人动力学模型，再将工业机器人动力学模型线性化，得到工业机器人动力学方程的线性分离形式：

4、

5、其中：τ表示工业机器人各个关节的输出力矩，为工业机器人各个关节当前角度q、角速度角加速度组成的系数矩阵，p为可辨识的参数集；

6、

7、其中：下标j表示工业机器人的自由度，p是由p1到pj组成的列向量；为工业机器人的连杆i的惯性张量集合，mj、rjx、rjy、rjz为连杆i的质量与质心分量，iaj为关节i的电机等效转动惯量，fcj、fvj为库伦摩擦力系数和粘滞摩擦力系数；

8、步骤二：采用五阶傅里叶级数作为工业机器人的激励轨迹：

9、

10、其中：q0表示激励轨迹的补偿量，为常数；n＝5表示傅里叶级数的阶次；ai,bi分别表示傅里叶级数中正弦项、余弦项的幅值；ωf表示傅里叶级数的频率；k为周期采样数，ts为采样周期；

11、步骤三：控制工业机器人按步骤二设计的激励轨迹运动，并对工业机器人在不同时刻的关节力矩和关节角度信息进行采样，得到：

12、γn＝wn·p                         (4)

13、其中表示观测力矩，观测矩阵中为第n个采样点的系数矩阵；

14、对上述n阶非齐次方程组γn＝wn·p，考虑观测矩阵和输出力矩的扰动δwn和δγn，得到添加扰动后的方程：

15、(γn+δγn)＝(wn+δwn)·(p+δp)                     (5)

16、其中δp为最终辨识结果中的误差；

17、步骤四：基于步骤一建立的工业机器人动力学方程与步骤三产生的观测数据，使用最小二乘法辨识得到工业机器人的动力学参数：

18、p＝(yty)-1ytt                         (6)；

19、其中：观测矩阵观测响应下标m表示数据点的个数；

20、步骤五：通过bp神经网络对摩擦力矩进行补偿，包括：

21、对步骤四辨识后得到的结果，计算实际力矩与由最小二乘法辨识得到的结果预测的输出力矩之差，以此来估计摩擦力的大小：

22、

23、其中：w为各关节输入激励轨迹得到的观测矩阵，为最小参数集合中不包含摩擦力参数的常规参数集合，实际力矩的表达式如下γ：

24、

25、其中：为最小参数集合中的摩擦力参数集合，ε为误差变量；

26、以作为bp神经网络的输入，以作为bp神经网络训练数据的期望输出，对bp神经网络进行训练；其中为连杆i的第k个采样点的加速度，为连杆i的第k个采样点使用初步辨识得到的摩擦力参数，通过库伦-粘滞摩擦力模型求得的预测输出摩擦力，sign()表示符号函数；

27、训练结束后，将给定验证轨迹的速度符号函数使用辨识结果求得的摩擦力作为训练好的bp神经网络的输入，得到验证输出γf；使用该验证输出代替摩擦力矩与预测力矩相加来得到最终的预测力矩

28、

29、进一步，在步骤三控制工业机器人按步骤二设计的激励轨迹运动中，对工业机器人设置如下约束条件：

30、条件一：

31、

32、条件二：

33、

34、条件三：

35、τi,min≤τi≤τi,max                        (11)

36、条件四：

37、

38、其中：qi,max，qi,min分别表示工业机器人连杆i的关节角度上限与角度下限；表示连杆i的关节角速度上限；表示连杆i的关节角加速度上限；qi,init表示连杆i的初始关节角度；t为傅里叶级数周期；τi,max，τi,min为连杆i允许的驱动力矩最大最小值；{s(q(t))}表示工业机器人t时刻的末端运动位置；s表示工业机器人的运动空间。

39、本发明的有益效果：

40、1、本发明将激励轨迹设计为五阶傅里叶级数，该方法能为工业机器人提供合适的激励轨迹参数。利用傅里叶级数周期性性质，通过多周期采样再平均的方法，有效降低了噪声等干扰因素对观测数据集的影响，极大提高了观测数据集精度。

41、2、相较于传统最小二乘回归参数辨识法受异常数据干扰大，稳定性差；一般线性摩擦力模型辨识对摩擦力矩表述的不准确问题和非线性摩擦力模型辨识时带来的不确定性误差等问题，本发明通过训练bp神经网络得到的摩擦模型对摩擦参数进行补充，该方法有效减小了预测摩擦力矩的偏差，提高了工业机器人动力学参数辨识准确性，为后续开展工业机器人高精度控制研究打下了良好基础。

42、3、本发明针对传统激励轨迹设计中未考虑工业机器人激励过程中发生抖动，而缺少必要约束条件，导致激励过程中抖动严重的现象。在约束条件中增加了初始与周期末机器人关节速度与加速度限制，有效减少了激励过程中机器人的抖动。