层状节理岩体三维等效连续本构模型构建方法

本发明涉及岩土工程本构模型研究，具体涉及一种层状节理岩体三维等效连续本构模型构建方法。

背景技术：

1、自然界中具有层状构造的沉积岩约占陆地总面积的60％以上，部分变质岩也具有显著的层状构造特征，因此许多大型水利水电工程不可避免地会建设在具有层状岩体的复杂地质环境中。

2、由于在形成过程中经历了复杂的地质构造作用，层状岩体表现出较为特殊的赋存特征，不仅具有定向成层的主级层面(层理、片理等)，而且往往分布有贯穿或非贯穿的次级结构面(切层节理组、层内随机裂隙等)，形成一种包含主、次级结构面的“二级结构”，使其表现出更为复杂的各向异性特征。

3、层状节理岩体的力学各向异性是其区别于其他岩体最重要的特性，也是岩石力学领域的研究热点和难点。数值分析方法是研究层状节理岩体力学各向异性的有力手段，在进行层状节理岩体分析计算时，层面通常有显式和隐式两种实现方式。显式方法主要通过节理单元或接触面单元来模拟层面，能够实现层状节理岩体结构的物理还原，模型的各项参数物理意义清晰、概念明确，但模型建立过程较复杂，且计算效率较低，对于当前的计算能力，庞大的模型和计算体量也成为了工程尺度(百米、千米级)精细分析的壁垒；隐式方法是将层状节理岩体等效为连续介质，通过在本构模型中考虑层面的作用来数学等效层状节理岩体的力学行为，由于在模型建立和单元划分中无需考虑层面，该方法也是目前大规模层状工程岩体分析采用的主要方法。但隐式方法合理与否的关键在于其本构模型是否能够准确反映层状节理岩体的变形和强度各向异性，变形各向异性主要通过应力应变关系表征，强度各向异性通过强度准则来描述。

4、由于层状岩体各向异性的复杂性，目前除遍布节理本构模型外，其他能够描述层状节理岩体各向异性的本构模型大多还处于理论研究阶段，在实际工程中应用较少，究其原因在于：①各向异性应力应变关系和强度准则十分复杂，参数多，且取值困难；②各向异性力学模型往往无法用显式的数学公式表达，计算过程复杂，计算量巨大，计算效率低。

技术实现思路

1、本发明提出了一种层状节理岩体三维等效连续本构模型构建方法，以解决本构模型中力学参数不明确，取值困难，计算量庞大的技术问题。

2、为解决上述技术问题，本发明提供了一种层状节理岩体三维等效连续本构模型构建方法，包括以下步骤：

3、步骤s1：建立本构模型的应力应变关系：

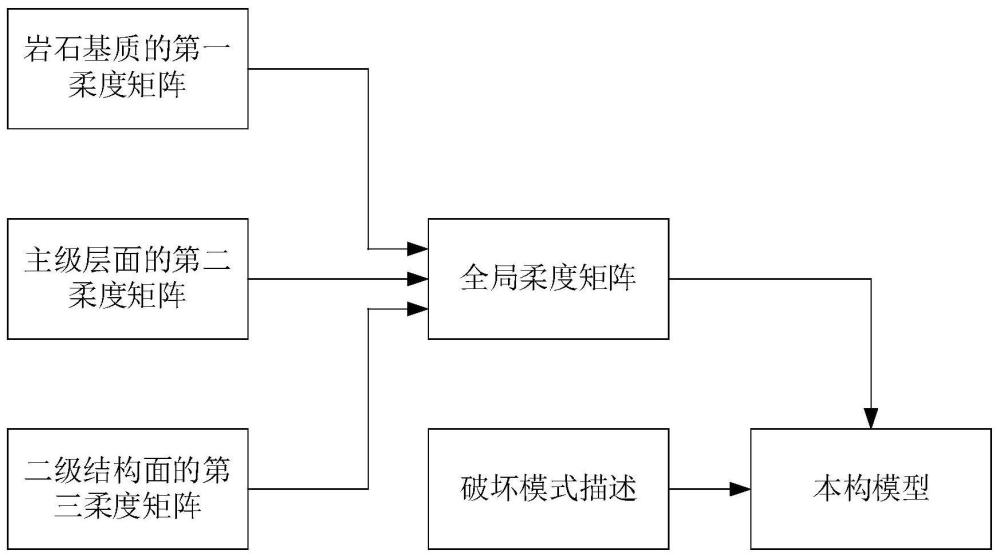
4、构建岩石基质的第一柔度矩阵；构建主级层面的第二柔度矩阵；构建二级结构面的第三柔度矩阵；

5、将所述第一柔度矩阵、第二柔度矩阵和第三柔度矩阵进行相加，得到全局柔度矩阵；

6、步骤s2：对所述岩石基质、主级层面和二级结构面进行破坏模式描述，以构建所述本构模型的强度准则。

7、优选地，所述第一柔度矩阵的构建方法包括：

8、将岩石基质视为各向同性弹性体，根据广义胡克定律，得到所述岩石基质柔度矩阵的表达式为：

9、

10、式中，e和v分别代表岩石基质的杨氏模量和泊松比，δ表示克罗内克函数，i＝1,2,3；j＝1,2,3；k＝1,2,3；l＝1,2,3；

11、转化为矩阵形式，表示为：

12、

13、式中，g表示岩石基质的剪切模量。

14、优选地，所述第二柔度矩阵的构建方法包括：

15、采用局部坐标系描述主级层面的本构关系：

16、

17、式中，i＝1,2,3；j＝1,2,3；k＝1,2,3；l＝1,2,3，为体积为v的表征单元体内主级层面引起的平均应变，表示局部层理面柔度矩阵，σ表示应力张量；

18、在局部坐标系下将所述局部层理面柔度矩阵进行展开：

19、

20、式中，s分别为主级层面的法向刚度矩阵、切向刚度矩阵和主级层面之间的平均间距；

21、将所述局部层理面柔度矩阵转化为层理面柔度矩阵：

22、

23、

24、l1＝sin(dip)*cos(dd),l2＝-cos(dd),l3＝sin(dd)*sin(dip)

25、m1＝cos(dd)cos(dip),m2＝sin(dd),m3＝cos(dd)

26、n1＝-sin(dip),n2＝0,n3＝cos(dip)

27、式中，q为局部到全局的转换矩阵；qt为转换矩阵的转置矩阵；dip为主级层面倾角；dd为主级层面倾向；li,mi,ni表示主级层面的法向余弦。

28、优选地，所述第三柔度矩阵的表达式为：

29、对于连续形式，表示为：

30、

31、对于离散形式，表示为：

32、

33、

34、式中，i＝1,2,3；j＝1,2,3；k＝1,2,3；l＝1,2,3，表示体积为v的表征单元体内二级结构面的平均应变；表示二级结构面的柔度矩阵；为表征单元体内的平均应力；ρ表示裂隙密度；rmax表示裂隙最大有效直径；ω表示固体角，a()表示裂隙等效直径为r的面积；r表示裂隙等效直径；e(n,r)表示裂隙方位分布的概率密度函数；表示平均位移跳跃；δ表示克罗内克函数；n表示裂隙法向向量；f表示裂隙二阶张量；平均应力张量；n表示裂隙数量；v表示泊松比；e表示岩石基质的弹性模量。

35、优选地，所述全局柔度矩阵的表达式为：

36、

37、式中，i＝1,2,3；j＝1,2,3；k＝1,2,3；l＝1,2,3，表示岩石基质柔度矩阵；表示层理面柔度矩阵；表示切层节理组和随机离散裂隙的柔度矩阵；υ表示泊松比；e表示岩石基质的弹性模量；δ表示克罗内克函数；qi表示局部坐标系和全局坐标系之间的转换矩阵；表示局部坐标系下次级结构面的柔度张量。

38、优选地，对所述岩石基质进行破坏模式描述的方法包括：设定压应力为负，拉应力为正，屈服准则选用带拉伸截止的限的mohr-coulomb屈服准则：

39、

40、ft＝σ3-σt(tension)；

41、

42、fs＝0；

43、ft＝0；

44、

45、

46、

47、式中，fs表示剪切屈服准则，ft表示拉伸屈服准则，h表示剪切拉伸屈服准则边界函数，c，和σt分别是岩石基质的黏聚力、内摩擦角和抗拉强度，表示岩石基质的剪胀角函数，σ1和σ3分别表示最大主应力和最小主应力；

48、抗拉强度σt的最大值σmaxt满足以下公式：

49、

50、采用如下流动法则：

51、

52、

53、式中，ψ为岩石基质的剪胀角，gs和gt分别表示岩石基质的剪切流动法则和拉伸流动法则。

54、优选地，对所述主级层面进行破坏模式描述的方法包括：设置局部坐标系，所述局部坐标系的3轴垂直于主级层面，1轴指向主级层面的倾角方向，2轴指向主级层面的走向方向；

55、屈服准则采用带拉伸截止的mohr-coulomb屈服准则：

56、

57、fj0t＝σ3'3'-σj0t(tension)；

58、hj0＝τj0-aφj0+bφj0(σ3'3'-σj0t)(shear tension boundary)

59、fj0s＝0；

60、fj0t＝0；

61、

62、式中，fj0s表示剪切屈服准则，fj0t表示拉伸屈服准则，hj0表示剪切拉伸屈服准则的边界函数，σ1'3'，σ2'3'和σ3'3'分别是主级层面的局部坐标系下的应力张量分量，cj0，和σj0t分别是主级层面的黏聚力、内摩擦角和抗拉强度，τj0表示表示主级层面上的剪切应力总量值；

63、当主级层面的内摩擦角非0时，抗拉强度的最大值满足：

64、

65、优选地，所述二级结构面通过损伤力学理论进行破坏模式描述。

66、优选地，所述二级结构面进行破坏模式描述的方法包括：设定岩体内的节理和裂隙面为平面且损伤沿着微裂隙的界面扩展，以微裂隙单元为基准设定三轴垂直的坐标系x、y和z；

67、垂直于x、y、z轴方向的所有微立方体的总有效表面积a，表达式为：

68、

69、式中，v和v分别是微裂隙单元和表征单元体的体积，v的边长为hv；

70、仅考虑垂直于z轴方向的微裂隙，则微立方体沿z方向有效表面积az表示为：

71、

72、设定在v内有n条裂隙，第k条裂隙的表面积为ak，单位法向矢量为nk，将岩体的损伤变量ωk定义为损伤面积与总面积比值，则损伤变量ωk的表达式为：

73、

74、二阶损伤张量ωk表示为：

75、

76、对体积v内的全部切层节理组和随机离散裂隙等次级结构面的损伤求和得到表征单元体内的总损伤张量ω为：

77、

78、根据下式求得次级结构面对主级层面的损伤变量ωj0：

79、ωj0＝n·ω·n；

80、式中n表示裂隙单位法向向量；

81、二阶损伤张量的三个不变量i1ω,i2ω,i3ω表示为：

82、i1ω＝ω1+ω2+ω3

83、i2ω＝-(ω1ω2+ω1ω3+ω2ω3)；

84、i3ω＝ω1ω2ω3

85、式中，i1ω、i2ω、i3ω分别表示二阶损伤张量的第一不变量、第二不变量和第三不变量；ω1、ω2、ω3分别表示表征单元体内的总损伤张量ω的三个主值。

86、本发明的有益效果至少包括：本发明基于裂隙张量理论，在复合层状岩体本构模型基础上建立综合考虑岩石基质、主级层面、切层节理组或随机裂隙的影响的三维等效层状节理岩体力学模型(layerdfn)，本构模型中力学参数明确，便于取值，计算结果合理。