一类符合全驱形式系统的控制律设计方法

本发明属于系统与控制领域，具体来说，涉及了一类符合全驱形式系统控制律设计的方法。

背景技术：

1、所有实际系统都有物理背景，当用拉格朗日方程或动量定理等物理定律对系统进行建模时，往往会得到一个二阶或更高阶的模型，而这个原始模型在某些方面也反映了系统的物理背景。在某些情况下，背景信息可能有助于分析和设计。然而，在一阶系统方法中，系统模型被简化成了一阶状态空间模型，这就导致了在原始模型中去除了系统的背景信息。

2、由于非线性系统是广泛存在的，复杂的非线性会使得使李雅普诺夫函数的分析变得更加困难，因此传统的状态空间法在处理系统控制方面存在一定的局限性；尽管状态空间法在处理响应分析和观测等问题时有一定的优势，但这种方法没有把系统的控制变量作为重点；由于全驱特性允许对消掉开环系统的所有动态特性(无论是线性还是非线性的)，同时建立全新的希望的闭环动态特性，将一类符合全驱形式系统转化为全驱系统来进行处理时，可以利用这一特性来将一些复杂的问题简单化，从而使系统分析和设计的理论更具有实用性。

3、从物理学的角度来看，世界上有许多完全驱动系统，它们的原始系统模型都是由一定的物理定律建立的二阶或高阶模型。完全驱动的物理概念可以在数学上概括为描述各种控制系统，线性化系统、反馈线性化系统以及一些其他更一般类型的非线性系统都可以等价地转换为全驱系统形式。在系统建模过程中，利用一定的物理量得到一系列二阶系统形式的子系统，一方面，可以通过变量扩张，或等价地通过定义一个状态向量，进一步得到一阶状态空间形式的系统；另一方面，可以通过变量消去的方法最终得到全驱系统。对于这样一个系统，可以通过设计一个全驱控制器来消除系统中存在的非线性，从而得到一个恒定的线性闭环系统，使后续的系统分析变得更加的简洁。

技术实现思路

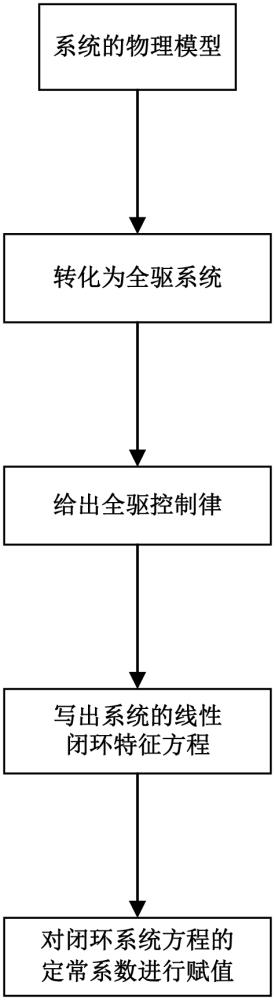
1、本发明的目的是通过将一类符合全驱形式的系统转化为全驱系统，消除开环系统的所有动态特性，并给出一个希望的任意可配置特征结构的定常线性闭环系统。本发明通过对一类符合全驱形式的具体系统的研究，给出了由系统的物理模型向全驱形式的转化步骤，以及全驱控制器的设计方法，并利用全驱特性允许对消掉开环系统的所有动态特性的特点，获得了一个希望的定常线性闭环系统。

2、本发明第一方面提供一种一类符合全驱形式系统的控制律设计方法，该方法包括以下步骤：

3、(1)完成由系统物理模型到全驱系统的转化，获得系统的全驱系统形式，包括以下步骤：

4、步骤101、基于已知的物理定律获得系统所对应的物理模型；

5、

6、其中，x和u分别是系统的状态向量与输入向量；θ是系统的虚拟控制量，且

7、步骤102、将步骤101中系统的物理模型转化为全驱系统模型；

8、将公式(1)中的第一个方程进行转化，得到如下公式：

9、

10、其中x是系统的状态向量；θ是系统的虚拟控制量；

11、步骤103、将步骤102中所得到的公式(2)再求导后进行整理，得如下公式：

12、

13、其中x是系统的状态向量；θ是系统的虚拟控制量；

14、步骤104、将步骤103中得到的公式(3)代入到步骤101中的公式(1)的第二个方程并进行整理，即得到系统的全驱形式：

15、

16、其中x和u分别是系统的状态向量与控制输入向量；

17、步骤105、令和将其代入到步骤104中；则公式(4)改写成如下形式：

18、x(4)＝f(·)+l(·)u                                                (5)

19、其中l(·)是连续的矩阵函数，且detl(·)≠0；f(·)是连续的向量函数；

20、(2)完成对系统全驱控制律的设计，获得所需的定常线性闭环特征方程，并对闭环系统方程的定常系数进行赋值，包括以下步骤：

21、步骤201、对于任意给定的线性定常矩阵，给出系统在全驱形式下的控制律：

22、

23、其中，x(i),i＝0,1,2,3是系统的状态向量；v是设定值；l(·)是连续的矩阵函数；f(·)是连续的向量函数；

24、步骤202、由步骤201中所写出的全驱控制律，获得系统希望的线性定常闭环特征方程如下：

25、

26、其中，x(i),i＝0,1,2,3,4是状态向量；v是设定值；ai,i＝0,1,2,3是期望闭环系统方程的定常系数；

27、步骤203、对步骤202中所获得的线性定常闭环特征方程，通过引入微分环节的四阶展开式来对方程系数ai,i＝0,1,2,3进行赋值；

28、

29、其中t是微分时间常数；s是微分算子；

30、步骤204、将步骤202中的线性定常闭环特征方程与步骤203中所得到微分四阶展开式相对应，得到ai,i＝0,1,2,3的值；

31、

32、步骤205、对t进行赋值，完成全驱系统的控制律的设计，得到系统希望的线性定常闭环特征方程。

33、本发明第二方面提供一种一类符合全驱形式系统的控制律设计系统，包括：

34、全驱系统形式转化模块，用于完成由系统物理模型到全驱系统的转化，获得系统的全驱系统形式；

35、所述全驱系统形式转化模块通过以下步骤实现其功能：

36、步骤101、基于已知的物理定律获得系统所对应的物理模型；

37、

38、其中，x和u分别是系统的状态向量与输入向量；θ是系统的虚拟控制量，且

39、步骤102、将步骤101中系统的物理模型转化为全驱系统模型；

40、将公式(1)中的第一个方程进行转化，得到如下公式：

41、

42、其中x是系统的状态向量；θ是系统的虚拟控制量；

43、步骤103、将步骤102中所得到的公式(2)再求导后进行整理，得如下公式：

44、

45、其中x是系统的状态向量；θ是系统的虚拟控制量；

46、步骤104、将步骤103中得到的公式(3)代入到步骤101中的公式(1)的第二个方程并进行整理，即得到系统的全驱形式：

47、

48、其中x和u分别是系统的状态向量与控制输入向量；

49、步骤105、令和将其代入到步骤104中；则公式(4)改写成如下形式：

50、x(4)＝f(·)+l(·)u                                               (5)

51、其中l(·)是连续的矩阵函数，且detl(·)≠0；f(·)是连续的向量函数；

52、全驱控制律设计模块，用于完成对系统全驱控制律的设计，获得所需的定常线性闭环特征方程，并对闭环系统方程的定常系数进行赋值；

53、所述全驱控制律设计模块通过以下步骤实现其功能：

54、步骤201、对于任意给定的线性定常矩阵，给出系统在全驱形式下的控制律：

55、

56、其中，x(i),i＝0,1,2,3是系统的状态向量；v是设定值；l(·)是连续的矩阵函数；f(·)是连续的向量函数；

57、步骤202、由步骤201中所写出的全驱控制律，获得系统希望的线性定常闭环特征方程如下：

58、

59、其中，x(i),i＝0,1,2,3,4是状态向量；v是设定值；ai,i＝0,1,2,3是期望闭环系统方程的定常系数；

60、步骤203、对步骤202中所获得的线性定常闭环特征方程，通过引入微分环节的四阶展开式来对方程系数ai,i＝0,1,2,3进行赋值；

61、

62、其中t是微分时间常数；s是微分算子；

63、步骤204、将步骤202中的线性定常闭环特征方程与步骤203中所得到微分四阶展开式相对应，得到ai,i＝0,1,2,3的值；

64、

65、步骤205、对t进行赋值，完成全驱系统的控制律的设计，得到系统希望的线性定常闭环特征方程。

66、本发明第三方面提供一种设备，包括：

67、一个或多个处理器；

68、存储器，用于存储一个或多个程序，

69、当所述一个或多个程序被所述一个或多个处理器执行时，使得所述一个或多个处理器执行如所述的一类符合全驱形式系统的控制律设计方法。

70、本发明第四方面提供一种存储有计算机程序的计算机可读存储介质，该程序被处理器执行时实现如所述的一种一类符合全驱形式系统的控制律设计方法。

71、本发明相对于现有技术具有突出的实质性特点和显著进步，具体来说：

72、本发明能够将一类符合全驱形式的系统转化为全驱系统，并且利用全驱特性消掉开环系统的所有动态特性，即使在非线性系统的情况下，也能获得一个希望的定常线性闭环系统，解决了许多李亚普诺夫方法不能解决的非线性控制问题。