一种速度规划最优化问题的求解方法与流程

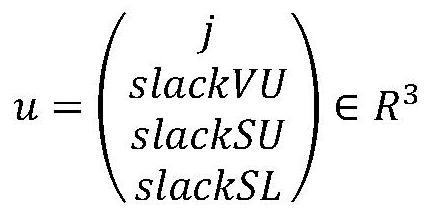
本发明涉及一种速度规划最优化问题的高性能求解方法，属于自动驾驶。

背景技术：

1、自动驾驶速度规划往往需要通过求解一类特殊的最优化问题来规划车辆在未来速度、加速度曲线，最典型的是将速度规划问题建模成一个二次规划(qudraticprogramming，qp)问题，并且利用通用的qp求解器(osqp)进行求解。

2、这类构建qp问题并用通用qp求解器求解的方法主要的缺陷是在于求解效率较低，难以求解细颗粒度，维度较高的问题。

技术实现思路

1、本发明所要解决的技术问题是，克服现有技术的缺点，提供一种速度规划最优问题的高性能求解方法，避免在线进行矩阵乘法和求逆运算，可以极大提升运算效率。

2、为了达到以上目的，本发明具体技术方案如下：一种速度规划最优问题的高性能求解方法，其特征在于：包括如下步骤，

3、步骤1，在速度规划模块，构建一个最优控制(optimal control problem，ocp)问题，并实时求解，将结果输出给下游控制模块进行执行，并定义速度规划的ocpqp问题

4、步骤2，利用经典的内点法(interior point method，ipm)对前述问题进行求解；根据标准的内点法求解步骤，最终可以收敛到最优解。

5、进一步的，所述步骤1中，首先取等间隔的规划的采样时间点：

6、t0＝0＜t1＜t2＜…＜tn＝t，

7、满足：ti＝iδt，其中t为规划的时间窗口，n为规划问题的离散化步数，δt＝t/n为规划的离散化时间步长；

8、定义最优控制问题的状态量：

9、

10、其中，s是自车沿着轨迹的位移，v是自车速度大小，a为自车的纵向加速度大小；

11、其次，定义最优控制问题的控制量为：

12、

13、其中，j为纵向加速度的变化率(加加速度)，有着明确的物理意义，而slackvu是速度软上界约束的松弛变量，slacksu是位移软上界约束的松弛变量，slacksl是位移软下界约束的松弛变量，通过软约束的添加可以提高模型求解的鲁棒性，减少求解失败的概率，并且可以极大提高求解的自适应性，可以根据业务需求开启某些软约束或者使得某些软约束不生效；

14、此时，优化变量为一个状态量序列和一个控制量序列：

15、

16、对优化的代价函数进行定义：

17、

18、其中：

19、

20、为代价函数中的拉格朗日代价(中间步代价)，

21、其中包含了对加速度和加加速度的惩罚项，保证行车的舒适平稳；而为对于前车的跟踪项，ki一般为指定的跟车时局，由业务需要实时输入模型，为对于前方车辆的速度跟踪项，最后三项为松弛变量的惩罚项，是对突破软约束的惩罚，另外：

22、

23、为终端代价；

24、进一步的，对定义模型进行约束：

25、首先建立动态递推关系：

26、xi+1＝axi+bui  (2)

27、其中：

28、

29、并且有当前的规划启点状态约束：

30、x0＝x*

31、并对如下的不等式约束，对对i＝0，....，n-1：

32、shardloweri≤si≤shardupperi

33、si≤ssoftupperi+slacksui

34、slacksui≥0

35、si≥ssoftloweri-slacksli

36、slacksli≥0

37、0≤vi≤vhardupperi

38、vi≤vsoftupperi+slackvui

39、slackvui≥0

40、ai≤ahardupperi

41、ai≥ahardloweri

42、其中第一个不等式是位移的上下界约束，而上下边界是根据实时的感知、预测、决策等上游模块输入信息计算得出；第二、第四个不等式是上下软边界约束，第六、第七个约束是速度软硬边界约束，用来进行对车速的限制，最后两个约束是车辆的加速度约束；

43、将上述10个不等式约束表示成更加紧凑的形式，令向量值函数c为：

44、

45、则上述不等式即为：

46、c(si，vi，ai，ui)≤0    (5)

47、由此将速度规划ocpqp问题表示为：

48、

49、s.t：

50、xi+1＝axi+bui

51、x0＝x*

52、c(si，vi，ai，ui)≤0，i＝0，...，n。

53、进一步的，计算lqr中的各矩阵及显示计算riccati迭代，最终以最大程度避免在线进行稠密矩阵的乘法运算和求逆矩阵运输以提高求解效率；具体包括如下内容：

54、构造lqr问题：

55、输入：x，u，λ，λ序列

56、输出：问题三中的各个矩阵

57、for i＝1，...，n：

58、

59、

60、

61、由此获得lqr各个系数矩阵的显示表达式，利用所述显示表达式可在线快速计算各个系数矩阵；

62、通用型riccati迭代：

63、输入：lqr问题的各个系数矩阵

64、输出：δx，δu序列

65、(1)反向迭代：

66、令稀疏矩阵：vxx，n＝hxx，n，vx＝rx，n

67、for i＝n-1，....，0：

68、令矩阵：

69、p＝vxx，i+1·bi+vx，i+1

70、quu，i＝huu，i+btvxx，i+1b

71、qxu，i＝hxu，i+atvxx，i+1b

72、qxx，i＝hxx，i+atvxx，i+1a

73、qu，i＝ru，i+btp

74、qx，i＝rx，i+atp

75、求逆矩阵继而求：

76、

77、

78、vxx，i＝qxx，i+qxu，i·ki

79、vx，i＝qx，i+qxu，i·ki

80、(2)前向迭代：

81、for i＝1，...，n：

82、δui-1＝ki-1δxi-1+ki-1

83、δxi＝aδxi-1+bδui-1+bi-1

84、λi-1＝-vxx，iδxi-vx，i。

85、进一步的，根据所述通用型riccati迭代算法可获得优化后的riccati迭代算法：

86、输入：lqr问题的各个系数矩阵

87、输出：δx，δu序列

88、(1)反向迭代：

89、令稀疏矩阵：vxx，n＝hxx，n，vx＝rx，n

90、for i＝n-1，....，0：

91、令quu，i为一个4x4的零矩阵，qxu，i为一个3x4的零矩阵，

92、qxx，i为一个3x3的零矩阵，且向这些矩阵里填入值：

93、ki为一个4x3的零矩阵，ki为一个3维列向量；

94、利用稀疏矩阵运算计算：

95、令稀疏矩阵：

96、m＝vxx，i+1·a，

97、n＝vxx，i+1·b

98、p＝vxx，i+1·bi+vx，i+1

99、计算qxx，i：

100、qxx，i(1，1)＝a(1，1)m(1，1)+hxx，i(1，1)

101、qxx，i(1，2)＝a(1，1)m(1，2)+hxx，i(1，2)

102、qxx，i(1，3)＝a(1，1)m(1，3)

103、qxx，i(2，2)＝a(1，2)m(1，2)+a(2，2)m(2，2)+hxx，i(2，2)

104、qxx，i(2，3)＝a(1，2)m(1，3)+a(2，2)m(2，3)

105、qxx，i(3，3)＝a(1，3)m(1，3)+a(2，3)m(2，3)+a(3，3)m(3，3)+hxx，i(3，3)

106、for j＝1，2，3：

107、for k＝1，..，j-1：

108、qxx，i(j，k)＝qxx，i(k，j)；

109、计算qxu，i：

110、qxu，i(1，1)＝a(1，1)n(1，1)

111、qxu，i(1，3)＝hxu，i(1，3)

112、qxu，i(1，4)＝hxu，i(1，4)

113、qxu，i(2，1)＝a(1，2)n(1，1)+a(2，2)n(2，1)

114、qxu，i(2，2)＝hxu，i(2，2)

115、qxu，i(3，1)＝a(1，3)n(1，1)+a(2，3)n(2，0)+a(3，3)n(3，1)

116、计算quu，i：

117、quu，i(1，1)＝b(1，1)n(1，1)+b(2，1)n(2，1)+b(3，1)n(3，1)+huu，i(1，1)

118、quu，i(2，2)＝huu，i(2，2)

119、quu，i(3，3)＝huu，i(3，3)

120、quu，i(4，4)＝huu，i(4，4)

121、计算

122、

123、计算ki：

124、for j＝1，..，3：

125、for k＝1，..，4：

126、ki(j，k)＝-quuinverse(j，j)qxu，i(k，j)

127、利用稀疏矩阵乘法计算：

128、qu，i＝ru，i+btp，qx，i＝rx，i+atp

129、计算ki：

130、forj＝1，...，4：

131、

132、计算vxx，i：

133、vxx，i(1，1)＝ki(1，1)qxu，i(1，1)+ki(3，1)qxu，i(1，3)+ki(4，1)qxu，i(1，4)+qxx，i(1，1)

134、vxx，i(1，2)＝ki(1，2)qxu，i(1，1)+qxx，i(1，2)

135、vxx，i(1，3)＝ki(1，3)qxu，i(1，1)+qxx，i(1，3)

136、vxx，i(2，2)＝ki(1，2)qxu，i(2，1)+ki(2，2)qxu，i(2，2)+qxx，i(2，2)

137、vxx，i(3，3)＝ki(1，3)qxu，i(3，0)+qxx，i(3，3)

138、for j＝1，.，3：

139、for k＝1，...，j-1：

140、vxx，i(j，k)＝vxx，i(k，j)

141、计算vx，i：

142、vx，i＝qx，i+qxu，i·ki

143、(2)前向迭代：

144、for i＝1，...，n：

145、δui-1＝ki-1δxi-1+ki-1

146、δxi＝aδxi-1+bδui-1+bi-1

147、λi-1＝-vxx，iδxi-vx，i。

148、进一步的，求解问题一最终优化后的算法：

149、输入：最大迭代次数maxiter

150、输出：问题一的求解结果，也就是规划的x，u序列；

151、3)取值μ＝1.0，初始化s，x，u等优化变量；

152、4)对i＝0，1，...，maxiter-1：

153、2.1)按照算法三构造问题三中的lqr问题；

154、2.2)利用算法四求解lqr问题，并且利用公式(10)(11)得到迭代步：

155、δxi，δui，δλi，δλi，δsi

156、2.3)计算合适的迭代步长α，并且更新x，u，s：

157、xi+＝αδxi

158、ui+＝αδui

159、si+＝αδsi

160、λi+＝αδλi

161、λi+＝αδλi

162、2.4)如果kkt条件(7)在一定误差范围内满足，停止，

163、否则更新：μ＝0.5μ，继续迭代。

164、与现有技术相比，本发明的有益效果为：

165、1.本发明用内点法将速度规划的ocpqp问题转化为一系列的可以快速求解的lqr问题，算法的时间复杂度达到o(n)，明显优于开源的通用qp求解器osqp，qpoases等(关于n是2次方或者3次方的时间复杂度)。

166、2.针对具体问题在线显式计算lqr问题的各个矩阵，显示计算riccati迭代中的各个矩阵，避免了在线计算矩阵乘法，极大提高了运行的效率。

167、3.对于需要在线求逆的矩，论证其为一个对角矩阵，可以显式在线求逆，避免了对通用矩阵的在线求逆计算，提高运行效率。

168、4.对于对称矩阵只计算出上三角部分的各个值，可以节省约一半的算力。