一种基于微分平坦的固定翼无人机轨迹规划方法

本发明涉及一种基于微分平坦的固定翼无人机的轨迹规划方法，属于飞行器的轨迹规划领域。

背景技术：

1、固定翼无人机具备飞行航程长、高空飞行能力等优点，能够高效完成搜救、覆盖侦察和环境观测等飞行任务，受到了各国航空领域的广泛研究。作为固定翼无人机的自主智能化的关键技术之一，轨迹规划能够为复杂的飞行任务生成平滑、动态精确且安全避碰的运动轨迹，在固定翼无人机的自主应用中发挥着至关重要的作用。然而，与无人直升机、多旋翼机和其他飞行平台相比，固定翼飞行器的轨迹规划存在非完整动力学的强非线性(例如，最小飞行速度、有界转弯曲率和耦合控制通道)，这使得在轨迹规划过程中难以实现快速收敛。因此，固定翼无人机实现的轨迹高效规划仍然面临具大的挑战。

2、近年来，固定翼无人机的轨迹规划技术受到国内外学者的广泛关注，并取得了一定的理论研究成果。然而，现有方法或者直接简化、线性化固定翼的动力学模型，仅考虑运动学约束导致生成的轨迹精度低，难以满足日益复杂的飞行任务需求；采用gpops-ii、acado等通用轨迹规划工具包直接求解含有复杂动力学约束的轨迹规划问题，求解耗时过长，无法满足在线轨迹规划任务需求。因此，有必要针对固定翼无人机的动力学特性，基于微分平坦原理建立固定翼无人机的轨迹表征模型，消去轨迹规划问题中的动力学约束，并通过设计积分型罚函数性能指标，处理轨迹规划问题中的不等式约束，将原轨迹规划问题转换为具有较低求解复杂度的无约束轨迹规划问题，实现固定翼无人机轨迹规划的快速求解，保证固定翼无人机在复杂障碍物环境下飞行任务的快速、安全任务需求。

技术实现思路

1、本发明的主要目的是提供一种基于微分平坦的固定翼无人机的轨迹规划方法，针对固定翼无人机的轨迹规划问题面临的计算高耗时问题，通过建立基于微分平坦的的轨迹表征模型，消去轨迹规划问题中的等式约束；利用基于微分平坦的轨迹表征模型，通过设计积分型罚函数性能指标处理轨迹规划问题中的不等式约束，将原轨迹规划问题转换为解析梯度的无约束轨迹规划问题，从而降低轨迹规划问题的求解复杂度，实现固定翼无人机轨迹规划的快速求解，保证固定翼无人机在复杂障碍物环境下飞行任务的快速、安全任务需求。

2、本发明的目的是通过如下技术方案实现的。

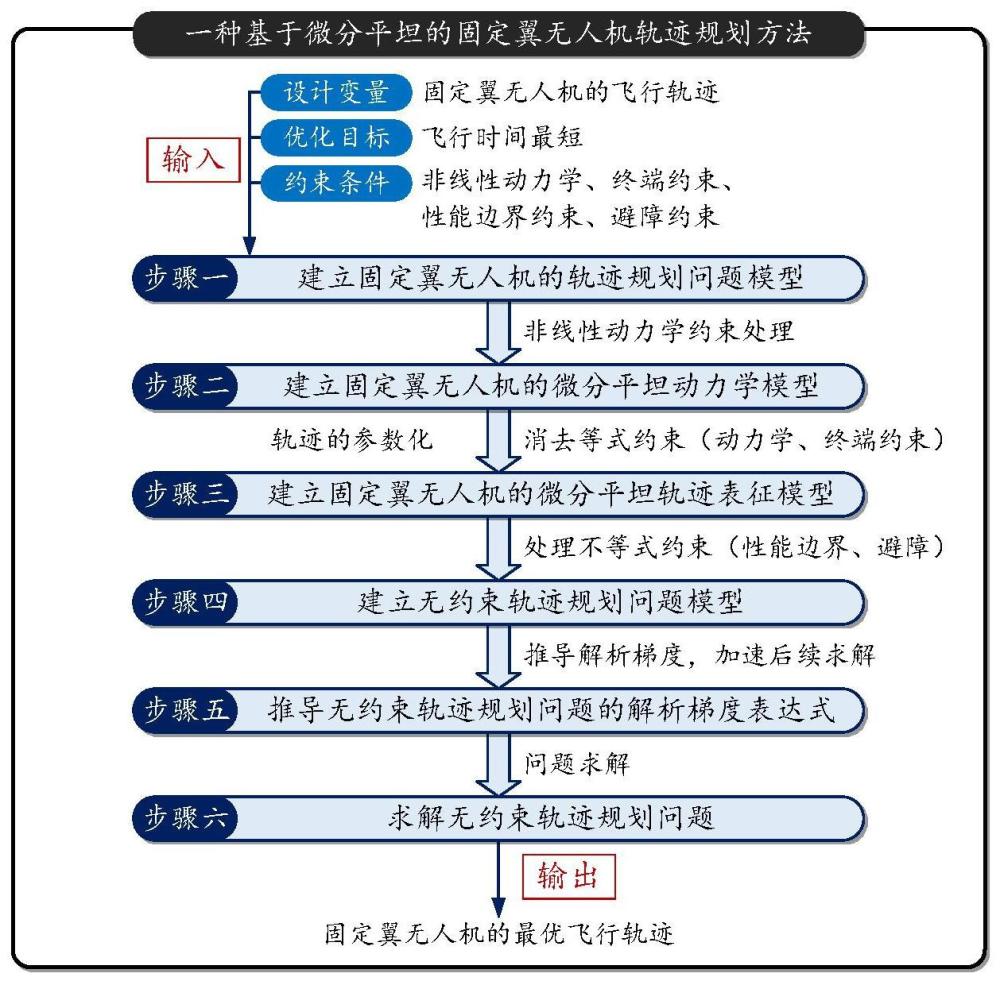
3、考虑固定翼无人机的非线性动力学约束、终端约束、性能边界约束和避障约束，以飞行时间最短为目标函数，建立固定翼无人机的轨迹规划问题模型；针对非线性动力学约束，基于微分平坦理论进行精确线性化，建立固定翼无人机的微分平坦动力学模型；采用样条曲线参数化飞行轨迹，建立基于微分平坦的轨迹表征模型，消去轨迹规划问题中的等式约束；利用基于微分平坦的轨迹表征模型，通过设计积分型罚函数性能指标处理轨迹规划问题中的不等式约束，将原轨迹规划问题转换为无约束轨迹规划问题，并支持推导目标函数的解析梯度提升求解效率，实现固定翼无人机轨迹规划的快速规划。

4、本发明公开一种基于微分平坦的固定翼无人机的轨迹规划方法，包括以下步骤：

5、步骤一、考虑固定翼无人机的非线性动力学约束、终端约束、性能边界约束和避障约束，以飞行时间最短为目标函数，建立固定翼无人机的轨迹规划问题模型：

6、

7、式中：t为时间，状态变量x(t)＝[x(t),y(t),z(t),v(t),χ(t),γ(t)]t包含固定翼无人机的三维位置坐标x(t)、y(t)、z(t)，飞行速度v(t)，航向角χ(t)和轨迹倾角γ(t)，控制变量u(t)＝[nx(t),ny(t),nz(t)]t包含固定翼无人机的切向过载nx(t)、横向过载ny(t)和法向过载nz(t)；式(1-a)代表轨迹规划的目标函数，其中，t0为起始时刻，tf为终端时刻，为目标函数，即最小化飞行时间tf-t0；式(1-b)～(1-e)代表轨迹规划的约束条件，其中：式(1-b)为固定翼无人机的非线性动力学约束，上标·代表变量对时间的一阶导数；式(1-c)为终端约束，x0和u0分别代表t0时刻的状态向量和控制向量值，xf和uf分别代表tf时刻的状态向量和控制向量值；式(1-d)为固定翼无人机的性能边界约束，其中xmin≤x(t)≤xmax代表状态变量的边界约束，umin≤u(t)≤umax代表控制变量的边界约束，下标(·)max和(·)min分别代表对应变量的上下边界值；式(1-e)代表避障约束，其中代表障碍物集合，pobs,j是第j个障碍物的二维位置坐标，robs,j是第j个障碍物的半径，rsafe是无人机到障碍物的最小安全距离，g＝[i2×2,04×4]为二维坐标选择矩阵，其中，i2×2为2×2的单位矩阵，04×4为4×4的零矩阵；式(1-b)具体表示为：

8、

9、式中，g为重力加速度；式(1-c)具体表示为：

10、

11、其中：(3-a)为飞行速度的边界约束，(3-b)为轨迹倾角的边界约束，(3-c)～(3-e)分别代表切向过载、横向过载和法向过载的边界约束；

12、为简便描述，将x(t)、u(t)、x(t)、y(t)、z(t)、v(t)、χ(t)、γ(t)、nx(t)、ny(t)、nz(t)分别简记为x、u、x、y、z、v、χ、γ、nx、ny、nz；

13、步骤二、针对步骤一中的固定翼无人机的非线性动力学约束，基于微分平坦原理，通过定义微分平坦输出及微分平坦映射，将非线性动力学约束进行精确线性化，建立固定翼无人机的微分平坦动力学模型；

14、针对步骤一中的式(2)，基于微分平坦原理，选择位置向量p＝[x,y,z]t为微分平坦输出，定义状态向量的微分平坦映射和控制向量的微分平坦映射如式(4)所示：

15、

16、式中：上标t为矩阵转置符号；e1＝[1,0,0]t、e2＝[0,1,0]t、e3＝[0,0,1]t为惯性坐标系三轴的单位方向向量；为速度向量，||·||代表向量的二范数；arctan2(·)是四象限反正切函数，arcsin(·)是反正弦函数；r1＝v/||v||，r2＝(e3×v)/||e3×v||，r3＝v×(e3×v)/||v×(e3×v)||为速度坐标系三轴的单位方向向量，其中，×为向量的叉乘符号；和的逆映射和具体如式(5)所示：

17、

18、式中为加速度向量；根据式(4)～(5)中描述的映射关系，可以将式(2)精确线性化为式(6)：

19、

20、式(4)～(6)即为固定翼无人机的微分平坦动力学模型；

21、步骤三、针对步骤二中的固定翼无人机的微分平坦动力学模型，采用样条曲线对微分平坦输出进行参数化，建立基于微分平坦的固定翼无人机的轨迹表征模型，消去步骤一得到的轨迹规划问题中的动力学约束和终端约束；

22、采用如式(7)所示的n段连续的多项式样条对p进行参数化：

23、

24、式中：代表第i段多项式样条，b(τ)＝[1,τ,τ2,...,τs-1]t为s-1阶的多项式基函数，ci为第i段多项式样条的系数矩阵，大小为s×3；τ为t在[ti,ti-1]区间的归一化时间，其中ti-1、ti代表第i段多项式样条的起始和终端时刻，记ti＝ti-ti-1为第i段多项式样条的时间长度；p的n阶时间导数如下：

25、

26、其中，dnp/dtn代表p对时间t的n阶导数，dnb/dτn代表b(τ)对归一化时间τ的n阶导数；为简化描述，后续将dnp/dtn简记为p(4),...,p(n)，b(τ)简记为b，dnb/dτn简记为b(4),...,b(n)；

27、在t＝t0和t＝tf时刻，p在满足式(9)所示的终端约束，即：

28、

29、其中，p0、v0、a0分别为位置、速度、加速度向量在初始时刻的约束值，pf、vf和af分别为位置、速度、加速度向量在终端时刻的约束值，b(0)、分别代表τ＝0时的b及其1～2阶导数，b(1)、分别代表τ＝1时的b及其1～2阶导数；此外，对于任意两段相邻的多项式样条i和i+1，在衔接时刻t＝ti，满足如下的连续性约束：

30、

31、式中，pi为衔接点的位置坐标；记t＝tf-t0为总飞行时间，设每段多项式样条具有相同的时间长度，即ti＝t/n,式(9)～(10)可以总结为如下形式：

32、

33、其中：为常值矩阵；代表ci的矩阵排列；代表边值约束矩阵；记为pi的矩阵排列，是由和t决定的；式中(11)的矩阵和具体如下：

34、

35、其中：

36、

37、其中，b(0)、b(4)(0)分别代表τ＝0时的b及其1～4阶导数，b(1)、b(4)(1)分别代表τ＝1时的b及其1～4阶导数；是一个非奇异的常值矩阵，因此，可由式(14)计算得出：

38、

39、综合式(7)～(14)，得到固定翼无人机的多项式轨迹表征模型trajfw如式(15)所示：

40、

41、其中，状态和控制向量x和u由和飞行总时长t紧实参数化：当确定和t之后，通过式(14)确定进一步通过式(7)～(8)计算p及因为再通过式(4)计算x和u的值；基于trajfw，消去式(1)中的非线性动力学约束(1-b)和终端约束(1-c)，改写为如式(16)所示的形式：

42、

43、式中，固定翼无人机的状态向量x和控制向量u由和t决定；式(16-b)的形式与(1-d)相同，具体形式如式(3)所示；式(16-c)的形式与(1-e)相同；通过式(16)可知，仅需要求解和t即可间接计算固定翼无人机的x和u，避免了轨迹规划中的非线性动力学约束和终端约束导致的计算负担，从而能够提升轨迹规划的求解效率；

44、步骤四、通过设计积分型罚函数性能指标处理式(16)中的不等式约束(16-b)、(16-c)，将轨迹规划问题进一步转换为式(17)所示的无约束轨迹规划问题模型：

45、

46、式中，代表积分型罚函数性能指标，由和t决定；的下标索引σ∈{obs,v,γ,nx,ny,nz}，即具体包含：避障约束的积分型罚函数指标速度约束的积分型罚函数指标轨迹约束的积分型罚函数指标以及切向、法向和横向过载约束的积分型罚函数指标λσ为各对应的权重系数；

47、计算需要对每一段轨迹上的性能指标值进行积分并求和，采用式(18)所示的梯形积分进行近似计算：

48、

49、式中，是第i段轨迹的性能指标值，tk＝kt/nκ,k＝＝0,1,2,...,κ为采样时刻，κ为采样点数；ωk为梯形积分权重，当k＝0或κ时，ωk＝1/2，其余情况ωk＝1；为对应的被积罚函数，下标索引σ∈{obs,v,γ,nx,ny,nz}，即具体包含：避障约束的被积罚函数速度约束的被积罚函数轨迹约束的被积罚函数以及切向、法向和横向过载约束的被积罚函数

50、被积罚函数具体为：

51、

52、式中，为幂指数，max[φσ,0]为取φσ和0的最大值；φσ为待设计的函数，下标索引σ∈{obs,v,γ,nx,ny,nz}，φσ由ci和t决定；

53、式(17)是一个无约束优化问题，相比式(1)所示的有约束优化问题具有更低的求解复杂度，因此求解式(17)能够更快速的计算固定翼无人机的飞行轨迹；

54、步骤五、针对步骤四中的无约束轨迹规划问题模型，推导其解析梯度表达式；

55、式(17)中的目标函数可以表述为以下泛函形式：

56、

57、式中：是和t的泛函；是和t的泛函，对应式(17)的等式右侧；θ＝diag{θ(t/n),...,θ(t/n)}是6n×6n的对角矩阵，其对角由θ(t/n)排列，θ(t/n)＝diag{1,n/t,n2/t2,...,n5/t5}为6×6矩阵，θ仅由t的决定；而由式(14)可知，由和t决定；分别对式(20)左右两端关于和t求偏导，可得：

58、

59、式中：col{·}代表元素的按列进行排列；δ＝[1,0,0,0,0,0]t为常值列向量；矩阵g1～gn-1根据计算；tr{·}代表矩阵的迹运算；θ-1是矩阵θ的逆；式(21)即为由和间接计算目标函数的梯度值和的解析表达式；通过式(21)所示的解析表达式计算目标函数梯度值进行优化迭代，能够避免有限差分频繁迭代计算梯度值带来的计算负担，因此能够缩短规划耗时，提升轨迹规划的求解效率；

60、步骤六、针对步骤四中式(17)所示的无约束轨迹规划问题模型，利用步骤五推导的解析梯度表达式加速优化求解，实现固定翼无人机飞行轨迹的快速规划；首先，设置任务想定，包含固定翼无人机的性能边界约束值、终端约束值和障碍物信息；其次，设置算法参数；然后，生成固定翼无人机的初始轨迹；基于该初始轨迹，计算目标函数值，并利用解析梯度公式计算梯度值，然后采用l-bfgs算法进行优化迭代；不断循环迭代轨迹，直至满足收敛条件，输出规划结果，满足固定翼无人机在复杂障碍物环境下飞行任务的快速、安全任务需求；具体步骤如下：

61、步骤6.1：轨迹规划的想定设置；设置固定翼无人机的性能边界约束值xmax、xmin、umax、umin和终端约束值x0、u0、xf、uf，并给定障碍物集合包含信息pobs,j、robs,j，

62、步骤6.2：算法参数设置；设置算法参数，包括：n、κ、λσ、ζσ和rsafe；

63、步骤6.3：初始轨迹生成；采用三维dubins路径生成轨迹规划的初值，用三维dubins连接终端状态x0、xf，将生成的路径等距分割为n段，其衔接点作为的初值，记作并用三维dubins路径的长度除以最大速度vmax，作为t的初值，记作t0，利用根据式(15)生成固定翼无人机的初始轨迹x0、u0，其中上标0代表是变量的初始值；置q＝0；

64、步骤6.4：计算目标函数值及其梯度值；记上标q代表各变量在第q次迭代的值，根据tq，通过式(14)可以确定多项式系数矩阵进一步通过式(7)～(8)计算pq及最后利用式(4)计算状态向量和控制向量xq和uq；然后，根据式(17)计算目标函数值根据式(21)利用链式法则计算和将和按列排列，记作和即为第q次迭代的目标函数及其梯度值；

65、步骤6.5：检测是否满足收敛性条件；如果xq、uq满足避障约束和性能约束，并且满足ε为收敛容差，||·||代表向量的二范数，则判定轨迹规划满足收敛条件，跳转至步骤6.7；否则，执行步骤6.6；

66、步骤6.6：采用基于梯度的优化算法进行迭代；考虑固定翼无人机轨迹规划的时效性需求，作为优选，采用l-bfgs算法利用梯度值进行优化迭代，得到下一次迭代的tq+1，置q＝q+1；然后转至步骤6.4；

67、步骤6.7：规划结果输出；令x*＝xq，u*＝uq，t*＝tq；x*和u*即为固定翼无人机的最优飞行轨迹对应的状态向量和控制向量值，t*即为最短飞行时间；

68、通过上述步骤，能够快速规划满足固定翼无人机非线性动力学约束、终端约束、性能边界约束和避障约束的最优飞行轨迹，满足固定翼无人机的安全、快速执行飞行任务需求。

69、进一步地，步骤四所述φσ为待设计的函数，由φobs、φv、φγ、构成，由ci和t确定；

70、φσ的设计过程具体实现方法如下：

71、步骤4.1：为保证固定翼无人机在飞行过程中的安全避障，针对式(16-c)中描述的避障约束，设计如下的φobs：

72、

73、式中，φobs,j是对第j个障碍物的代价函数值，ζobs＞1为收缩系数，为二维坐标选择矩阵；在轨迹规划过程中，当无人机距离障碍物j过近时，φobs,j的数值将为正，会驱使无人机远离障碍物，直到满足避障约束；

74、步骤4.2：为满足式(3-a)中速度的边界约束vmin≤v≤vmax，设计如下的φv：

75、

76、式中，vc＝(vmax+vmin)/2，vh＝(vmax-vmin)/2，ζv＜1为收缩系数；在轨迹规划过程中，当无人机的飞行速度超出限制时，φv的数值将为正，会驱使速度改变直至满足约束；

77、步骤4.3：针对式(3-b)中的轨迹倾角的边界约束γmin≤γ≤γmax，考虑到sin(·)在[-π/2,π/2]区间的单调递增性，将轨迹倾角约束等价为sinγmin≤sinγ≤sinγmax，然后设计如下的φγ：

78、

79、式中，γc＝(sinγmax+sinγmin)/2，γh＝(sinγmax-sinγmin)/2，ζγ＜1为收缩系数；在轨迹规划过程中，当无人机的航迹倾角超出限制时，φγ的数值将为正，会驱使航迹倾角满足约束；

80、步骤4.4：针对式(3-c)～(3-e)中的切向过载约束nx,min≤nx≤nx,max、横向过载约束ny,min≤ny≤ny,max和法向过载约束nz,min≤nz≤nz,max，设计为简便描述，将统一记为为nx、ny、nz的下标索引，设计如(25)所示的

81、

82、式中，nl,c＝(nl,max+nl,min)/2，nl,h＝(nl,max-nl,min)/2，为对应的收缩系数；在轨迹规划过程中，当无人机的过载超处限制时，的数值将为正，驱使满足过载约束。

83、进一步地，步骤五中式(21)通过下述方法解算得到：

84、步骤5.1：式(21)中的和可以由式(26)计算为：

85、

86、步骤5.2：推导对和t的偏导数；对式(17)右端关于和t求偏导，可得式(21)中具体为：

87、

88、式中：下标索引σ∈{obs,v,γ,nx,ny,nz}，和分别为对和t的偏导数，具体为

89、

90、式中：col{·}代表元素的按列进行排列；和为第i段轨迹上的性能指标对相应的多项式系数矩阵ci和t的导数，由式(18)可得：

91、

92、通过计算再通过式(27)～(29)逐步带入，即可得到和

93、结合式(22)～(25)可知，和包含φobs、φv、φγ和分别对ci和t的偏导数，具体为：

94、(1)φobs对ci和t的偏导数为：

95、

96、(2)φv对ci和t的偏导数为：

97、

98、(3)φγ对ci和t的偏导数为：

99、

100、(4)对ci和t的偏导数具体为：

101、

102、式中：

103、

104、其中，i为3×3单位矩阵；w2＝e3×v和w3＝v×(e3×v)为中间变量；[e3]×＝[0,-1,0；1,0,0；0,0,0]为e3向量的叉乘矩阵；

105、步骤5.3：在完成步骤5.1和5.2后，将和带入式(21)，利用链式法则，即可以获得目标函数的对和t的梯度和将和按列排列，记作即为目标函数的解析梯度表达式。

106、有益效果：

107、1、本发明公开一种基于微分平坦的固定翼无人机轨迹规划方法，针对固定翼无人机的轨迹规划中的非线性动力学约束，通过固定翼无人机的微分平坦动力学推导，通过样条曲线的参数化，建立基于微分平坦的轨迹表征模型，该表征模型消去了轨迹规划问题中的等式约束，能够避免轨迹规划中的非线性动力学导致的计算负担，提升轨迹规划的求解效率。

108、2、本发明公开一种基于微分平坦的固定翼无人机轨迹规划方法，考虑固定翼无人机的非线性动力学约束、终端约束、性能边界约束和避障约束，以飞行时间最短为目标函数，利用基于微分平坦的轨迹表征模型，通过设计积分型罚函数性能指标处理轨迹规划问题中的不等式约束，并推导目标函数的解析梯度，将原轨迹规划问题转换为梯度解析的无约束轨迹规划问题，能够实现固定翼无人机轨迹规划的快速求解，保证固定翼无人机在复杂障碍物环境下飞行任务的实时性、安全性需求。