一种盲校准的单目标估计场景的牛顿正交匹配检测方法与流程

本发明属于水声信号处理领域，具体是涉及一种盲校准的单目标估计场景的牛顿正交匹配检测方法。

背景技术：

1、多种应用(比如波束成形或者到达方向估计)中传感器阵列实现准确操作的一个显而易见的要求就是准确地校准它们的组成元素，不幸的是，由于实际情况中存在的困难(比如接收器的温度变化或者频率漂移)，模型参数经常会发生错误，比如传感器的增益和相位的相对变化，这将恶化估计表现。尽管离线的校准(也就是说先于操作流程，尽可能在已知的位置使用已知的校准信号)是相对简单的，但实际上，自校准或者盲校准仍然是一个非常有挑战性的工作。

2、盲校准在很多应用中的整体成功操作中扮演着一个重要的角色，比如说，对pushbroom摄像机来说，由于设备内部的传感器与传感器间的变化经常会导致图像有条纹，一些学者们提出了盲校准方法作为柱状图(histogram)匹配的替代方法。在声学传感器阵列中，当信号源和接收传感器的位置不是已知的先验信息的时候(a-priori)，盲校准就显得尤为重要。此外，盲校准问题也广泛应用于环境传感器网络，射电天文学，基于压缩感知的成像传感器等。

3、对于未知的传感器的增益和相位，paulraj和kailath提出了一种最小二乘方法；为了联合估计阵列和到达方向角度，friedlander和weiss提出了一种特征值方法；chong和see提出了一种直接的最大似然方法，其中最大似然估计是通过一种迭代算法求解的，但是未必总是收敛。针对均匀线性阵列，有学者提出了一种最大似然-最佳加权最小二乘盲校准方法，输入观测数据，输出校准后的数据，估计角度、幅度和相位的响应误差。具体地：

4、计算观测数据的协方差矩阵；基于上一步的协方差矩阵，通过公式计算得到一个加权的估计误差协方差矩阵的最大似然估计值；利用公式构建一个相关性测量模型；通过公式得到最大似然-最佳加权最小二乘估计结果；进而得到幅度和相位的最大似然-最佳加权最小二乘估计结果；最终输出校准后的数据；但是这些方法都是有启发性，但不是最优的。

5、因此，传统的算法只能通过先于操作流程，尽可能在已知的位置使用已知的校准信号，难以处理自校准或者盲校准问题。而一些针对盲校准的算法普遍存在收敛性低、复杂度高、精度低等问题，不是最优的。比如直接的最大似然方法，联合估计所有的未知的模型参数，导致了一个多维的优化问题，没有闭式表达式，且不是每次都收敛。

技术实现思路

1、基于现有技术的不足，本发明的目的是提供一种复杂度低、精度高、可减轻格点错配、渐进最优的求解基于单目标盲校准问题的一种牛顿正交匹配追踪算法。

2、本发明的技术方案为：

3、一种盲校准的单目标估计场景的牛顿正交匹配检测方法，包括如下步骤：

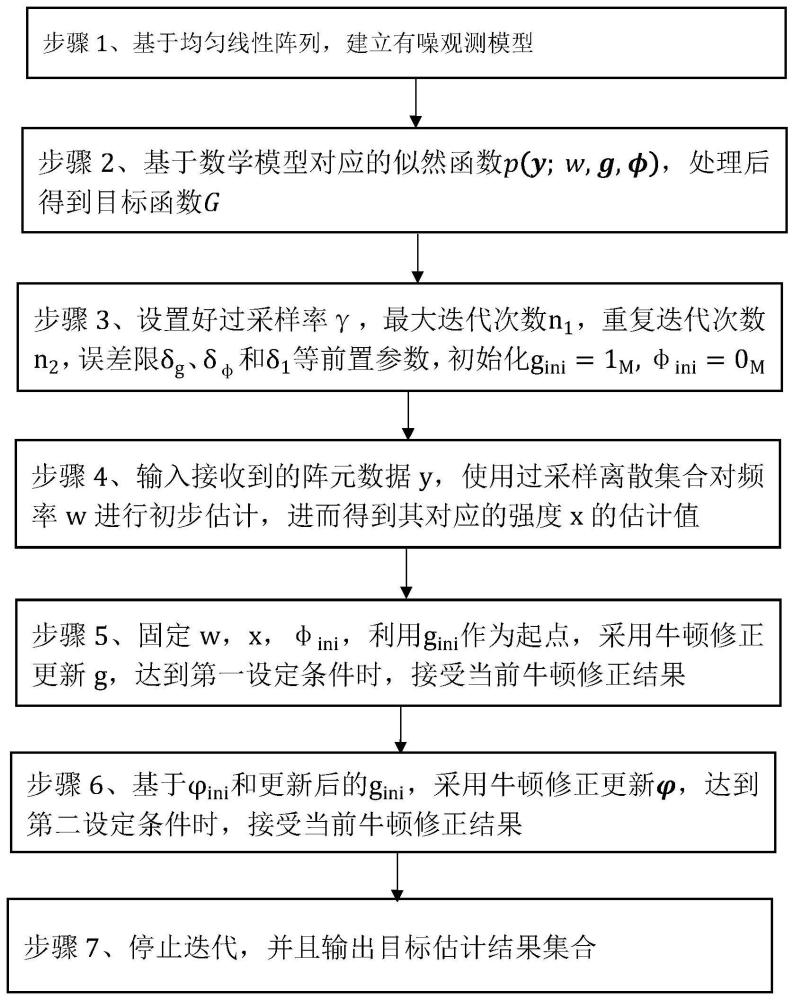
4、步骤1、基于均匀线性阵列，建立有噪观测模型；

5、步骤2、基于数学模型对应的似然函数p(y；w，g，φ)，处理后得到目标函数g；

6、步骤3、设置好过采样率γ，最大迭代次数n1，重复迭代次数n2，误差限δg、和δ1等前置参数，设g＝1m×1，初始化

7、步骤4、输入接收到的阵元数据y，使用过采样离散集合对频率w进行初步估计，进而得到其对应的强度x的估计值；

8、步骤5、固定w，x，利用gini作为起点，采用牛顿修正更新g，达到第一设定条件时，接受当前牛顿修正结果；

9、步骤6、基于和更新后的gini，采用牛顿修正更新达到第二设定条件时，接受当前牛顿修正结果；

10、步骤7、停止迭代，并且输出目标估计结果集合。

11、优选地，所述步骤1中，基于一个均匀线性阵列ula，将有噪观测模型建模为

12、y＝diag(g)diag(p)(ax+u)+v＝diag(g)diag(p)ax+diag(g)diag(p)u+v.

13、其中y∈cm×1表示有噪观测，c表示复数集合，

14、m表示传感器的数量，x表示强度，u和v为两个噪声矢量，diag(g)表示一个对角线元素为g对应的每一个元素，其他位置数值为0的方阵，

15、

16、表示幅度抵消量，p∈cm×1表示相位抵消量，r+表示正实数，p的每一个元素表示相位；

17、频率d表示阵元间距，λ表示波长，θ表示方位角。

18、优选地，所述步骤1中，对于频率取则有w＝πsinθ；

19、通过定义w＝diag(g)diag(p)u+v.

20、则有这里的σ2表示噪声方差，g2表示对g的每一个元素取平方，cn表示复高斯分布，im表示一个阶数为m，对角线元素为1，其他元素为0的方阵；

21、约束为(δ表示一个数值较小的量)；

22、gm∈[1-δg，1+δg]，m＝1，…，m。

23、优选地，所述步骤2中，步骤1数学模型对应的似然函数为：

24、

25、其中，||表示取绝对值，

26、对观测的似然函数的每一项取对数，则有：

27、

28、最小化目标函数：

29、

30、其中，

31、优选地，所述步骤4中，通过在0到2π范围内按照过采样率γ设置过采样网格，得到了γm个格点频率，使用有限离散集合代替无限集合通过最大化罚函数来得到线谱频率w的估计值，进而得到其对应的强度x的估计值。

32、优选地，所述步骤5中，基于更新后的gini，采用牛顿修正更新g，即

33、

34、

35、

36、

37、优选地，所述步骤5中，接受牛顿修正的第一设定条件为：

38、如下三个子条件同时成立：

39、a、g的汉森矩阵的行列式的值大于0；

40、b、更新后的g对应的罚函数的值小于更新前的g对应的值；

41、c、更新后的g的每一个分量全部位于(1-δg，1+δg)。

42、优选地，所述步骤6中，基于更新后的采用牛顿修正更新即

43、

44、

45、

46、im表示取虚部操作，re表示取实部操作。

47、优选地，所述步骤6中，接受牛顿修正的第二设定条件为：

48、如下三个子条件同时成立：

49、a、的汉森矩阵的行列式的值大于0；

50、b、更新后的对应的罚函数的值小于更新前的对应的值；

51、c、更新后的的每一个分量全部位于

52、优选地，所述步骤5、步骤6中，在满足如下两个条件之一时，

53、a、迭代次数n1达到上限；

54、b、更新前后的g和的差的绝对值小于δ1的次数达到n2次；

55、停止迭代，并且输出目标估计结果集合。

56、本发明的有益效果为：

57、1、本发明使用牛顿梯度下降法对幅度抵消量和相位抵消量进行估计，有效减轻了格点错配问题带来的影响，提高了频率估计精度；

58、2、本发明利用快速傅里叶变换的优势，彻底避免了矩阵求逆的操作，计算复杂度得以大幅度降低，便于芯片实现；

59、3、本发明可联合估计频率、强度、幅度抵消量和相位抵消量。