宽带信号多频带联合稀疏贝叶斯学习的波达方向估计方法

本发明属于雷达，具体涉及宽带信号多频带联合稀疏贝叶斯学习的波达方向估计方法。

背景技术：

1、随着现代科技的快速发展，雷达和通信系统的信号形式越来越多样化，信号环境日益复杂，占据的信号带宽也越来越宽，比如通信中经常使用的扩频信号、跳频信号、线性调频等信号，还有自然界中的声音信号、地震波等都属于宽带信号。

2、波达方向估计技术是实现目标定位不可或缺的技术手段，通过波达方向估计结果可获得目标在空域的方位信息。宽带信号波达方向估计技术中一种典型的处理方式是频域处理法，将阵列接收数据通过离散傅里叶变换得到各子频带的数据，再用非相干信号子空间法或相干信号子空间法进行后处理。

3、稀疏贝叶斯学习是贝叶斯统计优化的一个重要组成部分，主要是基于贝叶斯推断提出的，凭借其优秀的稀疏重构性能在阵列信号处理等领域得到广泛应用。稀疏贝叶斯学习技术通常将待估计的参数看成符合某种先验分布的变量，凭借已有知识确定先验分布的形式，利用贝叶斯推断来计算未知参数的后验概率，从而做出相应的推断。但将稀疏贝叶斯学习理论引入宽带信号doa估计中存在两个问题，1)如何实现多频带的联合估计；2)如何有效降低宽带信号多快拍多频带下的计算复杂度。

技术实现思路

1、本发明的目的是提供宽带信号多频带联合稀疏贝叶斯学习的波达方向估计方法，以实现高分辨率、高精度、低计算复杂度的宽带信号波达方向估计性能。

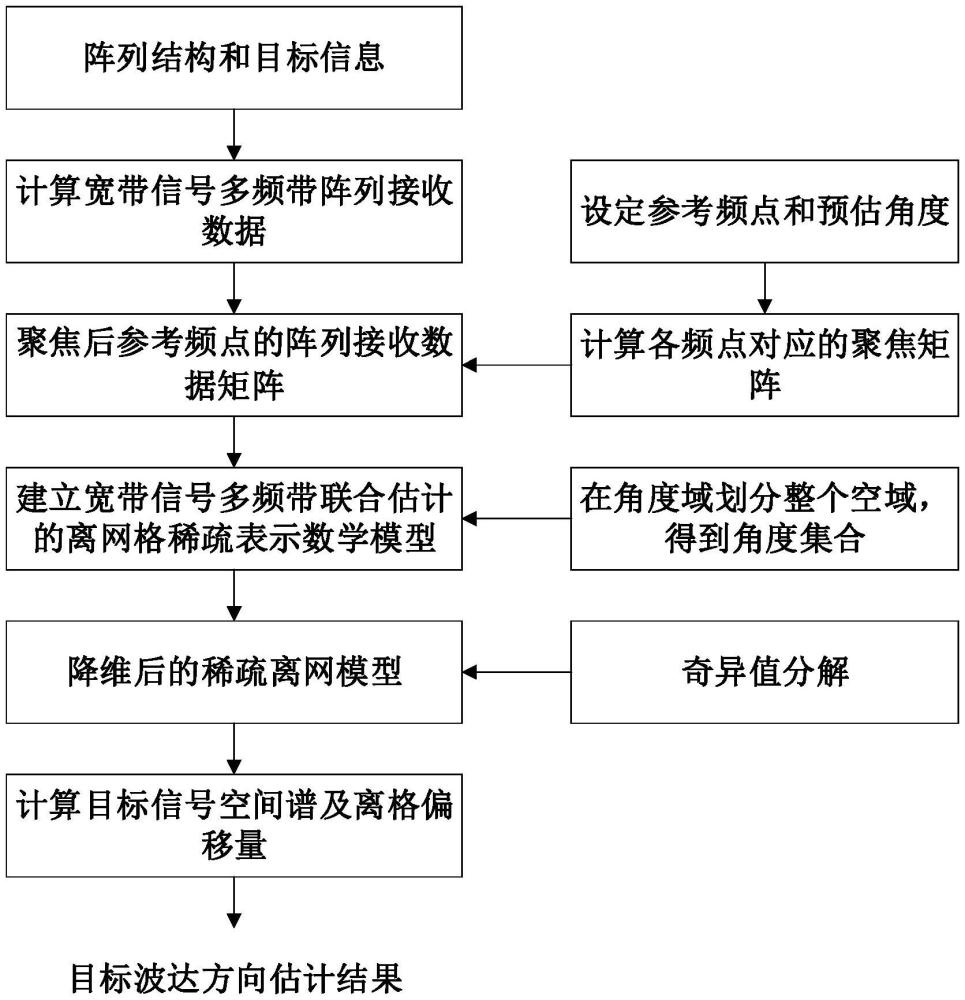
2、本发明所采用的技术方案是，宽带信号多频带联合稀疏贝叶斯学习的波达方向估计方法，具体按照以下步骤实施：

3、步骤1、根据相控阵雷达的阵列结构及空域目标信息，计算宽带信号多频带的阵列接收数据矩阵；

4、步骤2、根据步骤1得到的宽带信号多频带阵列接收数据矩阵，计算聚焦后参考频点的阵列接收数据矩阵；

5、步骤3、根据步骤2得到的参考频点阵列接收数据矩阵和稀疏表示理论，建立宽带信号多频带联合估计的离网格稀疏表示数学模型；

6、步骤4、对步骤3得到的数学模型进行奇异值分解，得到降维后的稀疏重构模型；

7、步骤5、根据稀疏贝叶斯理论求解步骤4得到的降维后稀疏重构模型，得到目标信号的空间谱及离格偏移量；

8、步骤6、根据步骤5得到的目标信号的空间谱和离格偏移量，计算宽带信号波达方向估计结果。

9、本发明的特点还在于，

10、步骤1具体按照以下步骤实施：

11、步骤1.1、根据相控阵雷达的阵列结构及空域目标信息，计算第m个阵元接收的回波信号rm(t)：

12、

13、其中，sk(t)表示k个宽带信号，θk表示第k个信号的来波方向，k＝1,2,…,k，k表示目标个数，τm(θk)＝mdsinθk/c表示信号sk(t)到达第m个阵元相对于参考阵元的时延差，m＝1,2,…,m，m表示阵元数，c是电磁波传播速度，d为阵元间距，nm(t)为第m个阵元上的高斯白噪声，均值为0，方差为

14、步骤1.2、对步骤1.1得到的阵列回波信号进行离散傅里叶变换，得到频率fj点的阵列数学模型为：

15、r(fj)＝a(fj,θ)s(fj)+n(fj),j＝1,…,j

16、其中，r(fj)＝[r1(fj),r2(fj),…,rm(fj)]t，s(fj)＝[s1(fj),s2(fj),…,sk(fj)]t和n(fj)＝[n1(fj),n2(fj),…,nm(fj)]t分别为频率fj点的阵列回波信号、目标信号和噪声的离散傅里叶变换，假设噪声服从高斯分布，并且各个子频带的噪声相互独立，j＝1,…,j，j表示子频带个数，(·)t表示转置运算。θ＝[θ1,θ2,…,θk]，a(fj,θ)为频率fj点的m×k维的阵列流型矩阵，a(fj,θ)＝[a(fj,θ1),a(fj,θ2),…,a(fj,θk)]∈cm×k，a(fj,θk)为导向矢量，

17、步骤1.3、根据步骤1.2得到的频率fj点的阵列数学模型及矩阵论知识，得到宽带信号多频带的阵列接收数据矩阵：

18、

19、步骤2具体按照以下步骤实施：

20、步骤2.1、选择宽带信号在频域的第一个频点f1作为参考频点f0；

21、步骤2.2、设定预估角度并根据步骤2.1得到的参考频点f0，计算聚焦矩阵t(fj)：

22、t(fj)＝v(fj)uh(fj)

23、其中，u(fj)、v(fj)分别是的左、右奇异矢量，(·)h表示共轭转置运算；

24、步骤2.3、根据步骤2.2得到的聚焦矩阵t(fj)，计算聚焦后参考频点f0处的阵列接收数据矩阵：

25、[r(f0,1),r(f0,2),…,r(f0,j)]＝a(f0,θ)[s(f1),s(f2),…,s(fj)]+[n(f0,1),n(f0,2),…,n(f0,j)]

26、其中r(f0,j)＝t(fj)r(fj)、n(f0,j)＝t(fj)n(fj)为聚焦后的阵列接收数据矩阵、噪声矩阵，a(f0,θ)＝t(fj)a(fj,θ)为参考频率f0处的阵列流型矩阵。

27、步骤3具体按照以下步骤实施：

28、步骤3.1、对整个空域-90°～90°进行n点均匀采样，得到采样网格角度信息且满足n＞＞k和n＞＞m；

29、步骤3.2、假设是目标信号波达方向估计中离第k个目标角度θk最近的网格点，且满足δ是网格间隔，则导向矢量a(f0,θk)在点的一阶泰勒级数展开为：

30、

31、其中，(·)′表示求导运算，|·|表示绝对值运算；

32、步骤3.3、根据稀疏贝叶斯理论及步骤3.2得到的导向矢量泰勒级数展开结果，得

33、

34、其中，

35、

36、β＝[β1,β2,…,βn]，是由0和1组成的向量，当时，对应于的元素为1，否则为0，diag(·)表示对角线运算；

37、步骤3.4、令再根据步骤2得到的参考频点阵列接收数据矩阵，可得宽带信号多频带联合估计的离网格稀疏表示数学模型：

38、

39、其中rj＝[r(f0,1),r(f0,2),…,r(f0,j)]表示阵列接收数据矩阵，nj＝[n(f0,1),n(f0,2),…,n(f0,j)]为高斯白噪声矩阵，为稀疏信号矩阵。

40、步骤4具体按照以下步骤实施：

41、步骤4.1、对步骤3建立的宽带信号多频带联合估计的离网格稀疏表示数学模型进行奇异值分解：

42、rj＝ujlvjh

43、其中uj∈cm×m和vj∈cj×j为酉阵，l是奇异值在主对角线方向递减的对角矩阵；

44、步骤4.2、利用步骤4.1奇异值分解结果对步骤3得到的宽带信号多频带联合估计的离网格稀疏表示数学模型两端同时乘以vjdk，得到降维后的稀疏重构模型：

45、

46、其中，dk＝[ik,0]t，ik是k×k的单位矩阵，β在区间服从均匀分布，并且假设服从λ＝diag(α)，α＝[α1,α2,…,αn]t，且α服从伽马先验c和d是伽马先验的超参数。并假设加性噪声nsv服从分布，cn(·|μ,σ)表示服从均值为μ，方差为σ的高斯分布，α0是噪声方差的倒数，满足具有超参数a和b的伽马分布p(α0)＝gamma(a,b)。

47、步骤5具体按照以下步骤实施：

48、步骤5.1、对步骤4得到降维后的稀疏重构模型通过稀疏贝叶斯理论进行求解，得到超参数αn,α0和β迭代公式：

49、

50、

51、

52、其中，(·)-1表示矩阵求逆运算，||·||2表示2范数，||·||f表示矩阵的frobenius范数，表示取实部运算，(·)*表示共轭运算，表示hadamard积运算。pn，pn和pnn分别表示矩阵p的第n行、第n列和第(n,n)项，vn表示向量v的第n项，β-n表示剔除向量β中的第n项之后所形成的向量；

53、步骤5.2、设定参数a,b,c,d，并初始化β＝0，然后根据步骤5.1得到的超参数αn,α0和β的迭代公式迭代更新超参数αn,α0和β；其中var{·}表示向量的方差；

54、步骤5.3、设定容差参数τ和最大迭代次数，做以下判定：

55、若或者未达到最大迭代次数，则输出α0，αn和β，然后根据步骤5.1得到的超参数αn,α0和β的迭代公式继续迭代更新超参数αn,α0和β；

56、若或者到达最大迭代次数，则迭代终止，输出向量αout＝[α1,α2,…,αn]和离格偏移量向量βout＝[β1,β2,…,βn]；

57、步骤5.4、以角度集合为横坐标，以步骤5.3得到的输出向量αout为纵坐标画曲线，可得到目标信号的空间谱。

58、步骤6具体按照以下步骤实施：

59、步骤6.1、利用谱峰搜索函数寻找目标信号空间谱的谱峰，得到目标信号对应的栅格角度信息

60、步骤6.2、根据步骤6.1得到的目标信号对应的栅格角度信息以及步骤5得到的离格偏移向量计算宽带信号多频带联合估计的波达方向结果：

61、

62、本发明的有益效果是，相比于现有的宽带信号波达方向估计方法，得益于三点：1)本发明方法只需建立参考频点的稀疏重构模型，降低了字典矩阵的维数，从而提高算法的重构效率；2)本发明方法引入奇异值分解提取信号子空间，从而降低了接收收据的维数，达到提高算法的计算效率；3)本发明方法建立了多频带联合稀疏贝叶斯模型，实现多频带的联合估计，提高了算法的估计性能。