一种自适应鲁棒卡尔曼滤波的组合导航数据融合方法

本发明属于组合导航数据融合，具体涉及一种自适应鲁棒卡尔曼滤波的组合导航数据融合方法。

背景技术：

1、人工智能的不断发展，给社会带来便捷的同时也为信息化建设提供了有力支撑，导航技术的应用是推动我国无人驾驶、无人机以及移动绘图等领域发展的关键。面对城市复杂环境下的动态定位问题，gnss/ins组合导航是应用最广，复杂度最低的方案之一，目前对于该方案的精度提升是建立在数据融合算法上，其中以卡尔曼滤波算法为主。但是，传统的非线性滤波算法在拒止环境下，并不能获得较好的最优解。

技术实现思路

1、本发明的目的在于针对现有技术的不足，提供一种自适应鲁棒卡尔曼滤波的组合导航数据融合方法，在基于受污正态分布模型scnm的鲁棒卡尔曼滤波算法基础上，加入sage-husa自适应过程，其中sage-husa自适应方案在更新噪声矩阵r的过程中加入自适应因子ε，有助于实时估计噪声的统计特性，减轻滤波器的发散；scnm在增益矩阵kk更新时设置权重系数，用于最小化量测中的异常值，极大的提升了拒止环境下组合导航精度；相较传统算法，本发明方法既限制了系统建模误差对组合过程的影响，又能够削弱量测信息异常对滤波更新过程的干扰，显著提高了组合导航定位精度，非常适合于城市复杂环境下的动态定位。

2、为实现上述目的，本发明采用如下技术方案：

3、一种自适应鲁棒卡尔曼滤波的组合导航数据融合方法，包括以下步骤：

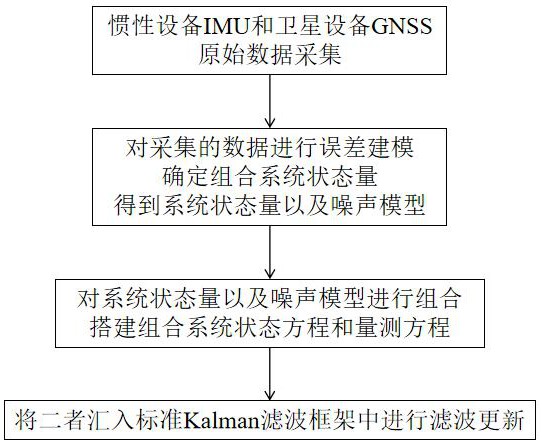
4、步骤s1、惯性设备imu和卫星设备gnss分别按照一定的频率采集原始数据；

5、步骤s2、对采集的imu及gnss数据进行误差建模，确定组合系统状态量xk，得到系统状态量以及噪声模型；

6、步骤s3、对步骤s2中建立的系统状态量以及噪声模型进行组合，搭建组合系统状态方程和量测方程；

7、步骤s4、根据步骤s3中搭建的组合系统状态方程和量测方程，将二者汇入标准kalman滤波框架中进行滤波更新，并在滤波更新过程中加入渐消记忆因子εk和鲁棒估计模型进行修改；

8、步骤s5、重复执行步骤s2～s4，输出xk、pk、εk。

9、具体的，步骤s1中所述惯性设备imu和卫星设备gnss分别按照一定的频率采集原始数据，所述惯性设备imu原始数据包括陀螺仪和加速度计在东北天坐标系三个方向的采样信息，所述卫星设备gnss原始数据包括解算后卫星设备所在的位置和速度信息。

10、具体的，步骤s2中所述对imu及gnss进行误差建模，过程如下：

11、步骤s21、对坐标系进行定义，定义导航坐标系为n系，地心地固坐标系为e系，载体/imu坐标系为b系，组合系统状态量通过惯导误差建立，其中包含三轴下的载体姿态误差，速度误差，位置误差，陀螺仪零偏误差和加速度零偏误差十五个状态量，组合系统状态量xk表示为：

12、

13、上式中，δqn，δvn，δpn分别表示导航坐标系下的姿态、速度和位置误差，和ωb分别表示在imu坐标系下的陀螺仪零偏和加速度计零偏；

14、噪声量wk表示为：

15、

16、上式中，wa和wg表示与之对应的零偏误差，和wε表示imu零偏噪声一阶马尔科夫参数；

17、步骤s22、将imu陀螺仪和加速度计零偏噪声建模为一阶马尔可夫过程，其公式表示为：

18、

19、上式中，ta和tg为时间常数。

20、具体的，步骤s3中所述搭建组合系统状态方程和量测方程，过程如下：

21、步骤s31、将imu陀螺仪和加速度计零偏噪声建模为一阶马尔可夫过程，系统状态方程表示为：

22、xk＝akxk-1+wk-1     (4)

23、上式中，xk和xk-1分别表示k和k-1时刻时的系统状态量，ak表示k时刻时的状态转移矩阵；wk-1表示k-1时刻时的状态噪声序列，状态噪声方差阵为q；在不考虑复杂噪声情况下，各时刻的噪声序列均符合高斯白噪声的特性。

24、步骤s32、系统量测方程通过ins得到的位置和速度信息以及gnss得到的位置和速度信息进行做差获取，系统量测量方程表示为：

25、zk＝hkxk+vk     (5)

26、上式中，zk表示k时刻时的系统观测量，hk表示k时刻时的量测转移矩阵，vk表示k时刻时的量测噪声序列，量测噪声方差阵为r。

27、具体的，步骤s4中所述系统状态方程和量测方程在标准kalman滤波框架中的滤波更新过程如下：

28、步骤s41、在标准kalman滤波框架的更新过程中，新息计算表示为：

29、

30、上式中，表示后验量测，z表示真实量测，表示先验量测；

31、量测噪声方差阵的加权递推估计表示为：

32、

33、上式中，p和h分别表示协方差矩阵和量测控制矩阵；

34、在公式(6)和公式(7)的基础上，引入渐消记忆因子εk，设置其初值ε0＝1，而b∈(0,1)称为渐消因子，当k设置的值较大时，表示渐消因子的取值小，量测噪声的自适应能力就强，不过渐消因子的取值也不能过小，防止噪声估计的结果产生波动，渐消记忆因子εk表达式为：

35、

36、步骤s42、为了提升滤波量测更新时的运算效率，对步骤s41的滤波更新过程采用序贯量测的方式进行更新，将更新后的结果作为kalman滤波的输出；

37、步骤s43、为防止序贯量测更新过程中系统初始状态噪声设置偏大对的影响，引入序贯量测递推式对其每个元素进行大小限制，限制形式表示为：

38、

39、上式中，rmin和rmax分别表示量测噪声序列方差阵的限幅系数；

40、步骤s44、在量测噪声方差阵更新的基础上，假设量测噪声服从vk～β1n(0,r1)+β2n(0,r2)，其中β1、β2、r1和r2均为已知项，β1和β2满足β1+β2＝1，r1和r2满足r2-r1>0；采用加权正态分布的规则，用于逼近具有野值的观测噪声误差分布，结合假设，噪声矩阵wk～n(0,q)，观测数据zk-1是xk-1的分布结构，则xk-1进一步表示为：

41、

42、上式中，

43、由于zk-1时xk的先验条件分布密度p(xk|zk-1)仍符合正态分布，即则和mk的大小能够由下式推算得到：

44、

45、上式中，ak/k-1表示离散时间下的状态转移阵，pk-1表示协方差矩阵，q表示状态噪声方差阵；

46、给定zk-1时，zk的预测条件概率密度形式为p(zk|zk-1)＝∫kp(zk|xk)p(xk|zk-1)dxk，对其进行积分运算得到：

47、

48、上式中，若取e{(zk|zk-1)zk|zk-1)t}＝ek，则有：

49、

50、从而推算得到scnm方案的加权系数λk表达式为：

51、

52、步骤s45、将步骤s44中推算的加权系数λk用于最小化量测中的异常值，以加快信号收敛速度。

53、与现有技术相比，本发明具有以下有益效果：

54、本发明在基于受污正态分布模型scnm的鲁棒卡尔曼滤波算法基础上，加入sage-husa自适应过程，其中sage-husa自适应方案在更新噪声矩阵r的过程中加入自适应因子ε，有助于实时估计噪声的统计特性，减轻滤波器的发散；scnm在增益矩阵kk更新时设置权重系数，用于最小化量测中的异常值，极大的提升了拒止环境下组合导航精度；相较传统算法，本发明方法既限制了系统建模误差对组合过程的影响，又能够削弱量测信息异常对滤波更新过程的干扰，显著提高了组合导航定位精度，非常适合于城市复杂环境下的动态定位。