双反应釜系统事件触发自适应抗饱和液位控制方法与流程

本发明涉及双反应釜控制，特别是指一种双反应釜系统事件触发自适应抗饱和液位控制方法。

背景技术：

1、为了确保安全生产、提高生产效率、降低运行成本，需要对反应釜系统的液位进行自动控制。现有的液位控制主要采用pid控制、滑模控制、模糊控制、神经网络控制等方法，没有充分考虑模型参数未知、输入饱和对系统的不利影响，也无法使液位跟踪误差被限制在指定的范围内，造成控制性能变差；此外，采用固定周期控制策略对控制信号进行更新，并没有考虑系统通信资源有限的情况，会造成一定程度的资源浪费。

2、在实际应用中，对于双反应釜生产过程的液位控制，系统模型参数难以精确获得、执行器控制幅值以及通信资源有限，需要设计不依赖模型参数的抗饱和控制器，同时考虑减少控制器与执行器的通信频率，节约系统资源。此外，为了确保跟踪过程的平稳性与精确性，需要将液位跟踪误差限制在指定范围内，实现精确控制。

技术实现思路

1、本发明提出一种双反应釜系统事件触发自适应抗饱和液位控制方法，确保液位跟踪误差被限制在指定的范围内，同时节约通信资源，以及避免输入饱和的发生。

2、本发明的技术方案是这样实现的：双反应釜系统事件触发自适应抗饱和液位控制方法，包括以下步骤：

3、（1）反应釜的液位变量为，液位设定值为，流量控制输入为，为时间变量，，建立双反应釜液位控制系统模型；

4、（2）利用反应釜的液位障碍函数，对液位跟踪误差进行限制，构造受限的跟踪误差变量；

5、（3）基于跟踪误差变量，设计自适应估计值；基于自适应估计值，设计反应釜控制器（反应釜的事件触发抗饱和控制器的简称）的辅助变量；

6、（4）基于辅助变量，设计反应釜控制器的控制信号；基于控制信号，设计反应釜的流量控制输入，将流量控制输入施加于反应釜的执行器；

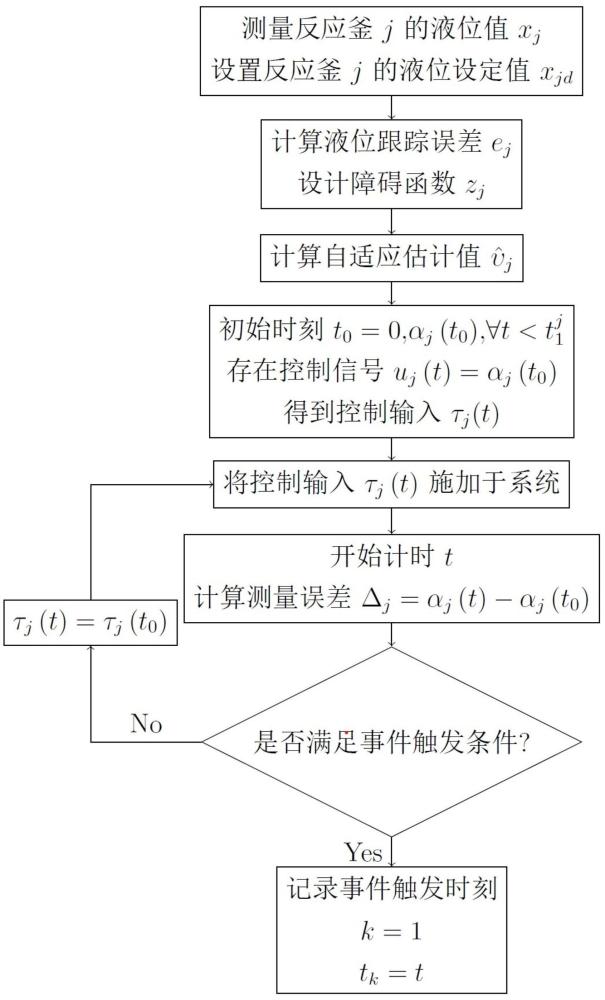
7、（5）定义切换阈值事件触发条件，若不满足触发条件，则控制信号保持不变；若满足触发条件，则更新控制信号。

8、进一步地，步骤（1）中，建立双反应釜液位控制系统模型为

9、(1)

10、其中对应反应釜1，函数，对应反应釜2，函数，为反应釜1出口调节阀的截面积，为反应釜2出口调节阀的截面积；为正常数，为反应釜入口调节阀的截面积，为反应釜釜体的横截面积，为重力加速度，，正常数为流量控制输入额定的最大控制幅值。

11、进一步地，步骤（2）中，构造受限的跟踪误差变量为

12、(2)

13、其中，辅助变量，记作，其中液位障碍函数满足：，存在正常数，正常数，正常数，能够确保，，液位跟踪误差。

14、进一步地，步骤（3）中，设计自适应估计值为

15、(3)

16、其中正常数为设计参数；为关于时间变量的光滑函数，记作，满足：，，且存在常数，使。

17、进一步地，步骤（3）中，设计辅助变量为

18、(4)

19、其中正常数、正常数为设计参数。

20、进一步地，步骤（4）中，设计控制信号为

21、(5)

22、正常数、正常数分别表示反应釜控制器的第个、第个触发时刻，为正整数；式（5）表示控制信号在当前时刻的值为辅助变量在时刻的值；初始时刻，，。

23、进一步地，步骤（4）中，反应釜的流量控制输入为

24、(6)

25、正常数为流量控制输入额定的最大控制幅值。

26、进一步地，步骤（5）中，定义切换阈值事件触发条件为

27、(7)

28、比例阈值设计参数，固定阈值设计参数

29、(8)

30、切换阈值设计参数；测量误差为，表示当前时刻辅助变量与上一触发时刻的差值；

31、若不满足触发条件式(7)，则控制信号一直保持公式(5)；若满足触发条件式(7)，则记录当前满足的时刻为，更新控制信号，。

32、进一步地，还包括步骤（6）闭环稳定性分析：对于双反应釜液位控制系统模型，利于设计的跟踪误差变量、自适应估计值、辅助变量、控制信号和流量控制输入，结合切换阈值事件触发条件，使闭环系统全局渐近稳定，液位跟踪误差，且始终满足。

33、进一步地，闭环稳定性分析的具体方法如下：

34、根据拉格朗日中值定理可知，流量控制输入可以等价为

35、(10)

36、其中，未知常数满足；因此，；

37、定义lyapunov函数

38、(13)

39、由式(2)和式(13)可知，如果在初始时刻的函数值满足，且所设计的反应釜控制器始终满足；

40、定义向量，关于向量的闭环系统为

41、(16)

42、其中，；

43、由式（16）得到：

44、(17)

45、定义开集：

46、(18)

47、其中，初始时刻，；此外，由于液位设定值以及函数在时间变量上是全局lipschitz的；液位障碍函数是有界可导的，函数是全局lipschitz的；定义为时间区间的最大值，上述条件保证了式(17)在时间区间上最大解是存在且唯一的；为了求一个反例，假设；

48、对式(13)中的求导，并结合式(2)和式(16)可得

49、(22)

50、其中时变增益为

51、(21)

52、假定辅助变量满足以下性质：

53、(26)

54、结合切换阈值事件触发条件式（7）可知，

55、(36)

56、其中为绝对值的最大值；

57、由式（36）结合，可知，

58、(38)

59、其中，为未知正常数；

60、结合式（38）和式（26）以及可知，

61、(41)

62、其中未知正常数、未知常数为

63、(40)

64、定义变量为未知常数的自适应估计值，估计误差为，结合式(3)，对未知常数进行逼近；

65、定义lyapunov函数为

66、(42)

67、其中正常数为设计参数，对式(42)求导，并结合式(41)、式（3）和式（4）可得

68、(45)

69、对式(45)不等号两侧在上积分可知

70、(46)

71、由于为关于时间变量的光滑函数，结合式(46)可得

72、(48)

73、结合式(42)可知，

74、(49)

75、式(49)等价为，

76、(50)

77、注意到、、、均为大于零常数，因此；

78、因此，存在一个紧凑的子集

79、

80、使式(17)解的最大值满足，；因此，，即对于所有的都是有定义的；由于，，结合式(50)可以证明；更进一步，由式(50)已证明；此外，利用式(48)可知

81、(51)

82、另一方面，将上述有界的结果结合式(16)可得，；利用barbalat引理，推导出，即，即实现了渐近跟踪，证明完毕。

83、本发明的有益效果：

84、本发明利用障碍函数对液位跟踪误差进行限制，设计基于双曲正切函数的自适应控制方法，并结合事件触发机制对所设计的控制信号进行采样，最终计算出流量控制输入；该控制方法能够始终确保液位跟踪误差被限制在指定的范围内，同时避免了输入饱和的发生，能够在满足所设计定的事件触发条件时对控制信号进行更新并传输至执行器，节约通信资源，较少执行器的操纵频率，延长使用寿命。本发明所提出的方法更符合实际工程应用，满足不同场景的需求，具有良好的控制性能，应用范围更广。