四旋翼无人机固定时间自适应非奇异轨迹跟踪控制方法

本发明属于无人机自主飞行控制，具体涉及一种四旋翼无人机固定时间自适应非奇异轨迹跟踪控制方法。

背景技术：

1、与固定翼无人机(uav)相比，旋翼类无人机拥有垂直降落和空中停留等优势，其结构简洁、承载能力强大，因此在军事、民用以及科研领域得到了广泛的运用，并且引起了国内外学者的高度关注和深入研究。位姿控制系统设计是无人机能够实现自主飞行的关键技术。虽然四旋翼无人机拥有6个自由度，但仅有4个独立的控制输入，是一个典型的欠驱动系统。此外，四旋翼无人机的动力学还表现出多输入多输出、高度耦合以及高度非线性等特性。这都大大增加了四旋翼无人机控制系统的设计难度。

2、目前，许多先进的控制方法在无人机位姿控制领域取得应用[1-3]。pounds[4]等以x-4无人机为原型，设计了pid控制器来调节无人机的位姿。das等[5]基于拉格朗日形式的动力学模型，采用反步法进行四旋翼无人机控制器设计。lee等[6]提出反馈线性化方法和滑模控制方法并进行比较，滑模控制方法在噪声条件下能偶取得更好的性能。raffo等[7]基于模型预测控制方法设计位置控制器，并基于非线性h∞控制方法设计姿态控制器。文献[8]开发了一种基于滑模干扰观测器的滑模控制方法，对模型不确定和外界扰动具有较强的鲁棒性。文献[9]将四旋翼飞行器的动力学模型分为全驱动子系统和欠驱动子系统，并基于二阶滑模控制方法进行控制器设计。文献[10]提出一种容错控制方法，采用间接神经网络逼近方法对执行机构故障进行补偿，控制器结构简单，易于机载实现。文献[11]采用一种自适应模糊跟踪控制方法，使用模糊逻辑系统来逼近无人机系统的未建模动态信息。

3、收敛时间是无人机位姿控制的一项重要性能指标。例如，当采用多无人机协同追踪机动目标时，整个追踪任务期望能在给定的时间内完成。然而，上述控制器大都是渐近稳定或指数稳定的，并没有将收敛时间考虑到问题研究中，在实际应用中缺乏对收敛时间长短的掌握。相较之下，有限时间控制方法能够保证系统状态在有限时间内收敛至平衡位置[12-13]。文献[14]针对四旋翼无人机提出了一种基于干扰观测器的非奇异快速终端滑模控制方法，在模型不确定、外部干扰和执行机构饱和情况下仍能实现控制误差快速收敛。文献[15]设计了一种有限时间容错终端滑模控制器，提高了系统对执行机构故障的响应速度。文献[16]提出了一种有限时间自适应滤波反步滑模控制方法，用于四旋翼无人机的位姿控制。需要指出的是，有限时间控制方法的收敛时间上界严重依赖于系统的初始状态。为了克服该不足，在有限时间控制方法的基础上，固定时间控制方法进一步被提出。固定时间控制方法能够保证系统状态在固定时间内收敛至平衡位置且收敛时间上界与系统的初始状态无关[17-18]。文献[19]提出了一种基于微分平坦的固定时间反步滑模控制策略，避免了传统反步法存在的“计算爆炸”问题。文献[20]提出基于固定时间干扰观测器的鲁棒容错跟踪控制方法，能够消除复合干扰对飞行品质的影响。因此，固定时间控制更有实际意义，但在进行自主飞行跟踪时候使用滑膜控制通常会出现抖振现象。

4、综上，研究一种重视收敛时间，且能够最大程度避免抖振现象的轨迹跟踪控制方法是非常有必要的。

5、上述中引用文献如下：

6、[1]kendoul f.survey of advances in guidance,navigation,and control ofunmanned rotorcraft systems.journal of fieldrobotics,2012,29(2):315-378.

7、[2]ns,m,efe feedback control strategies for quadrotor-typeaerial robots:a survey.transactions ofthe institute of measurement andcontrol,2016,38(5):529-554.

8、[3]lee h,kim hj.trajectory tracking control of multirotors frommodelling to experiments:a survey.internationaljournal of control,automationand systems,2017,15(1):281-292.

9、[4]pounds p,mahony r,corke p.modelling and control of a largequadrotor robot.control engineering practice,2010,18(7):691-699.

10、[5]das a,lewis f,subbarao k.backstepping approach for controlling aquadrotor using lagrange form dynamics.journal of intelligent and roboticsystems,2009,56(1-2):127-151.

11、[6]lee d,kim hj,sastry s.feedback linearization vs.adaptive slidingmode control for a quadrotor helicopter.international journal of control,automation and systems,2009,7(3):419-428.

12、[7]raffo gv,ortega mg,rubio fr.an integral predictive/nonlinear h∞control structure for a quadrotor helicopter.automatica,2010,46(1):29-39.

13、[8]besnard l,shtessel yb,landrum b.quadrotor vehicle control viasliding mode controller driven by sliding modedisturbance observer.journal ofthe franklin institute,2012,349(2):658-684.

14、[9]zheng e-h,xiong j-j,luo j-l.second order sliding mode control fora quadrotor uav.isa transactions,2014,53(4):1350-1356.

15、[10]song y,he l,zhang d,qian j,fu j.neuroadaptive fault-tolerantcontrol of quadrotor uavs:a more affordablesolution.ieee transactions onneural networks and learning systems,2019,30(7):1975-1983.

16、[11]li c,wang y,yang x.adaptive fuzzy control of a quadrotor usingdisturbance observer.aerospace science andtechnology,2022,128:107784.

17、[12]bhat sp,bernstein ds.finite-time stability of continuousautonomous systems.siam journal on control andoptimization,2000,38(3):751-766.

18、[13]bhat sp,bernstein ds.geometric homogeneity with applications tofinite-time stability.mathematics of control,signals,and systems,2005,17(2):101-127.

19、[14]马亚丽,宗群,董琦,尤明.执行器饱和情况下四旋翼无人机的快速终端滑模控制.信息与控制,2017,46(2):204-210+217.

20、(ma yali,zong qun,dong q,you ming.fast terminal sliding mode controlfor quadrotor unmanned aerialvehicle with actuator saturation.information andcontrol,2017,46(2):204-210+217.)

21、[15]张思洁,吴怀宇,郑秀娟.具有执行器故障的四旋翼无人机有限时间容错控制.控制理论与应用,2023,40(7):1270-1276.(zhang sj,wu hy,zheng xj.finite-timefault tolerant control of quadrotor uav with actuator faultscontrol theoryand applications,2023,40(7):1270-1276.)

22、[16]wang j,alattas ka,bouteraa y,mofid o,mobayen s.adaptive finite-time backstepping control tracker forquadrotor uav with model uncertainty andexternal disturbance.aerospace science and technology,2023,133:108088.

23、[17]polyakov a.nonlinear feedback design for fixed-time stabilizationof linear control systems.ieee transactions onautomatic control,2012,57(8):2106-2110.

24、[18]jiang b,hu q,friswell mi.fixed-time attitude control for rigidspacecraft with actuator saturation and faults.ieee transactions on controlsystems technology,2016,51(5):332-340.

25、[19]ai x,yu j.fixed-time trajectory tracking for a quadrotor withexternal disturbances:a flatness-based sliding modecontrol approach.aerospacescience and technology,2019,89:58-76.

26、[20]liu k,wang r,zheng s,dong s,sun g.fixed-time disturbanceobserver-based robust fault-tolerant trackingcontrol for uncertain quadrotoruav subject to input delay.nonlinear dynamics,2022,107(3):2363-2390.

技术实现思路

1、本发明的目的在于，提供一种四旋翼无人机固定时间自适应非奇异轨迹跟踪控制方法，以解决现有技术未将收敛时间作为性能指标，并且在飞行过程中出现抖振现象从而影响飞行质量的技术问题。

2、为了达到上述目的，本发明采用如下技术方案予以解决：

3、一方面，本发明提供了一种四旋翼无人机固定时间自适应非奇异轨迹跟踪控制方法，包括位置环控制策略a和姿态环控制策略b；其中：所述的位置环控制策略a如下：

4、a1：固定时间自适应非奇异终端滑模控制律设置为：

5、

6、式中，m0为无人机原始质量；k11>0，k12>0；g为重力加速度；e3＝[0,0,1]t为竖直方向的单位矢量；为期望位置的加速度；控制参数h11>0，h12>0，0<α<1，β>1；

7、λ11＝diag{|xe|α-1,|ye|α-1,|ze|α-1}，λ12＝diag{|xe|β-1,|ye|β-1,|ze|β-1}，xe、ye、ze分别为x方向、y方向、z方向的位置跟踪误差；η1>0；为的估计，bu>0；

8、sigα(z)＝[|z1|αsgn(z1),…,|zn|αsgn(zn)]

9、sigβ(z)＝[|z1|βsgn(z1),…,|zn|βsgn(zn)]

10、其中，z为矢量，有n个变量到z1～zn；

11、

12、其中，s1为固定时间终端滑模面；为速度跟踪误差；跟踪误差pe＝p-pd，p为无人机实际位置，pd为期望跟踪的参考位置；

13、satσ(λ11)＝[satσ(λ11,1),satσ(λ11,2),satσ(λ11,3)]为饱和函数：

14、

15、式中，σ>0；

16、a2：参数自适应律设置为：

17、

18、式中，控制参数为γ11>0，γ12>0；

19、所述的姿态环控制策略b如下：

20、b1：固定时间自适应非奇异终端滑模控制律设置为：

21、

22、式中，j0为初始转动惯量；控制参数k21>0，k22>0；为参考姿态的加速度；c0为科氏力与离心力项初始值；为角加速度；η2>0，为的估计；bτ>0；

23、λ21＝diag{|φe|α-1,|θe|α-1,|ψe|α-1}λ22＝diag{|φe|β-1,|θe|β-1,|ψe|β-1}

24、s2＝θe+h21sigα(θe)+h22sigβ(θe)

25、式中，φe、θe、ψe分别代表无人机的横滚角、俯仰角、偏航角的跟踪误差；s2为固定时间终端滑模面；控制参数h21>0，h22>0；跟踪角速度误差θe＝θ-θd，θd为期望跟踪的参考姿态；

26、b2：参数自适应律设置为：

27、

28、式中，控制参数为γ21>0，γ22>0。

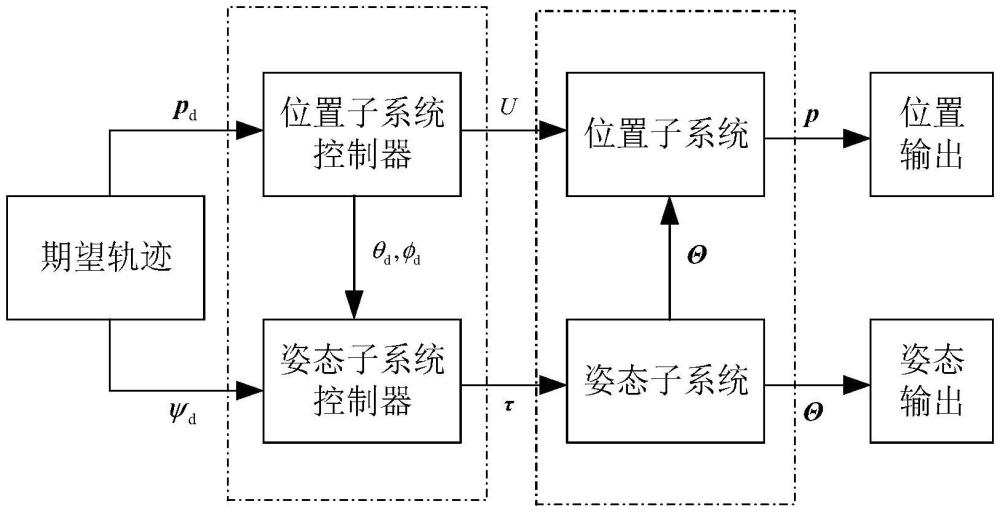
29、另一方面，本发明还提供了一种四旋翼无人机固定时间自适应非奇异轨迹跟踪控制器，采用双环控制结构，具体包括位置环控制器和姿态环控制器，其中，位置环控制器采用位置环控制策略，姿态环控制器采用姿态环控制策略。

30、相较于现有技术，本发明具有如下技术效果：

31、首先，设计了位置环和姿态环的双环控制策略，位置环和姿态环控制器均采用固定时间自适应非奇异终端滑模控制，通过双环控制分别对位置、姿态子系统进行控制。稳定性分析表明，整个闭环系统是实际固定时间稳定的，能够使位置和姿态跟踪误差在固定时间内收敛至零的邻域内，实现了位置和姿态跟踪响应快的效果，达到了无人机快速逼近期望轨迹的目的。

32、其次，设计了新型参数自适应律，与非奇异终端滑模控制相结合，对集总不确定项范数上界的平方进行估计，使整个控制器是光滑的，实现了在不损失控制精度的同时极大地避免了抖振现象。

33、本发明进行了仿真实验，通过与经典比例微分控制方法进行对比，验证了本发明的控制方法的有效性和优越性。