一种基于势博弈的多飞行器分布式任务规划方法

本发明涉及一种基于势博弈的分布式任务规划方法，用于解决多飞行器在复杂环境条件下多飞行器任务规划问题，属于多飞行器任务规划领域。

背景技术：

0、技术背景

1、多飞行器系统越来越多地被用来执行各种复杂任务，包括情报侦察与战场监视任务、自然灾害救援任务、搜索与营救任务、森林灭火、农业灌溉、天气预报等，为了使其适应更复杂多变的任务环境，需要提高多飞行系统的自主规划能力。

2、在任务的实际执行过程中，由于受到飞行器自身、任务需求和飞行环境等因素的制约，多飞行器的自主规划与智能决策是一个十分复杂的问题，主要体现为：飞行器飞行环境日益复杂化，飞行器由于其自身的优势及广阔的发展前景，已越来越受到各国军队的重视，所以，其飞行环境已经变得越来越复杂，除了常规的威胁、障碍，还需要考虑飞行环境的动态性和不确定性，且无人飞行器由于其自身的性能约束，往往不能获取准确实时的全局态势信息，且无法及时响应态势的变化；飞行器的异构性，在任务决策与规划过程中，执行特定的任务往往需要飞行器具备特定的功能，因此需要考虑飞行器自身的性能差异与功能差异；任务自身的复杂性，在任务规划过程中需要考虑任务收益值的时变性、任务之间的耦合性、任务的不确定性等因素；分布式通信的局限性，由于多飞行器的分布性，在任务规划的过程中其数据交互往往是依托于分布式通信链路的，而通信链路需要考虑其自身的通信带宽、通信频率等限制，因此，规划过程中各无人飞行器获取到的信息可能是非同步、非一致的，这就对多无人飞行器的任务规划问题带来了极大的困难。

3、通过对上述对任务规划特点分析可知，为了保证各飞行器之间有效地进行协同和协作以确保高效率、高成功率执行任务，需要通过高自主的任务分配和规划策略实现，这对多飞行器系统的自主任务规划系统提出了极大的需求。利用博弈论的思想，将每个飞行器视作智慧的个体参与到任务规划中，可以大大提高多飞行器系统进行分布式任务规划的自主性。

4、本发明则针对上述需求研究基于势博弈的多飞行器任务规划方法，对进一步提高多飞行器的自主任务规划能力具有重要的理论意义和工程价值。

技术实现思路

1、发明目的

2、为了解决上述技术问题，本发明的目的在于提供一种基于势博弈的多飞行器分布式任务规划方法以应对任务规划环境中的多种约束条件，保证多飞行器系统在受到飞行器自身、任务需求和飞行环境等因素制约的情况下仍能高效率、高准确率的协同执行任务。

3、技术方案

4、为了实现上述目的，本发明采用以下技术方案：

5、本发明为一种基于势博弈的多飞行器分布式任务规划方法，所述方法具体包括以下步骤：

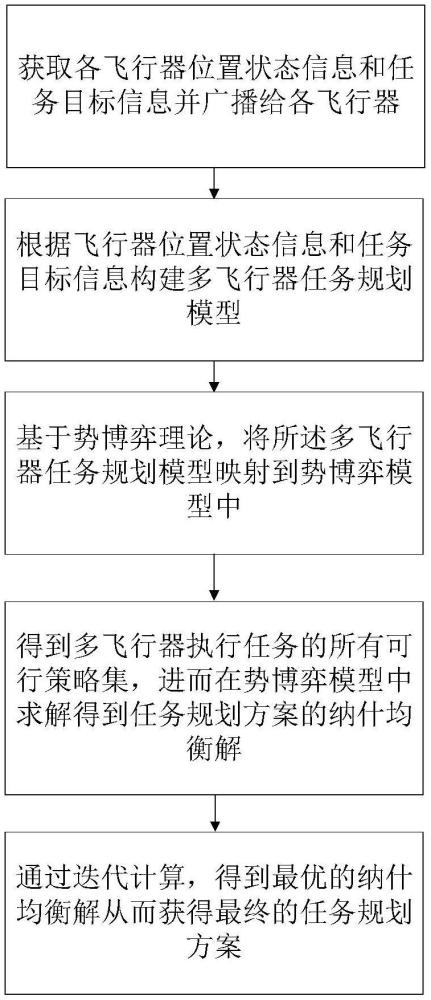
6、步骤一，获取各飞行器位置状态信息和任务目标信息并广播给各飞行器；

7、步骤二，根据飞行器位置状态信息和任务目标信息构建多飞行器任务规划模型；

8、步骤三，将所述多飞行器任务规划模型映射到势博弈模型中；

9、步骤四，基于所述势博弈模型计算多飞行器执行任务的所有可行策略集，在势博弈模型中求解得到任务规划方案的纳什均衡解；

10、步骤五，迭代计算，得到最优的纳什均衡解从而获得最终的任务规划方案。

11、进一步的，以多航天器为例，所述步骤一具体包括以下过程：

12、步骤1.1，获取由n个航天器组成的多航天器系统中各航天器初始位置、燃料负载、和机载设备信息，以及m个任务目标对应的位置信息、功能要求和时间窗口信息；

13、步骤1.2，将步骤1.1中涉及的各信息及要求广播给每个航天器。

14、进一步的，所述步骤二具体包括以下过程：

15、步骤2.1，对步骤一中获得的数据信息进行数学描述，用四元组<t,a,c,r>来表示任务规划问题，其中t＝{t1,…,tj,…,tm}为任务集，tj表示第j个任务；a＝{a1,…,ai,…,an}为航天器集合，ai表示第i个航天器；c为约束集，表示多航天器系统分布式任务规划过程中需要满足的各项约束条件；r表示多航天器系统执行任务所对应的任务总收益；

16、得到任务规划的模型如下：

17、

18、其中，χ是决策变量矩阵，χ＝[χij]n×m，χij∈{0,1}，χi,j＝1表示第i个航天器选择执行第j个任务，反之航天器i不执行任务j；rij表示航天器i执行任务j的收益，为得到rij的数值，定义函数rij＝δijrj0,δij∈[0,1]，rj0表示任务j的初始收益，δij表示航天器i执行任务j的能力系数，cij是影响航天器i执行任务j的任务收益的约束集合；

19、步骤2.2，对步骤2.1中所述约束进行数学建模，包括任务执行的功能约束、时间约束和燃料消耗约束；

20、任务执行的功能约束：采用f＝[fij]n×m来表示航天器i是否具备执行任务j的功能，其中fij∈{0,1}用于标识航天器i是否具备执行任务j的能力；

21、任务执行的时间约束：任务j需要在具体的时间窗口内完成，表示为其中，表示任务窗口的开启时间，表示任务窗口的结束时间；任务j的开始执行时间由所有参与执行任务j的航天器中最晚的到达时间决定，即：

22、

23、定义此时最晚到达的执行任务j的航天器为：

24、

25、任务执行的燃料消耗约束：轨道高度r越大，对应的速度v越小。将航天器i在执行任务j过程中产生的能耗在数值上定义为：

26、

27、其中，dij为航天器i与任务j目标位置的轨道高度差，ri为航天器i距离地球的轨道高度，为航天器i在执行任务j过程的姿态调整角度，κ,λ,γ分别对应轨道高度差系数、轨道高度系数和姿态调整角度系数；

28、设定单个航天器执行任务消耗的能源累积不超过其能源载荷：

29、

30、其中，qri(i)为航天器i的初始能源；qmi(i)为航天器安全运行的能源阈值；

31、步骤2.3，根据步骤2.2得到的约束条件信息，将任务j被执行的收益定义为：

32、

33、其中，k∈[0,1]，e为自然常数，η为时间折扣系数，ρ为燃料消耗折扣系数。

34、进一步的，所述步骤三具体包括以下过程：

35、步骤3.1，将步骤二所述多飞行器任务规划模型映射为如下有限策略集博弈模型：

36、g＝(a,s,{ui})  (7)

37、其中，s＝s1×…×si×…×sn表示多航天器系统的策略空间，si表示航天器i可以执行的所有策略集，设定航天器i自身的策略为si，si∈si，其他航天器的策略集为s-i，s-i＝(s1,…si-1,si+1,…,sn)，则多航天器系统的策略集可表示为s＝(si,s-i)；ui表示航天器i的策略收益函数；

38、步骤3.2，定义所述博弈模型中当前局势为多航天器系统的策略集s＝(si,s-i)，对应局势收益函数表示为：

39、u(si,s-i)＝∑j∈srj  (8)

40、其中，ui(si,s-i)表示在对应局势中，航天器i执行任务的策略收益，ui(si,s-i)的值与si和s-i有关，表示为：

41、

42、其中，u(0,s-i)表示除航天器i以外的航天器执行策略对应的局势收益；在当前局势下进行策略更新时所对应的策略收益函数如下：

43、

44、其中，s′i是航天器i策略更新后执行的策略；

45、步骤3.3，定义在所述有限策略集博弈模型g＝(a,s,{ui})中，若存在函数φ:s→r，对所有s,s'∈si，满足：

46、ui(s′i,s-i)-ui(si,s-i)＝φ(s′i,s-i)-φ(si,s-i)  (11)

47、则g为势博弈，φ为相应势函数；将φ定义为φ＝∑j∈srj，即局势收益；对于满足：

48、

49、表示为：

50、

51、此时对应的策略集为纳什均衡。

52、进一步的，所述步骤四具体包括以下过程：

53、步骤4.1，设计算法得到多飞行系系统执行任务的所有可行策略集，包括如下步骤：

54、(1)飞行器和任务数据进行参数初始化；

55、(2)飞行器选取可行策略集合，设置任务包1、2、3、……，其中任务包1中记录可执行任务数量为1的策略，任务包2在获得任务包1的基础上记录可执行任务数量为2的策略，任务包3在获得任务包2的基础上记录可执行任务数量为3的策略，直到得到该飞行器的所有可行策略集；

56、(3)转到下一个飞行器得到对应的可行策略集，直到得到所有飞行器的可行策略集；

57、步骤4.2，基于所有飞行器可行策略集，通过基于势博弈的多飞行器任务规划算法得到任务规划方案，包括如下步骤：

58、(1)设置迭代次数和初始局势并初始化全局收益和任务规划方案；

59、(2)随机选取飞行器选择使当前局势最大的策略，同时对任务规划方案进行更新，记录任务所需时间，燃料消耗值和全局收益值；

60、(3)重复执行上一步骤，直到全局收益无法增加，达到纳什均衡解，进行下一轮迭代计算；

61、(4)在得到的纳什均衡解中选取其中的最大值，得到最终的任务规划方案。

62、本发明的有益效果为：

63、(1)本发明考虑了多飞行器系统在受到飞行器自身、任务需求和飞行环境等因素制约情况下的任务规划问题，所设计的任务规划方法确保了各飞行器的自主性和执行任务的高成功率。

64、(2)设计引入势博弈理论，将多飞行器分布式任务规划模型映射到博弈模型中。

65、(3)所设计的可行策略集计算算法和基于势博弈的多飞行器分布式任务规划算法确保了在考虑多种约束条件的情况下各飞行器都能得到最优的任务执行策略，从而得到最优的任务规划方案。

66、(4)在多飞行器分布式任务规划上具有很好的实际意义和应用前景。

67、附图表说明

68、图1为基于势博弈的多飞行器分布式任务规划方法流程示意图；

69、图2为本发明实施例中多飞行器分布式任务规划模型架构示意图；

70、图3为本发明实施例中霍曼转移轨道示意图；

71、图4为本发明实施例中基于势博弈的分布式任务规划算法的流程示意图；

72、图5为本发明实施例中各飞行器的飞行轨迹示意图。