基于ESMD-SDEO的行波波头时间标定方法

本发明涉及行波测距，具体涉及一种基于esmd-sdeo的行波波头时间标定方法。

背景技术：

1、随着对电力系统运行可靠性要求的不断提升，高精度的故障定位技术成为了电力系统运行可靠性的重要保障，而有关输电线路故障定位技术的研究毫无疑问具有重大时代意义。行波测距方法是目前输电线路故障定位的主流方法，在该方法的运行过程中，对于行波波头时间的标定将直接影响到测距的精度，由于行波信号其本身十分复杂，且波头部分没有直观明显的特征，所以如何对行波波头的时间进行准确的标定就成为了亟需解决的难题。

2、对于行波波头时间的标定，一种方法是使用小波变换法来放大行波信号的局部特征从而找到波头所在的部分，如文献[1]:周鲁天,梁睿,彭楠,等.基于arima的矿山电网故障暂态行波波头辨识及故障测距[j].电力自动化设备,2020,40(06):177-188.中记载的。但是小波变换法的准确性在很大程度上受所选择的小波基的影响，对不同信号的适应性较低，且计算过程复杂计算量大，该方法的时效性难以得到保证。

3、另一种方法是使用经验模态分解法将分解出行波信号的本征模态以及瞬时频率，并将其作为对行波波头进行识别的特征分量，如文献[2]:束洪春,程春和,赵文渊,等.形态学与hht检测相结合的行波波头准确标定方法[j].电力自动化设备,2009,29(07):1-7+37.中记载的。但是这种方法在实际应用中会出现模态混淆的问题，所分解出的一个模态中可能混杂了几个模态的特征从而导致波头识别效果不理想。

4、基于上述分析，使用信号分解算法来分解行波信号进行特征研究分析，从而标定波头时间，可以使用性能更为优越的信号分解算法来达到更高精确度的波头时间标定。

技术实现思路

1、为解决上述技术问题，本发明提供一种基于esmd-sdeo的行波波头时间标定方法，有效解决了在电力系统行波故障测距中对于行波波头到达时间标定不够准确从而导致测距误差的问题。

2、本发明采取的技术方案为：

3、基于esmd-sdeo的行波波头时间标定方法，包括以下步骤：

4、步骤一：对采集到的故障前后1/4工频周期电流行波进行相模变换，得到故障电流行波线模分量；

5、步骤二：使用极点对称模态分解算法esmd将故障电流行波线模分量进行分解，得到多个模态分量和余量；

6、步骤三：使用对称差分能量算子sdeo跟踪行波信号的能量，达到放大行波信号中波头特征的效果；

7、步骤四：找到步骤三中得到的行波信号能量的第一个突变点，该第一个突变点所对应的时间即标记为波头到达时间点。

8、所述步骤一中，对采集到的故障前后1/4工频周期电流行波进行相模变换，得到故障电流行波线模分量；具体如下：

9、对采集到的故障前后1/4工频周期电流行波进行基于karenbauer变换的相模变换，具体公式如下：

10、

11、式中：ia、ib、ic分别为a,b,c三相电流，i0为零模行波分量，i1为线模行波分量。考虑到在实际的工程应用中，行波采集装置所采集到的行波信号会由于环境因素的干扰而产生大量噪声，且不同的故障源之间还存在着不同程度的耦合，使得采集到的行波信号所呈现出的特征非常复杂，不利分析，故引入极点对称模态分解算法(extreme-point symmetricmode decomposition,esmd)即esmd信号分解算法对其进行分解以准确识别其蕴含的故障特征。

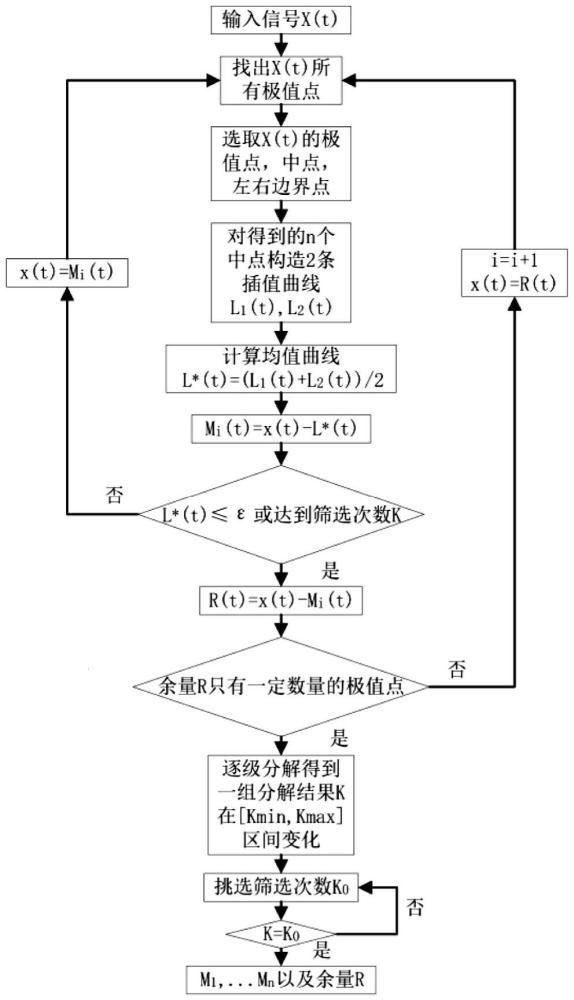
12、所述步骤二包括如下步骤：

13、2.1:筛选出故障电流行波线模分量信号x(t)所有的极大值点以及极小值点，标记为ei，i＝1,2,…,n；n表示的是所选出的极大值以及极小值点的个数；

14、2.2:计算出相邻的两个极值点之间的线段中点，标记为fi，i＝1,2,…,n-1；

15、2.3:使用改进的线性插值方法，分别在信号的左右边界处补充中点，将其分别记为f0以及fn，具体如下：

16、

17、在补充f0时，上式中x,y即对应所补充中点的坐标f0(x,y),x0＝0,y0＝0,x1,y1对应信号初始数据点的坐标(x1,y1)；

18、

19、在补充f1时，上式中xn,yn即对应所补充中点的坐标fn(xn,yn),x0＝0,y0＝0,xn-1,yn-1对应信号末尾数据点的坐标(xn-1,yn-1)；

20、2.4:以步骤2.2中所计算出的n个中点为基础，分别构造出插值线l1与l2，求出它们的均值曲线l*，计算过程如式(1)所示：

21、l*＝(l1+l2)/2(1)；

22、2.5:将x(t)-l*重复进行以上步骤2.1.至步骤2.4，直到将所得出的均值曲线l*控制在误差允许的范围内时，即如式(2)所示：

23、l*|<ε(2)；

24、式中：ε即为误差，当筛选次数已达到最大值k时，此时即:得出所分解到的第一层模态分量m1；

25、2.6:把x(t)-m1作为一个新的原始信号，重复进行以上步骤2.1至步骤2.5，从而依次获得经验模态m2,m3……，该过程将一直持续到剩余的余量r只含有唯一的一个极值点；

26、2.7:将k在其区间[kmin,kmax]内进行变化的取值之后，重复进行以上步骤2.1至步骤2.6，即能够得到多组分解结果，将这几组分解结果计算出其方差比率σ/σ0，之后绘制出σ/σ0关于k的关系趋势图。在所绘制出的关系趋势图中即能够得到当方差比率为最小时，其所对应的筛选次数即为最大筛选次数k0。关于k的关系趋势图代表方差比率σ/σ0以及k之间的相关性。

27、2.8:将筛选次数设定为k0，重复进行以上步骤2.1至步骤2.6，此时所得到的分解结果即为原始信号的最优分解。

28、原始信号x(t)的分解结果表示为：

29、

30、式中，s即为行波信号经过esmd算法分解所得到的模态数；

31、按照以上步骤，即可将故障点产生的行波信号分解为多个不同频段的模态mi(t)以及分解所产生的余量r(t)。

32、在现实情况中，故障电流行波经esmd分解得到的第一层模态函数将会因为噪声的存在而导致波头的特征被掩盖，为解决这一问题，使用对称差分能量算子(symmetricdifferential energy operator,sdeo)跟踪行波信号的能量，达到放大信号中波头特征的效果。

33、所述步骤三包括如下步骤：

34、3.1、分割行波信号：

35、将极点对称模态分解算法esmd分解后的第一层行波信号模态分量m1(n)切分成多个小窗口，记为mi(n)，分割过程中为了保证信号的平滑性以及连续性，将采取滑动窗口的分割方式，如式(4)所示：

36、mi(n)＝m(n+i·l)0≤n≤l(4)；

37、式中：n所代表的是信号的时间索引；i为分割之后的窗口索引；l为每个窗口的长度。

38、3.2、进行对称差分计算：

39、针对分割所得的每个小窗口所包含的信号片段，将其中相邻的数据点进行对称差分计算，如式(5)所示：

40、di(n)＝(mi(n)-mi(n-1))2+(mi(n)-mi(n+1))2(5)；

41、式中：di(n)表示对称差分值；mi(n-1)表示上一相邻窗口所对应的模态分量；mi(n+1)表示下一相邻窗口所对应的模态分量。

42、3.3、对单个窗口进行能量获取：

43、对步骤3.2中所得的相邻数据点的对称差分计算结果进行平方运算，即可得到窗口的能量值，如式(6)所示：

44、ei(n)＝di2(n)(6)；

45、式中：ei(n)表示计算所得的窗口能量值。

46、3.4、计算出信号的全局能量叠加：

47、对步骤3.3中计算所得的所有窗口的能量值进行求和计算，其所得到的结果即为整个信号中的能量分布情况，如式(7)所示：

48、

49、式中：e(n)表示计算所得的总信号能量；n表示分割窗口的总个数。

50、所述步骤四中，原始故障行波信号的突变点情况与分解所得到的模态分量m1波形变化情况是完全对应的，故突变点的变化趋势也遵循着sdeo能量值的极值分布情况，突变点的幅值变化特征与sdeo能量值的强度变化特征也存在着完全的对应关系，故找到步骤三中得到的信号能量的第一个突变点，第一个突变点的数据点所对应的时间，即能够标记为波头到达时间点，即行波波头到达行波采集装置的时间。

51、本发明一种基于esmd-sdeo的行波波头时间标定方法，技术效果如下：

52、1)本发明方法分解行波信号所得到的模态函数相比于其他分解方法精度更高，更能体现行波波头的特征。

53、2)本发明方法相比于其他分解方法，对于不同类型的行波信号具有更良好的适应性。

54、3)本发明方法计算量小，计算速度更快。