不对中直齿轮啮合刚度和齿面载荷分布计算方法及系统

本发明属于齿轮测量，具体涉及一种不对中直齿轮啮合刚度和齿面载荷分布计算方法及系统。

背景技术：

1、齿轮具有传动稳定、传动效率高的特点，在履带车辆、船舶等大型装备的传动系统中被广泛应用。然而，由于制造误差和装配误差的影响，齿轮会出现不对中啮合；此外，对于转子支承齿轮系统，在重载条件下支承转子的柔性变形也会导致齿轮出现多自由度不对中。齿轮的不对中会导致啮合刚度降低，并最终影响齿轮的动态特性、传动效率和使用寿命。

2、目前用于评估不对中直齿轮啮合刚度的方法主要包括能量法和有限元法，其中能量法主要根据齿轮副啮合变形产生的能量以及齿轮副动态啮合力来确定齿轮副的时变啮合刚度，为了研究不对中量对齿轮啮合刚度的影响，通常沿齿宽方向进行切片，并将能量法与切片法相结合，通过计算啮合力沿各坐标轴方向的投影来等效计算不对中条件下的啮合刚度。有限元法通过有限元软件建立相应的齿轮模型，并将不对中量在模型中进行设置，通过软件模拟仿真获得不对中齿轮对的啮合刚度。能量法具有计算简单的优点，但当存在不对中量时，能量法的计算精度较低，而有限元法计算精度较高，但计算效率较低。目前用于评估不对中直齿轮齿面载荷分布的方法主要包括有限元法和齿面承载接触分析，普遍存在计算效率较低的问题。因此，提出一种能够准确高效评估不对中直齿轮的啮合刚度和齿面载荷分布的方法具有重要意义。

技术实现思路

1、为了解决现有技术中存在的问题，本发明提供不对中直齿轮啮合刚度和齿面载荷分布计算方法，能够准确计算多自由度不对中条件下直齿轮对的啮合刚度和齿面载荷分布。

2、为了实现上述目的，本发明采用的技术方案是：一种不对中直齿轮啮合刚度和齿面载荷分布计算方法，包括以下步骤：

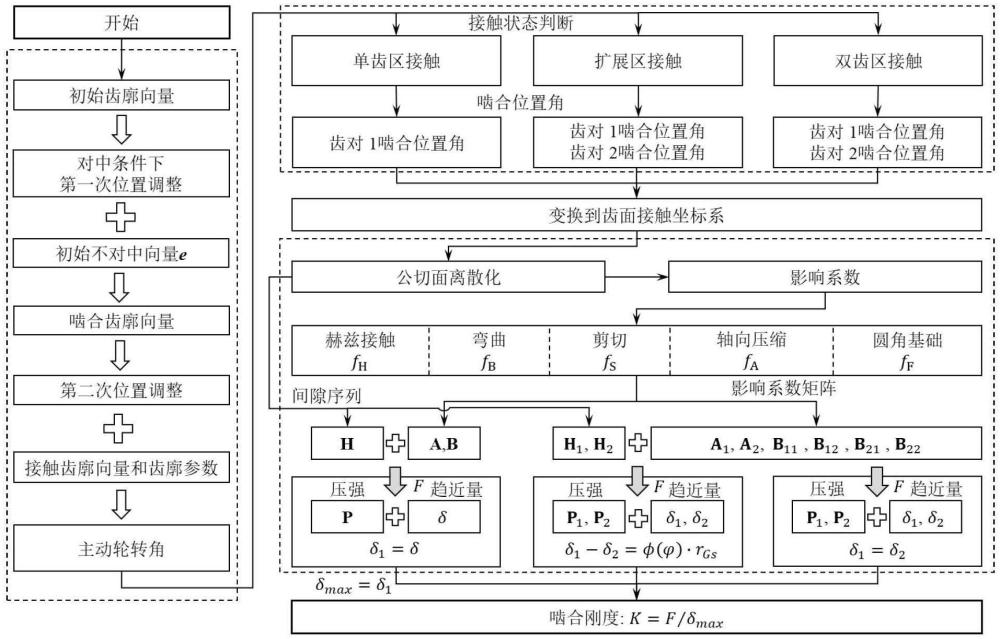
3、基于齿轮几何参数，获得初始齿廓向量，基于齿轮接触控制方程1，并结合齿轮不对中量，将初始齿廓向量转换为啮合坐标系下的啮合齿廓向量，基于齿轮接触控制方程2，将啮合齿廓向量转换为齿廓公切面接触坐标系下的接触齿廓向量，并得到接触齿廓坐标转换矩阵；

4、设定接触齿廓公切面的范围，将公切面在接触坐标系下进行离散化，得到接触坐标系下离散化单元坐标，并基于接触齿廓坐标转换矩阵计算两齿廓沿公切面法向对应的离散化单元之间的间隙h；

5、基于接触坐标系下离散化单元，通过接触齿廓向量和承载接触分析理论计算接触坐标系下离散化单元k在所有n个接触坐标系下离散化单元载荷影响下的弹性变形量wk；

6、基于弹性变形量wk，获得包含离散化单元间的间隙h、两齿面弹性趋近量δ和齿轮啮合力f的齿面承载接触方程组，将齿面承载接触方程组转换为矩阵形式，得到影响系数矩阵a和b，以及由离散化单元间隙值h组成的间隙向量h；

7、结合影响系数矩阵a和b，分别考虑齿轮的单齿啮合区、双齿啮合区和扩展啮合区，得到齿轮的多状态啮合承载接触方程组；

8、基于齿轮的多状态啮合承载接触方程组，通过数值求解得到各离散单元压强，进而乘以离散单元面积得到齿面载荷分布，通过齿轮啮合力f与弹性趋近量δ计算得到齿轮啮合刚度k。

9、进一步的，所述的直齿轮几何参数包括齿轮的模数、齿数、压力角、中心孔半径、齿宽、杨氏模量和泊松比。

10、进一步的，所述的初始齿廓向量包括齿廓位置向量ri(θ,u)和法向量ni(θ)，其中变量θ为齿廓位置角变量，变量u为齿廓位置线变量，所述啮合齿廓向量包括齿廓位置向量rm(θ,u,φ)和法向量nm(θ,φ)，其中，变量φ为齿廓转动角变量，所述接触齿廓向量包括齿廓位置向量rc(θ,u,φ)和法向量nc(θ,φ)，所述的齿轮不对中量包括沿坐标轴的平移不对中量和扭转不对中量，所述的初始齿廓向量表示为：

11、

12、其中，下标g和p分别表示主动齿轮和从动齿轮，rb为齿轮基圆半径，所述齿轮接触控制方程1为：

13、

14、其中，下标g和p分别表示主动齿轮和从动齿轮，表示主动轮齿廓边缘的切向量，表示从动轮齿面的法向量，所述的齿轮接触控制方程2为：

15、

16、其中，表示公切面接触坐标系原点向量，和分别表示接触坐标系三个坐标轴方向的单位向量，表示齿轮侧面的单位法向量。

17、进一步的，所述的接触坐标系以主动轮和从动轮齿廓接触面中点为坐标原点，沿接触面齿宽方向为坐标轴x向，沿接触面法向为坐标轴z向，所述的公切面离散化得到的是面积为s的矩形单元，所述的离散化单元之间的间隙h通过接触坐标系下各离散单元中点对应的两齿廓z向坐标差计算得到。

18、进一步的，所述的弹性变形量其中fkj是单元j对单元k的变形影响系数，ff是弹性基体变形影响系数，pj是单元j的压强，其中变形影响系数fkj是赫兹接触变形影响系数fh,kj、弯曲变形影响系数fb,kj、剪切变形影响系数fs,kj和轴向压缩变形影响系数fa,kj的线性叠加。

19、进一步的，所述的齿面承载接触方程组为：

20、

21、式中，f表示两齿廓间的啮合力，δ表示两齿廓弹性趋近量，将方程组转换为矩阵形式，得到扩展系数矩阵a和b为：

22、

23、以及由离散化单元间隙值h组成的间隙向量h＝[h1 … hn]t。

24、进一步的，所述的多状态啮合承载接触方程组表示为：

25、单齿啮合区承载接触方程组：

26、

27、双齿啮合区承载接触方程组：

28、

29、扩展啮合区承载接触方程组：

30、

31、其中，a1和a2分别表示第一对和第二对啮合齿的影响系数矩阵，b11、b12、b21和b22分别表示以ff11、ff12、ff21和ff22为变量的弹性基体变形系数矩阵，in×1和i1×n分别表示单位列向量和单位行向量，n1和n2分别表示两对啮合齿离散单元的个数，s1和s2分别表示两对啮合齿离散单元的面积，p1和p2分别表示两对啮合齿离散单元的压强向量，h1和h2分别表示两对啮合齿的间隙向量，δ1和δ2分别表示两对啮合齿的弹性趋近量，在双齿啮合区，两对啮合齿趋近量相等，在扩展啮合区，两对啮合齿的弹性趋近量满足如下关系：

32、[δ1(α,f1,f2)-δ2(α,f1,f2)]＝φ(α)rb

33、其中，rb表示主动齿轮基圆半径，f1和f2分别表示两对啮合齿间的载荷，φ(α)表示与转角α相关的齿轮角分离距离。

34、进一步的，所述的数值求解包括：

35、对矩阵进行lu分解，求解每次迭代过程中的压强分布和弹性趋近量，当某一单元的压强求解结果为负时，将该单元压强设为零，进行下一次迭代，直到所有单元的压力值均不小于零为止，最终得到各单元压强和总体趋近量；

36、所述齿面载荷分布通过单元压强乘以单元面积计算得到，所述啮合刚度k＝f/δmax，其中δmax表示参与啮合齿对趋近量的最大值。

37、本发明同时提供一种不对中直齿轮啮合刚度和齿面载荷分布的系统，齿廓向量计算模块、离散模块、弹性变形量计算模块、影响系数矩阵获取模块、接触状态方程建立模块以及解算模块；

38、获得啮合直齿轮的几何参数和载荷条件；

39、齿廓向量计算模块用于基于齿轮几何参数和齿轮不对中量，获得啮合齿轮对的接触齿廓向量和接触齿廓坐标转换矩阵；

40、离散模块用于将公切面在接触坐标系下离散化，得到接触坐标系下离散化单元坐标，并基于接触齿廓坐标转换矩阵计算两齿廓沿公切面法向对应的离散化单元之间的间隙值h；

41、弹性变形量计算模块基于所述接触坐标系下离散化单元，通过接触齿廓向量和承载接触分析理论计算接触坐标系下离散化单元k在所有n个接触坐标系下离散化单元载荷影响下的弹性变形量wk；

42、影响系数矩阵获取模块基于弹性变形量wk，获得包含离散化单元间的间隙h、两齿面弹性趋近量δ和齿轮啮合力f的齿面承载接触方程组，将方程组转换为矩阵形式，得到影响系数矩阵a和b，以及由离散化单元间隙值h组成的间隙向量h；

43、接触状态方程建立模块用于结合影响系数矩阵a和b，分别考虑齿轮的单齿啮合区、双齿啮合区和扩展啮合区，得到齿轮的多状态啮合承载接触方程组；

44、解算模块基于齿轮的多状态啮合承载接触方程组，通过数值求解得到齿面载荷分布，通过齿轮啮合力f与趋近量δ计算得到齿轮啮合刚度k。

45、与现有技术相比，本发明至少具有以下有益效果：本发明提出一种能够准确计算不对中直齿轮啮合刚度和齿面载荷的方法，采用齿轮接触分析理论获得不对中条件下齿轮对的接触位置，将不对中齿轮接触齿面沿公切面进行离散化，计算各离散单元间的弹性变形影响系数，利用载荷变形方程组求解得到接触齿面载荷分布和弹性趋近量，并最终计算得到不对中齿轮对啮合刚度。本发明充分利用了影响系数法计算齿轮弹性变形量的优势，并利用齿轮接触分析理论准确评估了不对中量对齿轮啮合接触的影响，具有计算准确、效率高的优势。使用本方法求解的啮合刚度能够为齿轮传动效率、动态特性和使用寿命研究提供关键基础。