基于时变状态约束和磁滞非线性的直升机控制方法及装置

本发明涉及飞行系统控制，尤其涉及一种基于时变状态约束和磁滞非线性的直升机控制方法及装置。

背景技术：

1、随着航空航天和无人机技术的迅猛发展，以及对小型、灵活和经济高效无人机需求的不断增长，小型无人直升机在军事、商业和民用领域的应用越来越广泛。相比传统的固定翼载人飞机，小型无人直升机具有明显的优势。它们能够垂直起降，并能在狭窄空间内迅速操作，从而增强了操作的灵活性。此外，这些直升机在低空飞行、复杂机动和悬停方面表现出色，使其成为监视、搜索和救援任务的理想选择。

2、然而，小型无人直升机系统具有多输入多输出的非线性特征，包括复杂的动力学建模和耦合效应，使得鲁棒控制的设计变得极为复杂。在实际应用中，直升机控制系统由于机械结构和安全规范的限制，面临时变状态约束问题。如果在设计控制方案时忽略这些约束，可能会显著降低系统的性能，甚至导致系统不稳定。

3、此外，直升机系统还需要应对磁滞现象的重大挑战。过度的磁滞效应不仅会影响系统的稳定性，还可能导致系统遭到严重损害。因此，如何有效地解决这些问题，成为确保直升机系统稳定性和安全性的关键。

技术实现思路

1、本发明实施例的主要目的在于提出一种基于时变状态约束和磁滞非线性的直升机控制方法及装置，能够提升直升机系统在实际应用中的稳定性和安全性。

2、为实现上述目的，本发明实施例的一方面提出了一种基于时变状态约束和磁滞非线性的直升机控制方法，包括以下步骤：

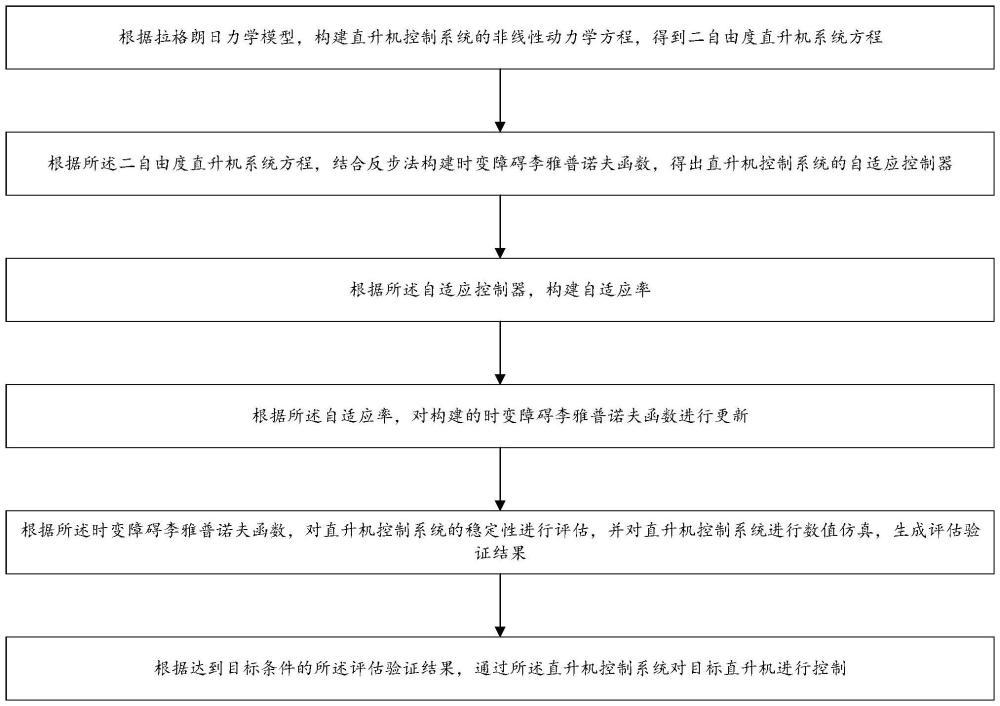
3、根据拉格朗日力学模型，构建直升机控制系统的非线性动力学方程，得到二自由度直升机系统方程；

4、根据所述二自由度直升机系统方程，结合反步法构建时变障碍李雅普诺夫函数，得出直升机控制系统的自适应控制器；

5、根据所述自适应控制器，构建自适应率；

6、根据所述自适应率，对构建的时变障碍李雅普诺夫函数进行更新；

7、根据所述时变障碍李雅普诺夫函数，对直升机控制系统的稳定性进行评估，并对直升机控制系统进行数值仿真，生成评估验证结果；

8、根据达到目标条件的所述评估验证结果，通过所述直升机控制系统对目标直升机进行控制。

9、在一些实施例中，所述根据拉格朗日力学模型，构建直升机控制系统的非线性动力学方程，得到二自由度直升机系统方程的步骤之后，包括以下步骤：

10、根据平滑连续非线性函数向量和直升机控制系统的控制输入信息，对所述二自由度直升机系统方程进行表达式更新，得到基于二自由度直升机系统的非线性动力学方程；

11、选用backlash-like的磁滞非线性模型，得到磁滞非线性模型；

12、根据所述磁滞非线性模型，对所述基于二自由度直升机系统的非线性动力学方程进行更新，并采用径向基函数神经网络来估计直升机控制系统的未知函数，然后配置角度误差、期望轨迹和虚拟控制器。

13、在一些实施例中，所述根据所述二自由度直升机系统方程，结合反步法构建时变障碍李雅普诺夫函数，得出直升机控制系统的自适应控制器这一步骤中，

14、所述时变障碍李雅普诺夫函数的表达式为：

15、

16、其中，v1和v2为设计的时变障碍李雅普诺夫函数，和代表状态约束变量，e1为跟踪误差，e2为误差变量；

17、所述自适应控制器的表达式为：

18、

19、其中，η2为控制增益矩阵，为时变增益参数，用于逼近最优权重，k为磁滞现象斜率具有上界的最大值；ζ为合适的正整数；ξ代表虚拟控制器。

20、在一些实施例中，所述根据所述自适应控制器，构建自适应率这一步骤中，

21、所述自适应率的表达式为：

22、

23、其中，近似于wi*，表示增益矩阵，并且δi>0是小参数。网络权重误差定义为si(z)代表基函数变量。

24、在一些实施例中，所述根据所述时变障碍李雅普诺夫函数，对直升机控制系统的稳定性进行评估，具体为：

25、根据所述时变障碍李雅普诺夫函数、所述自适应率以及杨氏不等式，验证所述时变障碍李雅普诺夫函数的半全局有界性；

26、其中，所述半全局有界性的表达式为：

27、

28、其中，λmin(υi)为最小特征值；η1i和η2i为时变增益参数。

29、在一些实施例中，所述对直升机控制系统进行数值仿真，具体为：

30、通过软件matlab对直升机控制系统进行数值仿真，验证直升机控制的效果并得到分析结果。

31、本发明实施例的另一方面还提供了一种基于时变状态约束和磁滞非线性的直升机控制装置，包括：

32、第一模块，用于根据拉格朗日力学模型，构建直升机控制系统的非线性动力学方程，得到二自由度直升机系统方程；

33、第二模块，用于根据所述二自由度直升机系统方程，结合反步法构建时变障碍李雅普诺夫函数，得出直升机控制系统的自适应控制器；

34、第三模块，用于根据所述自适应控制器，构建自适应率；

35、第四模块，用于根据所述自适应率，对构建的时变障碍李雅普诺夫函数进行更新；

36、第五模块，用于根据所述时变障碍李雅普诺夫函数，对直升机控制系统的稳定性进行评估，并对直升机控制系统进行数值仿真，生成评估验证结果；

37、第六模块，用于根据达到目标条件的所述评估验证结果，通过所述直升机控制系统对目标直升机进行控制。

38、本发明实施例的另一方面还提供了一种电子设备，包括处理器以及存储器；

39、所述存储器用于存储程序；

40、所述处理器执行所述程序实现如前面所述的方法。

41、本发明实施例的另一方面还提供了一种计算机可读存储介质，所述存储介质存储有程序，所述程序被处理器执行实现如前面所述的方法。

42、本发明实施例的另一方面还提供了一种计算机程序产品，包括计算机程序，所述计算机程序被处理器执行时实现如前面所述的方法。

43、本发明实施例至少包括以下有益效果：本发明提供一种基于时变状态约束和磁滞非线性的直升机控制方法及装置,该方案根据拉格朗日力学模型，构建直升机控制系统的非线性动力学方程，得到二自由度直升机系统方程；根据所述二自由度直升机系统方程，结合反步法构建时变障碍李雅普诺夫函数，得出直升机控制系统的自适应控制器；根据所述自适应控制器，构建自适应率；根据所述自适应率，对构建的时变障碍李雅普诺夫函数进行更新；根据所述时变障碍李雅普诺夫函数，对直升机控制系统的稳定性进行评估，并对直升机控制系统进行数值仿真，生成评估验证结果；根据达到目标条件的所述评估验证结果，通过所述直升机控制系统对目标直升机进行控制，本发明能够提升直升机系统在实际应用中的稳定性和安全性。

技术特征：

1.一种基于时变状态约束和磁滞非线性的直升机控制方法，其特征在于，包括以下步骤：

2.根据权利要求1所述的一种基于时变状态约束和磁滞非线性的直升机控制方法，其特征在于，所述根据拉格朗日力学模型，构建直升机控制系统的非线性动力学方程，得到二自由度直升机系统方程的步骤之后，包括以下步骤：

3.根据权利要求1所述的一种基于时变状态约束和磁滞非线性的直升机控制方法，其特征在于，所述根据所述二自由度直升机系统方程，结合反步法构建时变障碍李雅普诺夫函数，得出直升机控制系统的自适应控制器这一步骤中，

4.根据权利要求3所述的一种基于时变状态约束和磁滞非线性的直升机控制方法，其特征在于，所述根据所述自适应控制器，构建自适应率这一步骤中，

5.根据权利要求4所述的一种基于时变状态约束和磁滞非线性的直升机控制方法，其特征在于，所述根据所述时变障碍李雅普诺夫函数，对直升机控制系统的稳定性进行评估，具体为：

6.根据权利要求1所述的一种基于时变状态约束和磁滞非线性的直升机控制方法，其特征在于，所述对直升机控制系统进行数值仿真，具体为：

7.一种基于时变状态约束和磁滞非线性的直升机控制装置，其特征在于，包括：

8.一种电子设备，其特征在于，包括处理器以及存储器；

9.一种计算机可读存储介质，其特征在于，所述存储介质存储有程序，所述程序被处理器执行实现如权利要求1至6中任一项所述的方法。

10.一种计算机程序产品，包括计算机程序，其特征在于，所述计算机程序被处理器执行时实现如权利要求1至6任一项所述的方法。

技术总结本发明公开了一种基于时变状态约束和磁滞非线性的直升机控制方法及装置，方法包括：根据拉格朗日力学模型，构建直升机控制系统的非线性动力学方程，得到二自由度直升机系统方程；结合反步法构建时变障碍李雅普诺夫函数，得出直升机控制系统的自适应控制器；根据所述自适应控制器，构建自适应率；对构建的时变障碍李雅普诺夫函数进行更新；根据所述时变障碍李雅普诺夫函数，对直升机控制系统的稳定性进行评估，并对直升机控制系统进行数值仿真，生成评估验证结果；根据达到目标条件的所述评估验证结果，通过所述直升机控制系统对目标直升机进行控制，本发明能够提升直升机系统在实际应用中的稳定性和安全性，可广泛应用于飞行系统控制技术领域。技术研发人员：吴立华,吴辉源,白洁,李杰诚,李国豪受保护的技术使用者：广东开放大学（广东理工职业学院）技术研发日：技术公布日：2024/11/14