一种行星系统内多卫星借力燃耗最优轨道优化方法

本发明涉及一种航天器轨道优化方法，尤其涉及行星系统内多卫星借力轨道优化方法，属于航空航天。

背景技术：

1、多卫星借力轨道是深空探测任务中实现目标行星系统内低能量转移的重要途经，利用不同卫星之间的借力配合可以有效降低转移过程中航天器的燃耗。由于行星系统内卫星数量较多且运行周期较短，借力序列丰富多样，与星际转移借力轨道相比决策变量成倍增长，很难利用常规的轨道优化方法进行求解。因此，如何简化行星系统内借力轨道计算模型并提出一种快求解燃耗最优借力轨道的优化方法是目前亟待解决的问题。

2、研究利用t-rp图进行多卫星借力轨道优化可以提高轨道设计效率，降低多卫星借力复杂序列问题求解难度。t-rp图本质是将航天器可能的状态描绘在周期t和近心点半径rp关系图中，在不考虑倾角的情况下，两个参数即可确定轨道的形状。在相对借力卫星v∞一定的情况下，通过共振借力能够到达的所有状态都可以表示在图中的一条曲线上。同一个借力卫星不同的v∞对应的曲线互不相交。两个不同的借力卫星之间可能存在相交的曲线，交点对应的状态即可实现卫星间不考虑相位情况下的转移。因此如何利用t-rp图准确快速求解借力序列是多卫星借力轨道优化中需要解决的关键问题。

3、在已开展的行星系统内多卫星借力轨道优化的相关研究中，先技术[1](strangen j,longuski j m.graphical method for gravity-assist trajectory design[j].journal of spacecraft and rockets,2002,39(1):9-16.)中，提出利用t-rp图有助于评估可能存在的天体借力轨道，并指出从能量的角度来看，这样设计的轨道都是可行的。如果在t-rp图中都不存在的借力轨道那么一定是不可行的。该方法可以帮助缩减可行解搜索范围进而提高轨道设计效率，但是只适用于行星际借力转移轨道设计，且人工参与度较高。

4、先技术[2](井泉,李明涛,王有亮.木卫四探测任务转移轨迹状态序列搜索与优化[j].北京航空航天大学学报,1-14.)中，针对使用图形化分析方法在设计木卫四环绕任务转移轨道时人工参与度高的问题，提出了基于图形化分析的转移轨道状态序列搜索算法。通过对图形性质以及共振引力辅助的分析，归纳出轨道状态的变化模式，进而提出迭代求解状态转移序列的搜索算法。该方法解决了使用图形化分析方法时人工参与度高的问题，但是在实施过程中只针对图中特定曲线中特定周期对应的特征点集进行搜索，只能获得可行解而非最优解。

技术实现思路

1、为解决现有方法无法实现对行星系统内多卫星借力燃耗最优轨道进行求解，本发明的目的是提供一种行星系统内多卫星借力燃耗最优轨道优化方法，基于t-rp图推导借力参数与转移轨道状态之间的关系式，建立多卫星借力轨道参数递推模型，以不同卫星间转移轨道参数为变量，以总速度增量最小为目标函数对轨道进行优化，获得行星系统内多卫星借力燃耗最优轨道。

2、本发明的目的是通过下述技术方案实现的：

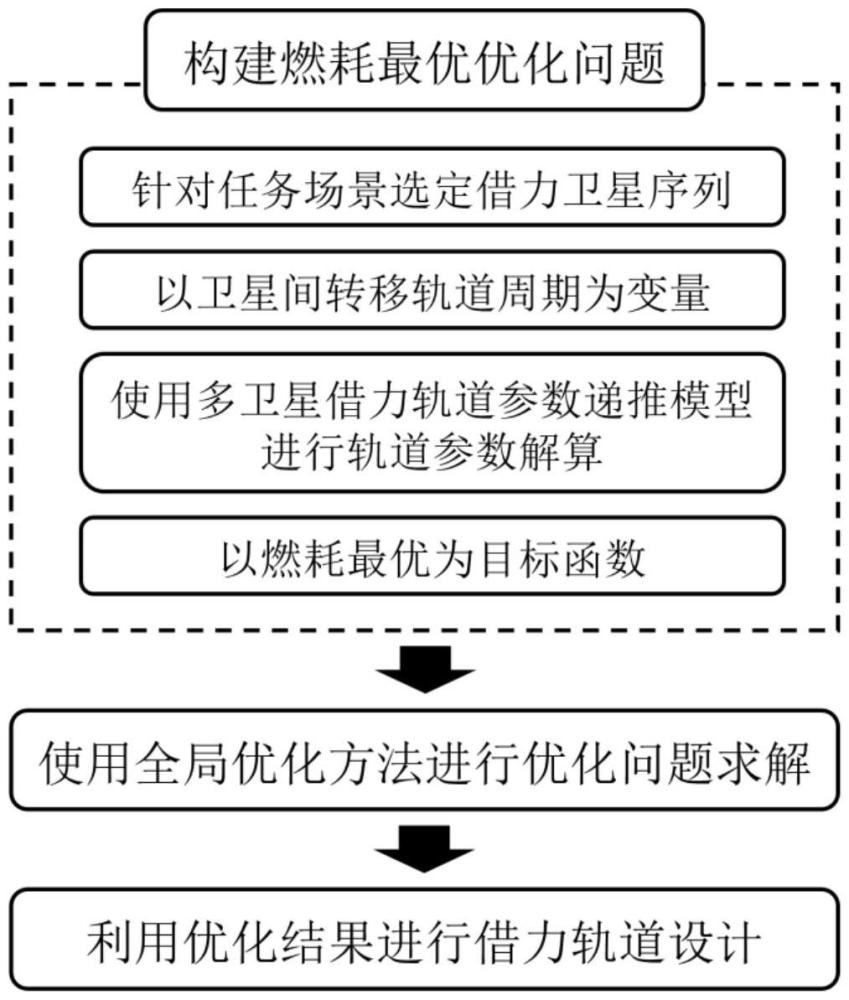
3、本发明公开的一种行星系统内多卫星借力燃耗最优轨道优化方法，选择满足探测需求的借力卫星序列，以各转移轨道周期为变量，只在离开初始轨道以及被目标卫星捕获或进入目标轨道时添加机动，优化目标为总速度增量最小，在行星质心惯性系下构建轨道优化问题。在进行优化问题求解时，根据航天器在借力卫星间转移轨道的参数可以求解下一次卫星借力时的状态，由该状态可以匹配借力后转移轨道的参数进而实现连续求解，直到得到到达目标卫星时的状态。最后采用遗传算法对该优化问题进行求解，得到抵达各借力卫星的相对速度以及借力前后的转移轨道参数，即获得行星系统内多卫星借力燃耗最优轨道，根据转移轨道参数实现参考在星历下各段转移轨道转移。

4、本发明公开的一种行星系统内多卫星借力燃耗最优轨道优化方法，包括如下步骤：

5、步骤一，初始轨道为环绕行星运行的大椭圆轨道，确定目标卫星以及该卫星的环绕圆轨道高度，选择满足探测需求的借力卫星序列，以进入首次借力卫星前转移轨道周期以及序列中相邻借力卫星之间的转移轨道周期为变量，只在离开初始轨道以及被目标卫星捕获时添加机动，优化目标为总速度增量最小，在行星质心惯性系下构建轨道优化问题；

6、初始轨道周期为t0，近心点半径为rp，0；借力卫星的序列为m1,m2,…,mn，该序列中允许存在重复的借力卫星，但是相邻的借力卫星是不同的；为了简化表达，目标卫星也算在借力卫星序列中但不参与借力，记为mn；作为变量的各转移轨道周期为t1,t2,…,tn，其中t1为从初始轨道到借力卫星m1之间转移轨道的周期，t2,…,tn分别为序列中相邻借力卫星之间转移轨道的周期；

7、整个转移轨道过程中只添加两次脉冲机动，第一次是在初始轨道远心点添加机动调整近心点高度，之后进入借力卫星m1之前的转移轨道，这次机动记为pem，第二次是在进入目标卫星环绕轨道时的插入机动，记为oim；综上，转移轨道的总速度增量估计为：

8、δvseq＝δvpem+δvoim (1)

9、其中，δvpem为远心点机动大小，δvoim为插入机动大小。

10、在优化过程中需要有两个约束条件，首先是借力序列中每一段转移轨道的周期ti都需要在卫星借力后的周期可达范围[tmin,i,tmax,i]内，另一个是出于安全考虑，每一段转移轨道的近心点半径rp,j都要高于设定的安全半径rlim；

11、在行星质心惯性系下构建轨道优化问题建模如下：

12、x＝(t1,t2,…,tn)

13、minf(x)＝δvseq

14、s.t. tmin,i≤ti≤tmax,i(i＝2,3,…,n)

15、rp,j≥rlim(j＝1,2,…,n)

16、步骤二，在初始轨道远心点添加机动，航天器进入转移轨道最终与借力卫星m1相交，根据转移轨道的周期求出转移轨道的半长轴，进而分别求出初始轨道和转移轨道的远心点速度，由速度差求解远心点机动的大小；

17、半长轴与周期关系如式(2)所示，

18、

19、式中，μ为行星引力常数；t为轨道周期；a为轨道半长轴。

20、根据式(2)，由t0和t1分别求出初始轨道半长轴a0和转移轨道半长轴a1。

21、由初始轨道半长轴a0和近心点半径rp，0求得远心点半径ra,0：

22、ra，0＝2a0-rp，0 (3)

23、转移轨道远心点与初始轨道远心点相同，即ra，1＝ra,0。

24、远心点速度公式如式(4)所示，

25、

26、式中，ra为轨道近心点半径，vra为轨道远心点速度。

27、将a0和ra,0以及a1和ra,1分别带入式(4)，求得初始轨道远心点速度vra,0和转移轨道远心点速度vra,1；

28、在远心点施加的速度增量方向为速度切向，因此求得δvpem：

29、δvpem＝|vra,1-vra,0| (5)

30、步骤三，根据到达借力卫星m1前的转移轨道参数以及借力卫星轨道参数求出航天器相对借力卫星m1的速度大小；

31、由到达借力卫星m1前的转移轨道半长轴a1和远心点半径ra，1求得偏心率e1：

32、

33、基于tisserand准则推导出式(7)，由相对借力卫星的速度状态求解转移轨道的偏心率；

34、

35、式(7)中，e为转移轨道偏心率，a为转移轨道半长轴，r为借力卫星运行轨道半长轴，v为航天器速度，v∞为航天器相对借力卫星的速度，α为v∞矢量与借力卫星速度vp矢量方向之间的夹角；

36、由式(7)推导出式(8)：

37、

38、根据航天器速度与借力卫星速度相对关系可得：

39、

40、式中，vp为借力卫星绕中心天体公转速度大小。

41、由式(9)推导出式(10)：

42、

43、联立式(8)与式(10)消去α得到：

44、

45、由a1求出航天器抵达借力卫星时的速度v1,in：

46、

47、其中，r1为借力卫星m1运行轨迹的半长轴；

48、由式(11)得到关于卫星m1借力之前的表达式：

49、

50、其中，v∞,1为航天器抵达借力卫星m1时的相对速度，vp,1为借力卫星m1绕中心天体运行的公转速度；

51、式(13)中，除了v∞,1之外的所有量均为已知量，根据式(13)得到符合条件的v∞,1；

52、步骤四，基于航天器到达借力卫星mi的相对速度v∞,i(i＝1,2,...,n-1)，通过借力模型计算得到不同借力转角对应的借力后速度状态，求得借力后轨道周期和近心点半径的映射关系，即t-rp图中借力卫星mi在v∞,i下对应的t-rp曲线；利用借力后转移轨道的周期这一变量进行插值计算，得到该转移轨道的近心点半径，进而求得转移轨道的半长轴和偏心率；根据转移轨道的参数可以求出航天器到达下一借力卫星mi+1的相对速度v∞,i+1。

53、根据式(9)得到航天器经过借力卫星mi借力之后的速度vi,out：

54、

55、由于式(14)中vp,i和v∞,i均为已知量，αout为航天器离开借力卫星mi时速度矢量方向与借力卫星mi公转速度矢量方向之间的夹角，因此vi,out表示为仅与αout有关的函数：

56、v1,out＝g(αout) (15)

57、αout在理论范围[0,2π]内任意取值；因此可以求解不同αout对应借力卫星mi后转移轨道的周期ti+1和近心点半径rp,i+1，进而得到ti+1-rp,i+1关系曲线；根据关系曲线确定ti+1取值的范围[tmin,i+1,tmax,i+1]，将变量ti+1进行插值计算得到rp,i+1。

58、由ti+1求得转移轨道半长轴ai+1：

59、

60、由rp,i+1和ai+1求得转移轨道偏心率ei+1：

61、

62、

63、式(19)中除了v∞,i+1之外的所有量均为已知量，根据式(19)得到符合条件的v∞,i+1。

64、步骤五，重复步骤四直至求解出抵达目标卫星的相对速度v∞,n；

65、步骤六，根据抵达目标卫星的v∞,n以及环绕圆轨道高度rh，求解出进入环绕轨道插入机动的大小；

66、环绕圆轨道半径rcircle表示为：

67、rcircle＝radn+rh (20)

68、其中，radn表示目标卫星的物理半径；

69、根据式(21)求解环绕圆轨道的线速度vcircle：

70、

71、其中，μn为目标卫星的引力常数；

72、航天器抵达环绕圆轨道高度时的速度vin为：

73、

74、根据式(23)求出航天器进入环绕圆轨道时插入机动δvoim：

75、δvoim＝|vcircle-vin| (23)

76、步骤七，采用全局优化算法对对轨道优化问题进行求解，得到抵达各借力卫星的相对速度v∞,i以及对应的转移轨道周期ti；在不考虑星历的情况下，通过v∞,i和ti完成各段转移轨道优化。

77、步骤八，如果通过一次借力无法实现借力前后轨道的转换，航天器通过对同一借力卫星进行多次共振借力能够实现借力前后轨道的转换。

78、有益效果：

79、1、本发明公开的一种行星系统内多卫星借力燃耗最优轨道优化方法，基于t-rp图推导借力状态与转移轨道之间正解和反解的关系式，建立多卫星借力轨道状态递推模型，利用借力序列中相邻卫星间转移轨道周期作为变量，实现已知序列的多卫星借力轨道快速求解，提高对行星系统内多卫星借力燃耗最优轨道的优化效率。

80、2、本发明公开的一种行星系统内多卫星借力燃耗最优轨道优化方法，建立行星系统内多卫星借力轨道优化模型，以各段转移轨道周期为变量求解燃耗最优的借力轨道，该方法适用于任意行星系统内多卫星借力轨道优化，具有普适性。

81、3、本发明公开的一种行星系统内多卫星借力燃耗最优轨道优化方法，选择满足探测需求的借力卫星序列，以各转移轨道周期为变量，只在离开初始轨道以及被目标卫星捕获或进入目标轨道时添加机动，优化目标为总速度增量最小，在行星质心惯性系下构建轨道优化问题，提高优化结果的收敛性且优化结果接近理论最优解。