数模联合驱动的滚动轴承剩余使用寿命预测系统及方法

本发明属于滚动轴承健康预测，尤其涉及数模联合驱动的滚动轴承剩余使用寿命预测系统及方法。

背景技术：

1、滚动轴承作为旋转机械的关键零部件，其作用是支撑旋转体，减小摩擦力，降低能量损失。在旋转机械设备中，滚动轴承故障数占比大型设备和小型设备故障总数的40-90％不等，其中内、外圈裂纹是滚动轴承最常见的故障，占滚动轴承所有故障的90％。因此滚动轴承的内外圈的健康状态与机械设备安全运转密切相关。如果滚动轴承能被及时发现和预测故障，不仅提高生产效率，还能够减少维修成本和保证工厂安全运行。因此，滚动轴承剩余使用寿命预测的研究成为迫切需求。

2、目前滚动轴承的剩余使用寿命预测方法有四大类：数理统计，物理模型，深度学习，数字孪生。基于数理统计的剩余寿命预测模型可以获得了较好的预期结论，该模型借助概率统计的原理，通过对系统运行数据的深入分析以量化剩余寿命的概率分布，但需要依靠大量的专家经验知识和实验数据才能实现。基于物理模型的滚动轴承剩余寿命预测方法精度最高，该模型利用物理规则，分析滚动轴承的失效机理以预测剩余寿命，但需要明晰滚动轴承的物理规则，同时模型只适用当前工况，适应性比较差。基于深度学习的滚动轴承剩余使用寿命预测方法被广泛应用，因为在没有考虑失效机理的情况下深度学习利用强大万能近似定理拟合出任何函数关系。然而，深度学习的黑盒特性无法解释其决策过程，同时需要大量的训练数据数量。在实际工业中，获得大量的滚动轴承全寿命周期的训练数据是困难且相对昂贵的。

3、幸运的是，得益于而仿真、传感器、计算机的发展，数字孪生方法的出现和迅速兴起为这一挑战提供了全新的解决方案。数字孪生技术能够准确地反映实际生产过程和全生命周期的运行性能，通过孪生模型进行仿真可以映射物理过程的动态演化行为。jiang等人提出了最流行的dt定义之一，提出了一个三维dt模型，该模型由现实世界的实体、虚拟实体和将这两个实体联系在一起的数据连接组成。zhao等人针对轴承等机械设备的小样本问题，利用dt获取的仿真数据集，扩大样本量，提高滚动轴承寿命预测结果的精度。为了减小模拟信号与被测信号之间的误差，提出一种改进的cyclegan方法，实现虚拟空间模拟数据与物理空间中被测数据的映射。zhang等人通过建立了高保真数字孪生模型，采用偏域自适应算法，将从数字孪生模型中学到的诊断知识转移到物理试验台的实测数据中。该方法能够利用实测数据准确诊断实际滚动轴承的健康状况。wang等使用成熟的动力学模型构建数字孪生模型，并通过pearson相关系数进行修正，这是一种模型在线学习，将轴承不同状态同步到正常运行模型中，得到正常、故障等仿真数值数据。上述模型具备快速模拟的能力，实时交互效果显著，同时保持了较好的预测精度。然而上述模型存在的共同问题：传统数字孪生需要滚动轴承全寿命实测振动信号识别缺陷尺寸，从而将不同退化阶段缺陷尺寸应用到模型才能模拟出全寿命周期信号；数字孪生模型需要当前工况下全寿命周期疲劳缺陷尺寸，传统数字孪生模型没有考虑到在自然剥落状态下的缺陷尺寸识别问题从而导致缺陷尺寸误差较大以及模型预测结果精度不高问题。

4、传统孪生模型是利用全寿命实测信号来进行全寿命周期信号模拟，模型准确性对全寿命实测信号数据量要求较高。

技术实现思路

1、针对现有技术的不足，本发明提出一种数模联合驱动的滚动轴承剩余使用寿命预测系统及方法，基于损伤力学耦合动力学生成滚动轴承内圈故障全寿命周期振动信号并利用更新模块修正振动信号以解决模型预测结果精度不高问题。

2、本发明的技术方案为：

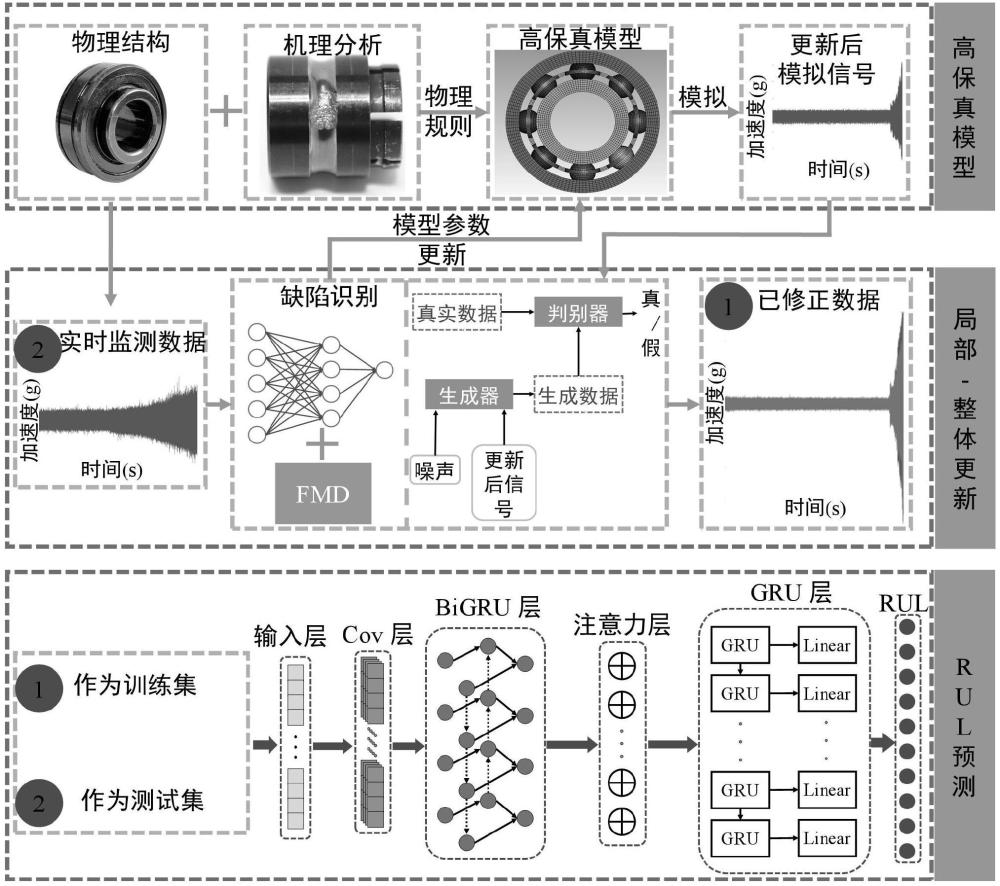
3、一方面，本发明提供数模联合驱动的滚动轴承剩余使用寿命预测系统，该系统为一个数字孪生模型，包括物理实体模块、高保真模型模块、整体更新模块、局部更新模块和剩余使用寿命预测模块；

4、所述物理实体模块用于获取实时监测的滚动轴承内圈故障的振动信号；

5、所述高保真模型模块用于利用损伤-断裂耦合理论表征滚动轴承的失效机理，结合损伤力学与动力学建立具备缺陷扩展的滚动轴承动力学模型，利用滚动轴承动力学模型生成表示滚动轴承不同退化阶段的模拟的滚动轴承内圈故障全寿命周期的振动信号；

6、所述整体更新模块用于利用递归特征模态分解算法分解实时监测的滚动轴承的内圈故障振动信号以获取滚动轴承内圈的缺陷尺寸，利用获取的滚动轴承内圈的缺陷尺寸对高保真模型模块进行更新，得到更新后的模拟的滚动轴承内圈故障全寿命周期的振动信号；

7、所述局部更新模块为cwgan-gp网络模型，用于将更新后的模拟的滚动轴承内圈故障的振动信号作为条件信息，通过生成器与判别器之间不断博弈，得到修正后的滚动轴承内圈故障全寿命周期的振动信号；

8、所述剩余使用寿命预测模块用于利用修正后的滚动轴承内圈故障全寿命周期的振动信号构建训练集对门控循环单元网络gru进行训练，并使用训练完成的门控循环单元网络gru实现剩余使用寿命的预测。

9、另一方面，本发明还提供数模联合驱动的滚动轴承剩余使用寿命预测方法，包括如下步骤：

10、步骤1：模拟滚动轴承内圈缺陷的动态演化过程，并将滚动轴承内圈缺陷的动态演化过程引入动力学模型，获取模拟的滚动轴承内圈故障全寿命周期的振动信号；

11、步骤1.1：构建滚动轴承动力学模型；

12、滚动轴承动力学模型，如公式(1)所示：

13、

14、式中，x(t)为滚动轴承沿x方向的位移，为滚动轴承沿x方向的速度，为滚动轴承沿x方向的加速度，f为径向力，m为滚动轴承的质量，q为滚动轴承总刚度，c为滚动轴承总阻尼，t为时刻；所述x方向为滚动轴承径向或轴向；

15、步骤1.2：采用abaqus的扩展有限元法构建内圈疲劳剥落演化模型；

16、步骤1.2.1：根据赫兹接触理论计算滚动轴承的接触应力；

17、步骤1.2.2：简化滚动轴承的滚动体与内圈结构为具有等效半径的滚动体以相对速度与内圈表面进行接触并在半无限平面上滚动，利用abaqus创建简化部件，实现滚动轴承的滚动体接触内圈的真实状态的模拟；

18、进一步地，在利用abaqus创建简化部件时假设滚动轴承各组件材料处于无损状态，网格单元损伤设为0；

19、步骤1.2.3：使用预先计算的滚动轴承的接触应力采用沿滚动轴承的内圈表面移动的方法等效滚动体的滚动过程，实现循环载荷的设置；

20、步骤1.2.4：将损伤变量引入到线弹性应力应变本构方程中，利用线弹性应力应变本构方程模拟材料疲劳破坏时的力学性能，并计算当前循环载荷下网格单元的剪切应力；

21、引入损伤变量的线弹性应力应变本构方程如式(2)所示：

22、σ＝j(1-d)ε(2)

23、式中，σ为剪切应力，j为材料刚度，ε为应变，d为损伤变量；

24、步骤1.2.5：采用损伤演化方程计算滚动接触域内各网格单元的损伤演化率；所述滚动接触域为滚动轴承的滚动体的滚动接触范围；

25、所述损伤演化方程如式(3)所示：

26、

27、式中，n为循环载荷的总循环次数，a为修正系数，τ，m为通过轴承钢材料疲劳裂纹扩展速率试验确定的参数，δτ为应力幅；

28、步骤1.2.6：根据滚动轴承内圈材料属性，设定滚动轴承内圈损伤为线弹性损伤累计，根据各网格单元的损伤演化率，计算每个网格单元的损伤值；

29、损伤值的计算方法如式(4)所示：

30、

31、其中，为第j个网格单元在第b次循环时的损伤值，为第j个网格单元在第b-1次循环时的损伤值，为第j个网格单元在第b次循环时的损伤演化率，δnb为当前的循环次数；

32、步骤1.2.7：使用abaqus中的扩展有限元xfem，对随着循环载荷的循环次数增加而增加的疲劳损伤累积进行数值模拟，模拟裂纹萌生和裂纹扩展的过程，当网格单元的损伤值达到临界损伤值时，认定该网格单元失效，记录此时循环载荷的循环次数及失效的网格单元的位置和尺寸，并去除因失效的网格单元导致剥落的网格单元，持续施加循环载荷，直至失效的网格单元扩展到滚动轴承内圈表面时，滚动轴承认定为完全失效，得到疲劳剥落演化模型；

33、步骤1.3：提取疲劳剥落演化模型中失效的网格单元的位置和尺寸，计算滚动体总变形量；计算滚动体总变形量的方法为：

34、ψ＝xcosαz+ysinαz-γ-s(t)(5)

35、式中：ψ为滚动体总变形量，s(t)为滚动体经过缺陷时的位移，x为滚动体经过缺陷时的周向方向的位移，y为滚动体经过缺陷时的径向方向的位移，αz为第z个滚动体与径向方向的夹角，γ为轴承间隙；

36、步骤1.4：计算每个循环中的滚动体总变形量，并将每个循环中的滚动体总变形量引入滚动轴承动力学模型，基于四阶龙格库塔法计算振动信号，获得不同退化阶段的振动信号并将不同退化阶段的振动信号组合，得到模拟的滚动轴承内圈故障全寿命周期的振动信号；

37、步骤2：获取实时监测的滚动轴承内圈故障的振动信号；

38、步骤3：利用递归特征模态分解算法分解实时监测的滚动轴承内圈故障的振动信号，以识别滚动轴承内圈的缺陷尺寸；

39、步骤3.1：加载实时监测的滚动轴承内圈故障的振动信号；

40、步骤3.2：初始化迭代次数k＝1，并设置第k次迭代的初始信号为xk(t)；

41、进一步地，当k＝1时初始信号为步骤3.1中加载的实时监测的滚动轴承内圈故障的振动信号；

42、步骤3.3：通过hanning窗口初始化有限脉冲响应滤波器组；所述有限脉冲响应滤波器组中包括若干个有限脉冲响应滤波器；

43、步骤3.4：使用有限脉冲响应滤波器组对初始信号进行滤波，得到若干个分解模态；

44、滤波方法为：

45、uk(t)＝xk(t)*fk(6)

46、其中，uk(t)为分解模态，*为卷积运算，fk为有限脉冲响应滤波器；

47、步骤3.5：根据初始信号xk(t)、分解模态uk和设定的初始估计周期tk更新有限脉冲响应滤波器组中有限脉冲响应滤波器的系数；

48、步骤3.6：根据分解模态计算分解模态之间的相关系数进而构建相关矩阵；

49、所述相关系数的计算方法为：

50、

51、式中，cc为相关系数，up、uq为两组模态，每组模态中包括如干个分解模态，up(r)为up中的第r个分解模态，uq(r)为uq中的第r个分解模态，为up(r)的平均值，为uq(r)的平均值模态总数，r为分解模态总数；

52、步骤3.7：从相关矩阵中选出最大的两个相关系数对应的分解模态并计算其相关峰度，选择最大的相关峰度作为递归特征模态分解算法的模态分量；

53、步骤3.8：计算残余信号并将其作为新的初始信号：

54、所述残余信号为：

55、xk+1(t)＝xk(t)-uk(t)(8)

56、其中，xk+1(t)为残余信号；

57、步骤3.9：根据新的初始信号利用停止准则判断是否达到停止条件，若是则输出当前的模态分量，否则当前迭代次数+1并返回步骤3.4；

58、所述停止准则为：

59、

60、其中，为第k-1次迭代时的模态分量，为第k次时的模态分量，为设定的阈值；

61、步骤3.10：利用模态分量的波形特征获取滚动轴承滚动体进入缺陷和退出缺陷的时间间隔，并计算滚动轴承内圈的缺陷尺寸；

62、

63、其中，υ为滚动轴承内圈的缺陷尺寸，t为滚动轴承滚动体进入缺陷和退出缺陷的时间间隔，n为滚动轴承的转速，为滚动轴承内圈内径；

64、步骤3.11：重复步骤3.1至步骤3.10，直至得到全部实时监测的滚动轴承内圈故障的振动信号对应的滚动轴承内圈的缺陷尺寸；

65、步骤4：利用径向基函数网络rbf对高保真模型的内圈缺陷尺寸进行更新，得到更新后的模拟的滚动轴承内圈故障全寿命周期的振动信号；

66、步骤4.1：获取滚动轴承内圈缺陷尺寸样本集其中表示获取的缺陷尺寸对应的滚动轴承全寿命周期的振动信号时间；

67、步骤4.2：利用滚动轴承内圈缺陷尺寸样本集训练径向基函数网络rbf，得到训练完成的径向基函数网络rbf；

68、步骤4.3：将步骤3.11得到的滚动轴承内圈的缺陷尺寸输入到训练完成的径向基函数网络rbf，得到未来一段时间内的滚动轴承内圈的缺陷尺寸的预测值；

69、步骤4.4：根据不同时间的滚动轴承内圈的缺陷尺寸的预测值利用二项式拟合构建滚动轴承内圈缺陷尺寸趋势函数，并利用滚动轴承内圈缺陷尺寸趋势函数得到全周期的滚动轴承内圈缺陷尺寸；

70、步骤4.5：将得到的全周期的滚动轴承内圈缺陷尺寸带入到公式(5)和公式(1)对高保真模型进行更新，得到更新后的模拟的滚动轴承内圈故障全寿命周期的振动信号；

71、步骤5：利用cwgan-gp网络模型对更新后的模拟的滚动轴承内圈故障全寿命周期的振动信号进行修正，得到修正后的滚动轴承内圈故障全寿命周期的振动信号；

72、步骤5.1：利用余弦相似度法寻找更新后的模拟的滚动轴承内圈故障全寿命周期的振动信号中不同退化阶段的模拟的滚动轴承的振动信号对应的实时监测的滚动轴承内圈故障的振动信号；

73、步骤5.2：设置cwgan-gp网络模型的参数，将更新后的模拟的滚动轴承内圈故障的振动信号作为条件信息，实时监测的滚动轴承内圈故障的振动信号作为真实样本，训练cwgan-gp网络模型直至达到设定训练轮次，得到训练完成的cwgan-gp网络模型并输出的修正后的滚动轴承内圈故障全寿命周期的振动信号；

74、步骤6：利用修正后的滚动轴承内圈故障全寿命周期的振动信号构建训练集对门控循环单元网络gru进行训练，并使用训练完成的门控循环单元网络gru实现剩余使用寿命的预测；

75、步骤6.1：利用得到修正后的滚动轴承内圈故障全寿命周期的振动信号构建带标记的数据{xt,yt}作为训练集中的训练数据，其中xt为修正后的滚动轴承的振动信号，yt为时间标签；

76、步骤6.2：利用卷积层提取修正后的滚动轴承内圈故障全寿命周期的振动信号的特征，得到大小为的特征值向量

77、步骤6.3：利用特征值向量对门控循环单元网络gru进行训练得到训练完成的门控循环单元网络gru；

78、步骤6.4：获取当前的实时监测的滚动轴承内圈故障的振动信号输入训练完成的门控循环单元网络gru，得到预测的健康值，进而得到剩余使用寿命的拟合值；

79、轴承的剩余使用寿命定义为预测的未来退化状态首次达到失效阈值的时间与当前时间的时间间隔；

80、通过采用多项式拟合预测模型输出的健康曲线，实现轴承剩余使用寿命预测，计算公式如下：

81、

82、式中，hi为健康值，tu为记录时间，ωu和ξ为拟合参数，u为拟合总项数，u为拟合项的编号。

83、与现有技术相比较，本发明的有益效果为：

84、(1)基于损伤-断裂耦合理论的滚动轴承疲劳剥落演化模型可以较好地描述轴承内圈疲劳损伤在全寿命周期内的演化规律，在此基础上，引入疲劳剥落演化模型中演化缺陷至滚动轴承动力学模型，以建立轴承内圈剥落故障的高保真模型。

85、(2)在轴承内圈自然剥落的情况下，基于递归特征模态分解算法对滚动轴承实时振动信号进行分解以识别出缺陷的尺寸，解决传统数字孪生模型只能识别滚动轴承人工缺陷下缺陷尺寸的问题。

86、(3)利用cwgan-gp网络模型对实时信息与模拟信息进行交互，采用全寿命周期的内圈缺陷尺寸更新高保真模型的位移激励，从而实现数字孪生的局部到整体动态“更新”。

87、(4)采用门控循环单元网络gru实现轴承退化状态追踪和剩余使用寿命预测。

88、综上所述，本发明考虑裂纹开裂特征并引入损伤变量概念以模拟内圈缺陷尺寸的演化历程，用于获得滚动轴承内圈故障的全寿命周期精准振动信号。所提模型只需要实时监测数据，避免了传统孪生模型对当前工况下全寿命周期实测振动信号需求。与此同时，在自然剥落情况下滚动轴承缺陷边缘时而粗糙、时而平滑，将引起滚动体进入/退出特征信号不一致且通常较弱，进而导致缺陷尺寸难以精准识别。本发明采用改进的特征模态分解法对滚动轴承的振动信号进行有效分解故障特征以及噪音，实现自然剥落状态下滚动轴承内圈缺陷尺寸高精度识别。