基于高阶MUSIC正交联合约束的多通道声源分离方法

本发明涉及声音处理，具体来说是基于高阶music正交联合约束的多通道声源分离方法。

背景技术：

1、在2009年alexey ozerov首次提出多通道非负分解，引入声源位置信息，提出了一个用于表示多通道音频的框架，自此拉开了多通道非负矩阵分解研究的序幕，为众多学者带来了许多灵感。实验显示，基于多通道非负矩阵分解音频具有良好的分离效果。2011年naqvism等人提出基于波束形成的多模态盲源分离算法，该算法利用波束成形，为盲源分离算法提供信号先验信息，提高了算法的分离效果。

2、2020年kouhei swkiguchi和aditya arie nugraha介绍了一种基于源的独立性、低等级性和指向性的高速盲源分离算法。2021年葛宛营在声学学报上发表的文章中提出的噪声情况下采用稀疏非负矩阵分解与深度吸引子网络的人声分离算法。实验结果表明，引入稀疏性约束可以增加非负矩阵分解的稀疏程度，稀疏程度的增加降低了运算时间。而引入声源位置信息，为盲源分离算法提供信号先验信息，更一步提高了算法的分离效果。

3、因此，如何将高阶music与正交联合约束结合起来通过提高稀疏度和增加先验信息优化多通道非负矩阵的分离性能已经成为急需解决的技术问题。

技术实现思路

1、本发明的目的是为了解决现有技术中传统声压传感器在高斯噪声背景下分离效果急剧下降以及阵列孔径的相关问题上存在限制的缺陷，提供一种基于高阶music正交联合约束的多通道声源分离方法来解决上述问题。

2、为了实现上述目的，本发明的技术方案如下：

3、一种基于高阶music正交联合约束的多通道声源分离方法，包括以下步骤：

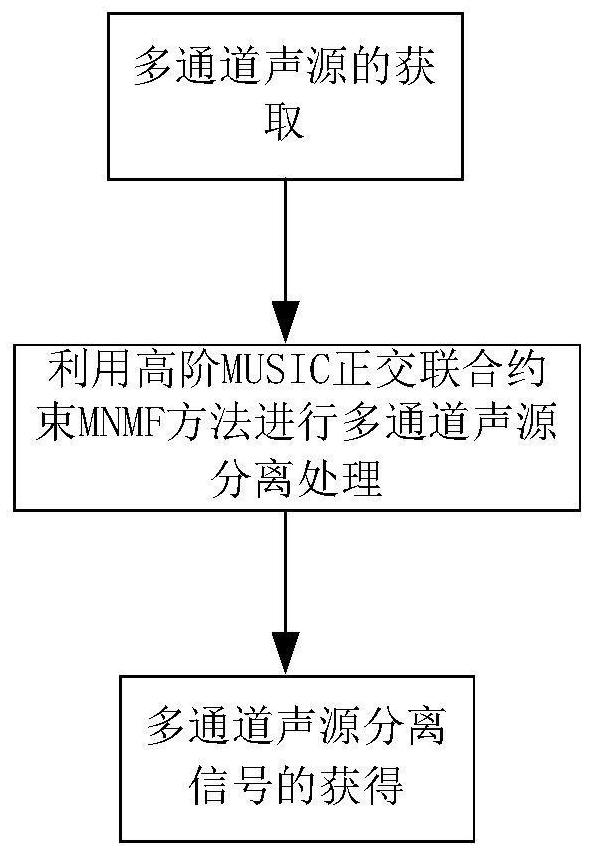
4、11)多通道声源的获取：获取多通道观测声源信号并进行预处理，生成时域观测信号；

5、12)利用高阶music正交联合约束mnmf方法进行多通道声源分离处理：对获取的时域观测信号进行短时傅里叶变换，并对获得的短时傅里叶变换矩阵进行非负预处理，再对预处理后的信号进行因子相乘获得空间相关矩阵，通过高阶引入空间特性矩阵获得空间相关矩阵的估计的因式分解式；通过is散度度量观测信号空间相关矩阵与估计空间相关矩阵之间距离，通过最小化两者之间距离，求出目标函数最小值，得到估计值，即更新后的空间相关矩阵估计

6、13)多通道声源分离信号的获得：将估计值代入多通道维纳滤波，得到分离信号。

7、所述利用高阶music正交联合约束mnmf方法进行多通道声源分离处理包括以下步骤：

8、21)对时域观测信号做短时傅里叶变换，按照式(1)进行非负处理：

9、

10、其中，sign(·)为符号函数，式中xilm为第m通道观测信号在频率i时间l下的的短时傅里叶变换，|·|1/2绝对值的平方根，[·]t为转置，为观测信号在频率i时间l下做短时傅里叶变换幅度平方根后非负处理结果；

11、22)将该信号向量的空间相关矩阵xil，表达为：

12、

13、其中，为观测信号在频率i时间l下做短时傅里叶变换幅度平方根后非负处理结果，xil为空间相关矩阵，h为共轭转置；

14、23)通过高阶music算法计算出声源的相位角θ1、θ2：

15、基于四阶累积量矩阵的music算法表示为

16、

17、

18、其中，为噪声矩阵的共轭转置，a(θ)为导向矢量，a*(θ)为导向矢量共轭，||·||2为l2范数，p(θ)为高阶music算法的空间谱公式，θ为源信号角度，是以最小优化搜索波峰得到；

19、24)将空间特性矩阵hip初始化为维度m×m的矩阵，其元素为导向矢量计算获得；

20、25)在源分离任务中，假设源信号的位置不变，难以获得源信号的精确位置信息，故引入空间特性矩阵hip，得到空间相关矩阵的估计为其表达式如下：

21、

22、其中，hip是空间特性矩阵，表示在频率i处第p个源信号，其中zpk≥0,∑pzpk＝1；

23、如果zpk接近1，则表示第k个基对应第p个源信号的概率大,zpk为第p个源对应第k个基的基础向量，其中tik列向量表示源信号幅度谱，对应行向量vkl表示在每stft帧的增益，为空间相关矩阵的估计值；

24、26)将正交联合约束引入到代价函数的基矩阵和系数矩阵中，xil为空间相关矩阵由步骤22)得出，为空间相关矩阵估计由步骤25)得出，将高阶music正交联合多通道非负矩阵分解整理为优化问题，得到目标函数：

25、

26、

27、其中，λ1、λ2、α1、α2为正则化参数，i为单位矩阵，tr(g)为矩阵的迹，det为行列式，t为基矩阵，v为系数矩阵，xil为频率为i时间为l的空间相关矩阵，为频率为i时间为l的空间相关矩阵的估计值，f(·)为目标函数，d*(·)为度量准则，取is散度，用来计算空间相关矩阵和空间相关矩阵估计之间距离，||·||1为l1范数，||·||f为frobenius范数，[·]t为转置；

28、27)定义辅助函数，求解参数更新，通过下式得到：

29、

30、其中，λ1、λ2、α1、α2为正则化参数，i为单位矩阵，tr(·)为矩阵的迹，det为行列式，t为基矩阵，v为系数矩阵，xil为频率为i时间为l的空间相关矩阵，为频率为i时间为l的空间相关矩阵估计，hip为空间特性矩阵，rilp和uil为满足正定性的辅助变量，其中i为频率、l为时间、p为声源数，zpk为第p个源对应第k个基的基础向量，其中tik列向量表示源信号幅度谱，对应行向量vkl表示在每stft帧的增益，||·||1为l1范数；

31、28)通过最小化辅助函数得到高阶music正交联合约束多通道非负矩阵分解的更新规则，根据公式分别迭代更新参数tik,vkl,zpk，hip；

32、正交联合约束mnmf的更新规则如下：

33、

34、

35、

36、其中，λ1、λ2、α1、α2为正则化参数，tr(·)为矩阵的迹，t为基矩阵，v为系数矩阵，xil为频率为i时间为l的空间相关矩阵，为频率为i时间为l的空间相关矩阵估计，hip为空间特性矩阵，其中i为频率，l为时间，p为声源数，rilp和uil为满足正定性的辅助变量，tik为信号源在频率i下的基数k的幅值，vkl为信号源在时间i下的基数k的短时傅里叶变换帧增益。迭代更新获得的参数tik,vkl,zpk；

37、29)更新后的空间特性矩阵hip代入25)步获得更新的空间相关矩阵估计

38、所述将空间特性矩阵hip初始化为维度m×m的矩阵包括以下步骤：

39、31)通过将高阶music算法估计出来的入射角度θ1、θ2代入h获得导向矢量h，其公式如下：

40、h＝[1,e-j(2πf/c)dsinθ]                 (4)

41、上式中d为阵列之间间距，θ为入射方向角，f为信号频率，在此使用两个源信号，故有θ1、θ2两个相位角；

42、32)通过将导向矢量的表达式带入到空间特性矩阵表达式中，即获得hip初始化值，

43、hip＝hhh+∈iki                         (5)

44、式中，∈为较小值，i为单位矩阵，大小为m×m，hh为导向矢量，大小为m×1，∈ik为任意值的较小正数。

45、有益效果

46、本发明的基于高阶music正交联合约束的多通道声源分离方法，与现有技术相比提出了高阶多重信号分类(music)正交联合约束的多通道非负矩阵分解算法，针对复杂环境中高斯噪声的干扰，通过高阶累计量的music算法，获得声音信号精确地方位信息，将声源信号方位信息引入到多通道非负矩阵模型中，为空间协方差矩阵提供了先验信息，提高了声音的分离效果。同时，通过对多通道非负矩阵模型中基矩阵和系数矩阵进行正交联合约束，提高多通道非负矩阵分解整体的稀疏性，得到更好的信号特征，提高声信号分离性能。