一种基于改进径向基函数的钢筋下料成本及效率的优化方法及装置与流程

一种基于改进径向基函数的钢筋下料成本及效率的优化方法及装置，用于钢筋下料优化，属于施工成本管理。

背景技术：

1、随着建筑业的热度逐渐冷却，建筑市场的竞争日趋激烈，利润空间的收缩导致许多建筑企业举步维艰。施工方不仅需要具备雄厚的技术实力和经济实力，同时还要具备科学管理的能力。在合理范围内，为了追求最大限度的成本节约，需要不断优化项目成本，并对其进行严格控制。钢筋作为建筑设计、施工和造价的关键组成部分，其造价占项目总造价的30％至40％。因此，对钢筋下料优化的研究对企业具有巨大的经济利益。

2、在钢筋下料优化领域，通常采用经验丰富的工人制定钢筋下料单，存在以下问题：受人工因素的影响，在制定每日钢筋下料剪裁任务时，会造成不同程度的钢筋资源浪费；自动化程度低，一项下料工作的完成需要多人共同配合完成，增加了工程用人成本。

3、现有的钢筋下料优化问题的处理方案的算法模型对大规模问题处理能力较差，受限于计算量和迭代次数，算法模型对大规模问题的处理效率十分有限，同时也有可能因为内存限制而无法处理大规模问题。另外，现有的钢筋下料方案优化均是仅以钢筋利用率最高为目标，没有考虑施工现场的工作效率的优化方案，与实际工程需求存在一定的不匹配。

4、综上所述，现有钢筋下料优化方法存在如下技术问题：

5、1.仅以钢筋利用率最高为目标，没有考虑施工现场的施工效率，从而造成与实际工程需求匹配度低的问题；

6、2.受限于计算量、迭代次数和内存限制，对大规模问题处理能力较差，从而造成处理效率低；

7、3.当前的下料优化模型过于依赖对初始种群的设置，对种群大小、交叉概率、变异概率的设置要求较高，在不同工作情景中的适用性较差，难以满足梁场的钢筋下料方案的生成需求。

技术实现思路

1、本发明的目的在于提供一种基于改进径向基函数的钢筋下料成本及效率的优化方法及装置，解决现有技术仅以钢筋利用率最高为目标，没有考虑施工现场的施工效率，从而造成与实际工程需求匹配度低的问题。

2、为了实现上述目的，本发明采用的技术方案为：

3、一种基于改进径向基函数的钢筋下料成本及效率的优化方法，包括如下步骤：

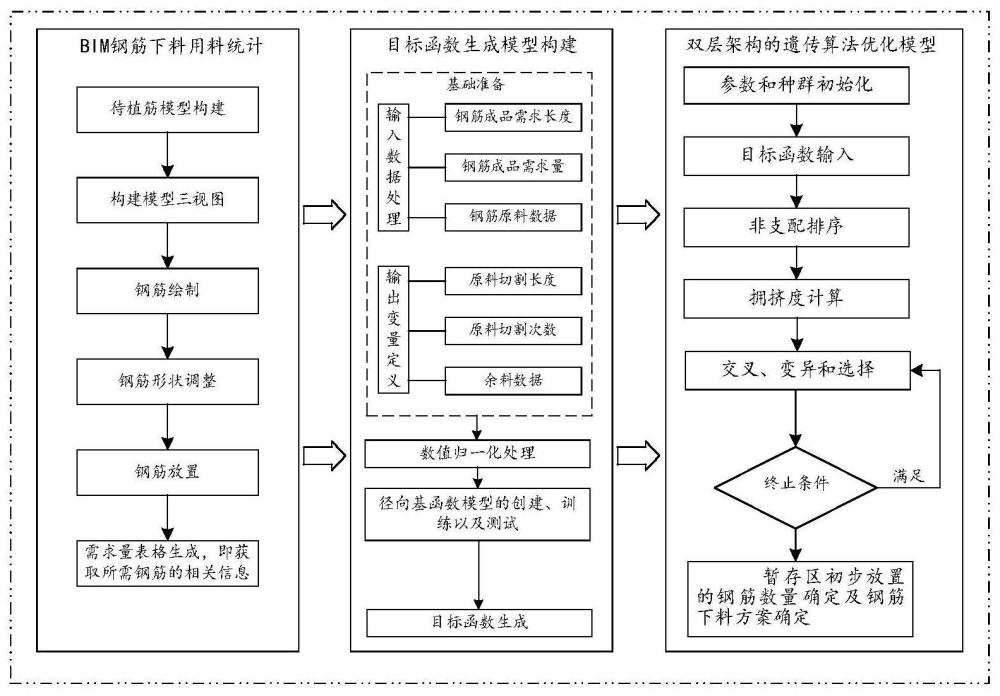
4、步骤s1、基于设计图纸和bim技术建立钢筋三维模型，钢筋三维模型建立后提取所需钢筋的相关信息，包括钢筋尺寸、数量、长度、体积和质量；

5、步骤s2、分析钢筋下料优化的因素，确定钢筋下料各因素的权重，其中，因素包括钢筋下料的余料数量、钢筋下料的切割次数和钢筋下料的焊接次数；

6、步骤s3、依据各因素的权重，确定线性叠加处理的径向基函数模型；

7、步骤s4、将确定的径向基函数模型作为遗传算法优化模型的目标函数，将不同组合的钢筋和各钢筋需求量清单输入遗传算法优化模型迭代计算，获得满足钢筋三维模型中钢筋总用量最少且施工效率最佳优化目标的钢筋下料方案。

8、进一步，所述步骤s2的具体步骤为：

9、步骤s2.1、获取已有钢筋下料切割方案，所述切割方案包括钢筋需求量、钢筋原料数量、余料数量、钢筋下料的切割次数和钢筋下料的焊接次数，以及钢筋完成加工所用的时间；

10、步骤s2.2、采用聚类算法对钢筋下料切割方案中的数据进行聚类处理，处理后统计聚类算法得到的簇，并根据各簇中各因素的分布情况和簇间的差异程度来解释各因素的重要性，即获取各因素的权重。

11、进一步，所述步骤s2.2中根据各簇中各因素的分布情况和簇间的差异程度来解释各因素的重要性的具体步骤为：

12、步骤s2.21、聚类结果可视化：

13、采用可视化方法将聚类算法得到的簇进行可视化，可视化方法包括散点图可视化方法；

14、步骤s2.22、因素分布分析：

15、对于每个簇，计算该簇中各个因素的统计量得到对应因素的分布情况，其中，因素的统计量包括因素在该簇中的均值和方差，通过比较不同簇中因素的分布情况，初步判断因素的重要性；

16、步骤s2.23、簇间差异度量：

17、计算不同簇之间的差异度量；

18、步骤s2.24、因素权重确定：

19、根据各因素在各簇的分布情况和簇间的差异度量，为每个因素分配一个权重，其中，越大的权重表示该因素在聚类结果中具有越大的重要性或区分度；

20、步骤s2.25、基于标度法判断各因素的权重是否满足要求，若满足，即得到正确的权重，否则，调整步骤2.1中的钢筋下料切割方案，重新计算权重。

21、进一步，所述步骤s3中的径向基函数模型包括3个径向基函数，每个径向基函数包括对输入变量进行归一化处理的归一化函数和对归一化函数处理得到的结果进行处理的隐含层，每个径向基函数的输出为φ_i(x)；

22、归一化函数为：

23、

24、其中，k为归一化后的值，x为被归一化的数据，包括钢筋需求长度、钢筋需求质量和钢筋原材料长度，xmax、xmin分别为被归一化数据中的最大值和最小值；

25、隐含层的神经元个数的计算公式为：

26、

27、其中，n、l分别为输入神经元的个数和输出神经元的个数，a的取范围为1～10；

28、3个径向基函数线性叠加的形式为：

29、f(x)＝w_1*φ_1(x)+w_2*φ_2(x)+w_3*φ_3(x)

30、其中，w_1、w_2、w_3分别表示线性叠加中依据各因素的权重获取的各径向基函数的权重。

31、进一步，所述步骤s4的具体步骤为：

32、步骤s4.1、基于目标函数和钢筋下料在实际施工中的流程，设计对应的遗传算法优化模型，即考虑钢筋库存区、加工区和供需量的变化特点，设计双层嵌套算法，包括上层、中间层、下层和目标函数，运行顺序为上层、中间层、下层和目标函数，其中，钢筋下料在实际施工中的流程为将钢筋库存区的钢筋运送至存放区作为每天或每周的用量，存放区的钢筋分批次运送至加工区所对应的暂存区，然后逐个加工，变化特点是指在供需量为每天的钢筋加工量情况下，根据每日加工量，调配钢筋进入加工区，每次进入加工区的钢筋量需要满足加工区的存储能力和生产效率；

33、所述上层为下料方案层，用于根据不同组合的钢筋和各钢筋需求量清单决定放入排样池的钢筋的顺序和数量；

34、所述中间层为排样池，用于基于下料方案层决定放入的钢筋数量生成每个加工设备的暂存区初步放置的钢筋的顺序和数量；

35、所述下层为排样层，用于生成具体的钢筋切割及焊接方案，同时基于每个加工设备的暂存区放置的钢筋数量构建启发式规则决策各钢筋需求量订单需要加工钢筋的长度，即用于获得满足钢筋总用量最少且施工效率最佳优化目标的钢筋下料方案，具体步骤为：

36、步骤s4.11、基于各钢筋需求量订单中的钢筋数量计算加工区所有待加工钢筋数量ns，即其中，nip表示第i个钢筋需求量订单初步需要配置到所对应第p个加工区的钢筋数量；

37、步骤s4.12、基于所有待加工钢筋数量ns和获取的所有钢筋需求量订单中钢筋的总长度ls，计算各钢筋需求量订单中各钢筋的平均长度ls，公式为：

38、ls＝ls/ns；

39、步骤s4.13、计算各钢筋需求量订单所需加工钢筋的平均长度lr，公式为：

40、lr←([nip×ls])

41、其中，←表示赋值；

42、步骤s4.14、获取各钢筋需求量订单所需钢筋长度，并基于各钢筋需求量订单所需钢筋长度从大到小排列各钢筋需求量订单，同时根据排列初始化钢筋需求量订单的计数变量r＝1；

43、步骤s4.15、基于当前钢筋需求量订单r所需加工的钢筋的平均长度lr，计算当前钢筋需求量订单r的钢筋采用最小段差原则阶段后产生的段差损失r，公式为：

44、r＝la-lr

45、其中，la为钢筋需求量订单r中钢筋的总长度：

46、步骤s4.16、如果r>给定的平均置换损失×r，则将当前钢筋需求量订单中的最后一根钢筋配置在下一钢筋需求量订单中进行加工，先更新放入暂存区的钢筋数量，并根据顺序将钢筋放入暂存区，再将钢筋配置到加工区中进行加工，如果r<给定的平均置换损失×r，暂存区的钢筋数量保持不变，并根据顺序将钢筋放入暂存区，再将钢筋配置到加工区中的暂存区中进行加工；

47、步骤s4.17、如果r值超过钢筋需求量订单总数，则结束，否则跳转回到步骤s4.15，同时将下一钢筋需求量订单作为当前钢筋需求量订单，同时r＝r+1；

48、步骤s4.2、将不同组合的钢筋输入遗传算法优化模型迭代计算，获得满足钢筋三维模型中钢筋总用量最少且施工效率最佳优化目标的钢筋下料方案。

49、进一步，所述下料方案层通过遗传算法优化模型中的单链编码遗传算法求解各需求量清单中放入排样池的钢筋的顺序和数量；

50、排样层通过遗传算法优化模型中的单链编码遗传算法求解生成具体的钢筋切割及焊接方案。

51、进一步，所述遗传算法优化模型中线性规化方法的公式为：

52、

53、s.t.

54、

55、cip≥0

56、其中，cip为钢筋需求量订单i在加工区p处的钢筋数量，b表示切割次数，s.t.表示遗传算法的约束条件。

57、一种基于改进径向基函数的钢筋下料成本及效率的优化装置，包括：

58、钢筋信息提取模块：基于设计图纸和bim技术建立钢筋三维模型，钢筋三维模型建立后提取所需钢筋的相关信息，包括钢筋尺寸、数量、长度、体积和质量；

59、因素权重确定模型：分析钢筋下料优化的因素，确定钢筋下料各因素的权重，其中，因素包括钢筋下料的余料数量、钢筋下料的切割次数和钢筋下料的焊接次数；

60、径向基函数模型构建模块：依据各因素的权重，确定线性叠加处理的径向基函数模型；

61、钢筋下料方案优化模块：将确定的径向基函数模型作为遗传算法优化模型的目标函数，将不同组合的钢筋和各钢筋需求量清单输入遗传算法优化模型迭代计算，获得满足钢筋三维模型中钢筋总用量最少且施工效率最佳优化目标的钢筋下料方案。

62、与现有技术相比，本发明的优点在于：

63、一、本发明能够高效给出满足钢材利用率最高，且施工效率最高的钢筋下料方案，试验验证结果表明：本技术提出的钢筋下料优化模型在实际工程的探索应用中有可行性和应用价值，在保证钢筋加工效率的同时，钢筋利用率能够保持在98％左右，明显优于人工计算得到钢筋利用率，有助于提高现场施工质量，并减少钢筋浪费。

64、二、本发明基于bim模型和优化算法，以钢筋利用率和钢筋下料施工效率为优化目标，通过以径向基函数生成遗传算法的目标函数，实现对遗传算法目标函数和边界条件的自动化确定，保障算法模型计算的高效性和准确性，实现与现场需求的有力对接，能够有效的解决现有算法模型计算效率低，目标函数单一等问题；

65、三、本发明中的钢筋下料优化方法能够通过二次系统框架的方式集成在各类数据驾驶舱和管理平台中，可以以流程应用的形式有效推广落地，随着数字化技术的不断发展和数字孪生系统的日益完善，优化模型(钢筋下料优化方法)能够与相关系统表现出较好的适配性，并可以与更多的材料优化问题结合，形成普适性的材料管控与使用方案优化系统，将支持各类复杂工况与环境下的材料用量管控，为施工全生命周期一体化管理奠定基础。