一种基于重复控制器的五轴机床旋转轴跟踪误差补偿方法

本发明涉及数控机轴误差补偿，尤其涉及一种基于重复控制器的五轴机床旋转轴跟踪误差补偿方法。

背景技术：

1、五轴机床通常用于多角度和多方向的加工，如航空航天零部件、医疗器械等领域。pid控制器在五轴机床的旋转轴上广泛应用于制造业，特别是在精密加工和复杂零部件制造中。pid控制器具有稳定性好、易调节、结构简单等优点，目前的跟踪误差控制策略主要是使用pid控制器来减小跟踪误差。

2、pid控制器常用于实现旋转轴的姿态(角度)控制，确保机床工具在所需的角度上精确停留。在五轴加工中，pid控制器可用于轨迹追踪，确保工具沿着复杂的三维轨迹移动，以完成零部件的加工。控制旋转轴的旋转速度是五轴机床的重要任务之一，pid控制器可用于实现速度控制，确保旋转轴以期望速度旋转。在实际制造中，机床系统可能面临各种干扰，pid控制器需要具备一定的抗干扰能力，以保持系统的稳定性和精度。

3、pid控制器包括比例(proportion)、积分(integration)、微分(differentiation)部分。比例(p)表示控制旋转轴的角度误差，使其与期望值之间保持比例关系。增大比例增益可加快响应速度，但可能引入过冲。积分(i)表示对积分项的累加可处理系统稳态误差，确保系统稳定，积分控制可抑制静态误差。微分项(d)可抑制振荡，控制角度变化速率，有助于减小过冲，提高系统的动态响应。

4、在五轴机床的系统中，pid控制器可能导致过冲，即实际输出超过了期望值，然后再次回到期望值，这可能会导致机床系统产生震荡。pid控制器对系统参数变化较为敏感。当五轴机床系统的工作条件、负载或其他参数发生变化，pid控制器可能需要重新调整参数以适应这些变化。五轴机床是复杂的多自由度系统，其动力学特性较为复杂。pid控制器不适用于复杂系统，可能不足以提供良好的性能。pid控制器设计基于线性系统模型，对于非线性系统可能表现不佳。五轴机床旋转轴的运动通常涉及到周期性的姿态或位置误差，例如机械振动、传动系统的非理想性等，因此需要更复杂的控制策略。

技术实现思路

1、基于上述目的，本发明提供了一种基于重复控制器的五轴机床旋转轴跟踪误差补偿方法。

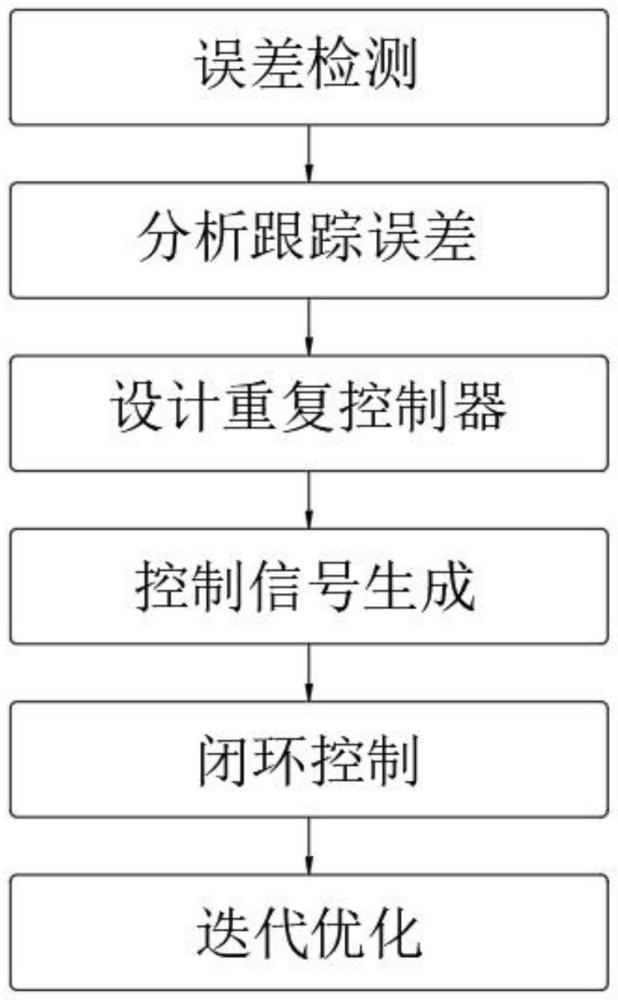
2、一种基于重复控制器的五轴机床旋转轴跟踪误差补偿方法，包括以下步骤：

3、s1：在五轴机床旋转轴上，监测实际位置与期望位置之间的跟踪误差，该跟踪误差作为控制单元的输入，控制单元接收跟踪误差输入后调整旋转轴的运动；

4、s2：通过对实际误差信号进行频谱分析，进行周期性误差分析；

5、s3：设计重复控制器，对特定频率的周期性误差进行补偿；

6、s4：基于重复控制器生成一个用于抵消周期性误差的信号，将该信号加入到重复控制器的控制信号中；

7、s5：将生成的控制信号与实际反馈信号结合，形成闭环控制，以抵消周期性误差；

8、s6：迭代优化，重复控制器基于迭代优化机制，在运行时不断调整参数，以适应动态变化。

9、进一步的，所述s1具体包括在五轴机床的旋转轴上安装位置传感器，使用旋转编码器的角度传感器来测量旋转轴的实际位置，在数控程序中设定旋转轴的期望位置，将位置传感器与数控程序连接，实时监测位置传感器提供的旋转轴的实际位置信息，并计算实际位置与期望位置之间的误差，即为跟踪误差。

10、进一步的，所述s2中的频谱分析基于傅里叶变换，具体包括：

11、采集跟踪误差作为控制单元的输入，对跟踪误差信号进行时域分析，以查看信号的波形和趋势，通过傅里叶变换将信号分解成一系列频率分量，将傅里叶变换应用于时域信号，把信号转换为频域，根据傅里叶变换的结果，生成频谱图，分析频谱图中的主要频率成分，确定误差信号中的周期性特征，根据旋转轴周期性误差是否在稳定范围内，判断是否需要补偿。

12、进一步的，所述s3中的重复控制器基于五轴机床闭环控制系统，用于减小周期性输入误差r(z-1)对闭环控制系统误差e(z-1)的影响，r(z-1)与e(z-1)的关系式为：

13、

14、将代入关系式中得：

15、

16、其中nts为误差周期，ts为样本时间，使稳态误差减小到0，令e(jω)＝0；

17、

18、由上式可得，当频率ω为参考频率的n倍时，稳态误差降为0，当参考信号的周期为nt时，e(s)为0。

19、进一步的，所述s3中还包括采用最小增益原理进行稳定性分析，设跟踪误差方程为：

20、

21、基于跟踪误差方程以及最小增益原理，稳定性分析包括：

22、s31：若原闭环gpc(z-1)是稳定的，则1-gpc(z-1)也是稳定的；

23、s32：若r(z-1)和d(z-1)是谐波周期信号，则[r(z-1)-d(z-1)][1-gpc(z-1)](1-z-n)具有消除干扰和使误差收敛的能力，若d(z-1)不是周期性的，d(z-1)不是谐波频率，则不能有效地消除d(z-1)，并会受到高频干扰而降低稳定性；

24、s33：为了验证稳定性，误差的最后一项1/(1-z-n[1-gpc(z-1])也需稳定。

25、进一步的，所述最小增益原理基于奈奎斯特准则，其稳定状态表示为：

26、

27、其中，p(ωt)和θ分别为gpc(z-1)的幅值和相位，则稳定条件为：

28、0≤p(ωt)＜2cosθ(ωt)；因此，θ的稳定范围在±90°之间，幅值的极限是2cosθ(ωt)。

29、进一步的，所述s5中的闭环控制包括通过曲线拟合方法求出线性传递函数，传递函数gr(z-1)表示为：

30、

31、则跟踪误差方程更新为：

32、

33、其中，q(z,z-1)是一个零相位低通滤波器，其低频增益≤1，用于增强抑制高频干扰的鲁棒性，因此，[r(z-1)-d(z-1)][1-gp(z-1)](1-q(z,z-1)z-n)将趋于稳定；

34、令gp(z-1)＝p(ωt)ejθ(ωt)，其中p(ωt)和θ分别是gp(z-1)的幅值和相位，则其中，f(ωt)和φ分别是gf(z-1)的幅值和相位，得到q(z,z-1)＝q(ωt)ej0＝q(ωt)，其中q(ωt)是q(z,z-1)的幅值，则稳定条件为：

35、

36、若p(ωt)稳定，通过调节kr、f(ωt)和来改变稳定范围，在任何相位都是稳定的，可得：

37、

38、本发明的有益效果：

39、本发明，基于重复控制器的五轴机床旋转轴跟踪误差补偿方法，原型重复控制器通过迭代优化的方式，有效地抑制了周期性输入引起的跟踪误差。

40、本发明，重复控制器相对于pid控制器更具适应性，能够在复杂系统中提供更为稳健的性能，重复控制器对于非线性系统具有较好的适应性，它在非线性系统中的性能通常比pid控制器更为稳健。

41、本发明，原型重复控制器还具有自适应调整的能力，能够根据实时的系统动力学变化进行参数调整。这种自适应性使得原型重复控制器能够更好地适应非线性和时变系统的变化，提高鲁棒性。