一种非最小相位高超声速飞行器的最优容错制导与控制一体化设计方法

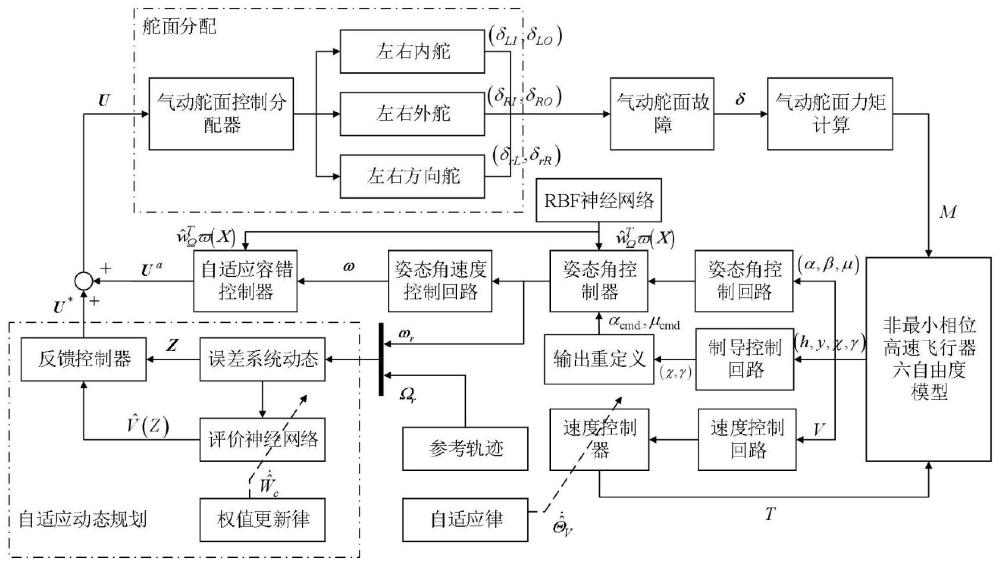
本发明涉及一种非最小相位高超声速飞行器的最优容错制导与控制一体化设计方法，属于自动控制。

背景技术：

1、作为一种新型快速、大空域、快速响应的空天飞行器，高超声速飞行器的动力学模型具有强耦合性，包括气动耦合、运动耦合、惯性和操纵耦合等，在大攻角飞行时尤为显著，这些耦合作用会导致飞行器运动学模型出现非线性和非最小相位特性。气动舵面是调节飞行器姿态和升力的关键部件，但其运动会对升力产生耦合影响，导致系统出现负超调现象。造成这种现象的主要原因是：在升力模型中存在气动舵面耦合项，从而使得系统的输入信号提前出现在输出信号低阶导数中，降低了系统的相对阶，导致不稳定内部动态的出现。因此，高超声速飞行器的纵向动态模型就是典型的非线性非最小相位系统。与最小相位系统相比，非最小相位系统的控制和输出跟踪更加复杂，需要在实现系统输出跟踪的同时确保内部状态的稳定，否则闭环系统将发散。对于非最小相位高超声速飞行器的输出跟踪控制问题，传统的非线性控制理论和输出跟踪控制方法不再适用。为了克服这些挑战，需要探索新的控制方法和技术稳定内部动态，以确保高超声速飞行器的安全运行。此外，高超声速飞行器的飞行环境恶劣、飞行条件变化大以及故障和损伤，这都会导致飞行器发生结构突变。因此飞行器控制系统的设计必须考虑飞行过程中可能发生的气动舵面故障的影响，以实现更高的安全性和可靠性。

2、目前针对高超声速飞行器的制导控制一体化设计已有一些研究成果。唐建等人提出了一种结合级联控制方法和控制障碍函数的新型三维制导控制一体化算法，在满足高超声速飞行器上升段过程约束的同时，实现飞行器的三维跟踪控制(考虑约束的高超声速飞行器制导与控制一体化设计.宇航学报,2022,43(05):649-664.)。但是该文献忽略了高超声速飞行器许多耦合，没有考虑飞行器的非最小相位特性。wang等人一种基于扩展回路backstepping方法的自适应容错制导与控制一体化策略，实现了对高度、速度和横向位移的近似跟踪(integrated design of adaptive fault-tolerant control for non-minimum phase hypersonic flight vehicle system with input saturation andstate constraints.proceedings ofthe institution ofmechanical engineers,partg:journal ofaerospace engineering,2022,236(11):2281-2301.)。但是该文献将气动舵面和气动力之间的所有耦合假设成系统不确定性项，仅仅能用于弱非最小相位系统的控制。此外，尽管该文献中已经研究了自适应容错问题，但该方法并未考虑高超声速飞行器的最优制导控制性能。

技术实现思路

1、发明目的：针对背景技术中指出的问题，本发明提供一种非最小相位高超声速飞行器最优容错制导与控制一体化设计方法，通过输出重定义、backstepping方法设计的制导控制信号，使得非最小相位高超声速飞行器在气动舵面故障下的有界稳定。随后，基于自适应动态规划技术设计的补偿控制信号用于在气动舵面故障情况下提供补充调整，以提高跟踪性能和容错能力。

2、技术方案：本发明公开了一种非最小相位高超声速飞行器的最优容错制导与控制一体化设计方法，包括如下步骤：

3、步骤1：建立非最小相位高超声速飞行器六自由度模型；

4、步骤2：建立气动舵面的故障模型，并引入状态约束函数；

5、步骤3：基于步骤1建立的高超声速飞行器六自由度模型，通过分析零动态的行为来推断其的内部动态特性；

6、步骤4：将步骤1建立的高超声速飞行器六自由度模型转换为制导与姿态子系统和速度子系统；

7、步骤5：针对步骤4转换之后的系统，结合步骤2建立的气动舵面故障模型和状态约束函数，设计速度子系统控制器，基于输出重定义设计制导子系统制导律，初步设计姿态子系统控制器及其反馈控制器和最优补偿控制器，进一步确定反馈虚拟控制器，根据气动舵面故障设计故障补偿控制器，基于设计的反馈控制器和故障补偿控制器实现高超声速飞行器在故障下的有界稳定；

8、步骤6：在姿态子系统引入最优控制性能指标，通过自适应动态规划迭代求解方法设计最优补偿控制器，使得高超声速飞行器控制系统闭环信号快速稳定，确保其在气动舵面故障和外部干扰情况下的飞行安全。

9、进一步地，所述步骤1高超声速飞行器六自由度模型为：

10、

11、

12、

13、

14、其中，x、y、h、v、χ、γ、α、β、μ、p、q、r为飞行器系统状态，分别表示前向位置、侧向位置、高度、速度、航向角、航迹角、攻角、侧滑角、倾侧角、滚转角速率、俯仰角速率、偏航角速率；m、g、t分别表示飞行器的质量、重力常数、发动机推力；ixx、iyy、izz为转动惯量；l、d、y分别为升力、阻力、侧力；mxx、myy、mzz为控制力矩在机体轴系三个方向的分量；力和力矩的表达式为：

15、

16、

17、其中，

18、

19、

20、式中，δ＝[δli δlo δri δro δrl δrr]t为六个舵面偏转量矩阵，δli为左内侧升降舵，δri为右内侧升降舵，δlo为左外侧升降舵，δro为右外侧升降舵，δrl为左方向舵，δrr为右方向舵；s为参考面积，为动压，ρ为大气密度，b为翼展弦长，c为平均气动弦长。

21、进一步地，所述步骤2气动舵面的故障模型为：

22、

23、式中，δc表述控制输入信号，σ＝diag(σ1 σ2 … σ6)表示六个气动舵面的舵效损失，表示舵面的卡死位置；σi∈[0,1]，τi＝{0,1}i＝1,2,…,6，气动舵面的所有工作状态为：

24、4)当0＜σi＜1且τi＝1时，δi(t)＝(1-σi)δci(t)，表示气动舵面发生部分失效故障；

25、5)当σi＝1且τi＝1时，表示气动舵面发生卡死故障；

26、6)当σi＝0且τi＝0时，δi(t)＝δci(t)，表示对应气动舵面正常工作，没有故障发生；

27、选择状态约束函数：

28、

29、其中，log(·)为自然对数函数，kb＞0为高超声速飞行器姿态误差z受约束的界，即|z|≤kb。

30、进一步地，所述步骤3内部动态的稳定性分析：系统输出向量选择为y＝[h,y,v]t，输入为超燃冲压发动机推力t和气动舵面的舵偏角向量δ，基于反馈线性化方法，对系统输出向量y连续求导，可得：

31、

32、

33、

34、

35、

36、对于输出向量y＝[h,y,v]t，相对阶向量为[2,2,1]，系统的相对阶为r＝2+2+1＝5，则系统存在6阶的内部动态η＝[α,β,μ,p,q,r]t：

37、

38、

39、

40、

41、

42、

43、该内部动态为一个6阶非线性系统，通过分析其零动态在平衡点[α,β,μ,p,q,r]＝[α*,0,0,0,0,0]处的局部稳定性来判断内部动态的稳定性。

44、进一步地，所述步骤4转换获得的制导与姿态子系统和速度子系统为：

45、速度子系统为：

46、

47、其中，推力t为该子系统的控制输入；

48、制导与姿态子系统为：

49、

50、

51、

52、其中，和为跟踪误差，χr和γr为期望值，ω＝[α,β,μ]t，ω＝[p,q,r]t，δfω为耦合项，制导与姿态子系统其余非线性函数如下：

53、

54、

55、

56、

57、

58、m＝a+bδ,

59、

60、进一步地，所述步骤5包括如下子步骤：

61、步骤51：速度子系统控制器设计：设计辅助动态系统处理推力饱和问题，定义速度跟踪误差为表示为辅助系统的状态，控制器t设计为：

62、

63、式中，kv表示速度跟踪误差的界，γv为待设计的正常数，为参数θv的估计值，估计误差定义为其更新律为：

64、

65、式中，为正常数；

66、步骤52：基于输出重定义的制导子系统制导律设计，将系统输出重新定义为ω，与之对应的内部动态为：

67、

68、式中，

69、

70、为了消除系统控制输入对内部动态的直接影响，基于lie导数的定义和微分同胚变换，定义坐标变换：

71、

72、式中，

73、

74、定义增广向量和其中，和的动态如下：

75、

76、采用小增益控制理论，给出如下的坐标变换：

77、

78、式中，ki1∈(0,1](i＝γ,χ)为待设计的正常数，为使内部动态和沿着期望输出轨迹局部渐近稳定，设计参考指令为：

79、

80、步骤53：姿态子系统控制器设计为u＝ua+u*，其中，u*为最优补偿控制器，反馈控制器反馈虚拟控制律设计为：

81、

82、式中，是待设计的对角正定矩阵；

83、设计反馈虚拟控制器ma为：

84、

85、式中，是待设计的对角正定矩阵；

86、步骤54：控制分配与容错策略设计，为了补偿未知的气动舵面故障，设计故障补偿控制器如下：

87、

88、式中，和分别代表k1和k2的估计值，且其自适应更新律设计如下：

89、

90、

91、式中，γk1和γk2均为待设计的对称正定矩阵；

92、步骤55：基于反馈控制器和容错策略设计，实现高超声速飞行器在故障下的有界稳定：

93、

94、其中，z＝[zt,ωt]t，

95、进一步地，所述步骤6包括如下子步骤：

96、步骤61：将高超声速飞行器姿态子系统的跟踪误差和改写为优化仿射非线性形式：

97、

98、其中，u*为最优补偿控制器；

99、步骤62：设计性能指标函数，并通过哈密顿函数优化该性能指标函数，通过最优容许控制得到最优控制策略u*，所述性能指标函数为：

100、

101、式中，q(z)表示半正定惩罚函数，r是对称正定矩阵；所定义的哈密顿函数为

102、

103、其中，表示v(z)对z的偏导数，

104、所述最优补偿控制器u*为：

105、

106、步骤63：基于自适应动态规划迭代求解方法，构建了一个神经网络在线近似最优代价函数vc*(z)，将神经网络的估计器进行梯度信息化，从而获得最优控制策略，神经网络估计器为：

107、vc*(z)＝wctσ(z)+εc(z)

108、式中，wc∈rl代表理想权值向量，σ(z)∈rl是评价网络的激活函数，εc(z)是评价网络的近似误差，存在一个正常数满足

109、评价网络的真实输出为将神经网络的估计器进行梯度信息化最优控制策略为：

110、

111、结合最优控制策略构成如下的哈密顿函数误差：

112、

113、步骤64：定义如下二次型目标函数：

114、

115、基于梯度下降法，设计评价网络权值更新律：

116、

117、其中，αc＞0表示评价网络学习率，ms＝1+φtφ，f1和f2是需要设计的相应维数的调节参数，

118、

119、本发明采用以上技术方案与现有技术相比，具有以下技术效果：

120、1、本发明采用输出重定义和backstepping方法提出了一个新的自适应容错制导与控制一体化策略，为复杂的强非线性、强非最小相位系统的近似跟踪控制提供了新思路。

121、2、本发明采用基于自适应动态技术的最优制导控制策略作为补偿控制器，从而改善了系统的瞬态性能，并增强了控制器的容错能力。此外，所设计的容错制导控制方法还考虑了状态约束，确保系统状态保持在一定范围内。