一种基于时间圆整策略的拐角平滑速度规划方法

本发明涉及机器人轨迹速度规划插补领域，尤其涉及一种基于时间圆整策略的拐角平滑速度规划方法。

背景技术：

1、在机器人控制中，为避免各轴产生冲击、震荡等，以保证运动部件的平稳运动，需要进行加减速控制。而且，目前的控制系统大都基于位置驱动的离散控制，数据下发周期即为插补周期，均为一固定时间周期。理论上总时间应为插补周期的整数倍，但是保证总时间是插补周期的整数倍且运动学参数不超限，难以实现。

2、公告号为cn107765639b的中国发明专利公开了一种s曲线加减速的圆整误差补偿方法，其仅列举了单条直线的速度规划，并不适用连续多段直线的圆整。因此，需要一种可以进行在线求解且能保证时间圆整的速度规划方法，以有效改善加工的振动。

技术实现思路

1、发明目的：提出一种基于时间圆整策略的拐角平滑速度规划方法，采用单段插补总时间圆整策略和s型速度曲线，旨在消除因圆整误差而引起的速度波动问题。

2、为达到上述目的，本发明的第一个方面，提出一种基于时间圆整策略的拐角平滑速度规划方法，包括如下步骤：

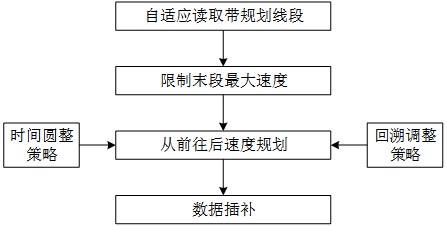
3、步骤一，自适应读取待速度规划线段，构建拐角曲线计算约束下的拐角速度；

4、步骤二，限制速度规划末段的最大速度；

5、步骤三，从前往后依次速度规划所有线段的速度并进行时间圆整；

6、步骤四，将速度规划好的数据进行插补运算。

7、在第一方面进一步的实施例中，步骤一中的自适应读取待速度规划线段有两个判别条件。每次取相邻的两条线进行判断，其一：已读取的总点数大于某一个固定值；其二：两条相邻线段的夹角小于90°；满足其中一个条件即停止数据读取。

8、在第一方面进一步的实施例中，步骤二中的限制速度规划末端的最大速度主要是避免后续的时间圆整带来的速度变化对前面已速度规划速度产生影响。末段速度主要来自三个速度约束，一是最后一个拐角速度；二是最大进给速度的k（）倍，三是前瞻末端点到拐角中点距离的一半所能加速的最大可达速度，取三者中的最小值。

9、在第一方面进一步的实施例中，前瞻末端点到拐角中点距离的一半所能加速的最大可达速度计算如下：假设最大可达速度能过达到最大进给速度，计算所需距离与实际距离的关系，若所需距离小于实际距离则可以达到最大进给速度，反之达不到最大进给速度；其次，假设存在匀加速段区域，基于七段式s型速度曲线计算纯加速的距离，若小于实际距离，则存在匀加速段，并基于运动关系列方程，通过一元二次方程计算最大可达速度；最后，达不到最大加速度且不存在匀加速段，且初速度不等于0时，通过运动关系列一元三次方程，利用卡尔达诺公式进行求解，初速度等于0时则直接求解一元三次方程。

10、在第一方面进一步的实施例中，步骤三从前往后速度规划所有线段时是基于s型速度曲线。若一条直线上从前往后是加速，基于步骤二的方法计算可达速度，并利用时间圆整策略圆整时间至插补周期的整数倍并计算对应的加加速度；若是减速，也基于步骤二的方法计算逆向可达速度，并利用速度圆整策略圆整时间至插补周期的整数倍并计算对应的加加速度；判断计算所得的加加速度是否超限。

11、在第一方面进一步的实施例中，时间圆整策略是：利用已计算的各个阶段时间总和向上圆整，并将圆整所产生的时间误差按比例分配至各个阶段，利用路径长度不变，求得匀速段的速度。并利用加速、减速段的速度与加加速度的关系，计算修正后的加加速度。若加速或者减速阶段修正的加加速度超过限定的加加速度，则进行二次修正。

12、在第一方面进一步的实施例中，二次修正时，依据始末速度大小关系，进行速度运行阶段调整。若初速度小于末速度，则二次修正呈现纯加速或者加速与匀速结合；若初速度大于末速度，则二次修正呈现纯减速或者减速与匀速结合；若初速度等于末速度，则二次修正呈现匀速状态；并以最大加加速度重新进行计算各阶段的时间并向上圆整时间，并以路径长度不变为条件，重新修正匀速段速度以及加速/减速的加加速度。

13、在第一方面进一步的实施例中，每条直线经时间圆整后得到的加加速度若依旧超限，需要结合前瞻速度规划方法进行消除。处于非回溯状态时加加速度超限，若当前线段是加速状态，则更新终点速度，重新调整当前线段；若当前线段时减速状态时，则更新起点速度，重新调整当前线段并回溯调整。处于回溯状态时加加速度超限，若当前线段是加速状态，则更新终点速度，并将前瞻段调整至当前段，重新调整当前段并往后圆整；若当前线段是减速状态，则更新起点速度，并将前瞻段调整至当前段的前一段，并重新往后圆整。

14、在第一方面进一步的实施例中，减速时，时间圆整后的初速度不等于拐角速度，则需要进行反向回溯调整。回溯调整时遇到正向加速时，且正向加速重新圆整的末速度等于拐角速度，则停止回溯继续前向调整速度；否则，进行回溯方向调整。

15、在第一方面进一步的实施例中，回溯时不满足加速段退出条件时，需要进行回溯方向调整。若加速段的初始速度大于后一条减速线段的末速度，则调整减速段的初始速度等于加速段的初始速度，重新圆整并继续往前回溯调整；若加速段的初始速度小于后一条减速线段的末速度，则调整加速段的末速度等于减速段的末速度，并调整回溯的方向向后进行调整，直至满足退出条件。

16、作为本发明的第二个方面，提出一种电子设备，该设备包括处理器以及存储有计算机程序指令的存储器；所述处理器执行所述计算机程序指令时实现如第一方面及其进一步的实施例所公开的基于时间圆整策略的拐角平滑速度规划方法。

17、作为本发明的第三个方面，提出一种计算机可读存储介质，存储介质中存储有至少一个可执行指令，所述可执行指令在电子设备上运行时，使得电子设备执行如第一方面及其进一步的实施例所公开的基于时间圆整策略的拐角平滑速度规划方法。

18、与现有技术相比，本发明具有如下的突出的实质性特点和显著性的技术进步：

19、1、本方法提出的圆整策略，可以进行在线求解并且保证所有的运动学参数均不超限，可以方便的集成到实时控制系统，从而实现在线速度规划。

20、2、本方法基于单段插补总时间的圆整策略，最低限度的降低补偿时间，提高了插补效率。而且，所有计算均有解析解，无需数值迭代求解。

21、3、本方法采用自适应读取待速度规划点位，在满足速度规划的同时避免一次处理较多点位而带来的内存空间占用大的问题。

技术特征：

1.一种基于时间圆整策略的拐角平滑速度规划方法，其特征在于，包括如下步骤：

2.根据权利要求1所述的基于时间圆整策略的拐角平滑速度规划方法，其特征在于，步骤一中所述读取待执行速度规划的线段有两个判别条件，每次取相邻的两条线进行判断；

3.根据权利要求1所述的基于时间圆整策略的拐角平滑速度规划方法，其特征在于，步骤二中所述限制速度规划末段的最大速度，包括三个速度约束，取三个速度约束中的最小值作为限制速度规划末段的最大速度；

4.根据权利要求3所述的基于时间圆整策略的拐角平滑速度规划方法，其特征在于，约束三中，所述前瞻末端点到最后一个拐角中点距离的一半所能加速的最大可达速度的计算方式如下：

5.根据权利要求4所述的基于时间圆整策略的拐角平滑速度规划方法，其特征在于，步骤三中，所述从前往后依次对所有线段执行速度规划的过程基于s型速度曲线；

6.根据权利要求5所述的基于时间圆整策略的拐角平滑速度规划方法，其特征在于，所述时间圆整策略包括：

7.根据权利要求6所述的基于时间圆整策略的拐角平滑速度规划方法，其特征在于，二次修正时，依据始末速度大小关系，进行运行阶段调整：

8.根据权利要求7所述的基于时间圆整策略的拐角平滑速度规划方法，其特征在于，每条直线经时间圆整后得到的加加速度若依旧超限，结合前瞻速度规划方法进行消除：

9.根据权利要求8所述的基于时间圆整策略的拐角平滑速度规划方法，其特征在于，减速时，时间圆整后的初速度不等于拐角速度，则进行反向回溯调整；回溯调整时遇到正向加速时，且正向加速重新圆整的末速度等于拐角速度，则停止回溯并继续前向调整速度；否则，进行回溯方向调整。

10.根据权利要求9所述的基于时间圆整策略的拐角平滑速度规划方法，其特征在于，回溯时不满足加速段退出条件时，进行回溯方向调整：

技术总结本发明提供了一种基于时间圆整策略的拐角平滑速度规划方法，涉及机器人轨迹速度规划插补领域。首先，通过自适应策略读取待速度规划线段，构建拐角曲线并计算约束下的拐角速度；其次，限制速度规划末端的最大速度避免下一次速度规划对前一次速度规划造成影响；然后从前往后速度规划所有线段，并在其中融合时间圆整策略，对于无法实现时间圆整的线段则结合回溯调整策略进行实现，从而实现对所有线段的时间圆整及速度规划；最后，建立局部拐角坐标系与全局坐标系的变换关系，并结合S型速度曲线进行插补。本方法采用自适应读取待速度规划点位，在满足速度规划的同时避免一次处理较多点位而带来的内存空间占用大的问题。技术研发人员：田威,李明宇,陈建云,廖文和,李鹏程,丁祎鑫,朱龙慧,康瑞浩受保护的技术使用者：南京航空航天大学技术研发日：技术公布日：2024/7/4