一种基于观测器级联的线性系统故障诊断方法

本发明涉及系统故障诊断，具体而言，为一种基于观测器级联的线性系统故障诊断方法。

背景技术：

1、自上世纪40年代以来，自动控制技术已经广泛应用于机器人、化工、航空航天、核电站等实际工程领域，并且在二十一世纪新工业化浪潮下继续发挥举足轻重的作用。随着实际系统的规模和复杂性日益增长，控制系统的成本也呈指数级增长。由于大型生产系统自身结构的复杂性和长时间大功率，高负荷地连续工作，系统中的一些设备如传感器及执行器都会无可避免地随着时间出现老化，甚至可能演变成故障，而一旦发生故障，系统的控制性能就会出现下降，甚至稳定性也无法得到保证，最后导致巨大的财产损失和人员伤亡。

2、故障诊断一般统指故障检测、故障隔离和故障辨识，故障检测与隔离技术的目标是确定故障发生时间及故障发生的位置和种类，与之不同，故障估计技术寻求在线获取更具体的故障动态信息，如故障的大小和形状，一般通过设计观测器来对故障进行估计，主要有滑模观测器、自适应观测器、未知输入观测器等。文传博等针对存在干扰的系统，结合广义观测器和滑膜观测器设计故障估计方法，估计并重构系统故障。pfodgaard等采用未知输入观测器估计变流器中的故障，并将故障划分为执行器和传感器故障，实现风力发电机组的故障诊断，提高了运行可靠性。shao,h.等针对4.8mw的风力发电机组系统，建造了风力发电机组的时变模型，其中叶片浆距角、叶尖速比和转子速度变成了实时更新的调度参数，设计了一种增强的时变观测器来估计风力发电机组系统中的参数故障和执行器故障。gaoz等利用未知输入观测器将干扰解耦或抑制，从而同时估计出系统状态和故障，进行准确有效的故障诊断。

3、未知输入观测器方法是为了求解鲁棒故障检测问题，在实际工程中，存在着外部干扰和不确定性等等，而且对象的许多参数是时变的，因此，精确的数学模型很难得到。随后，人们在这个方向做了大量的工作。该方法是将系统模型的不确定性作为一种未知的输入来处理，并利用未知输入观测器得到未知输入解耦的状态估计，然后通过状态估计形成的残差对未知输入进行解耦。一般情况下，在数学模型精确的条件下，我们会考虑采用观测器的方法，未知输入观测器方法进行故障诊断就是利用观测器的输出和系统正常输出来形成残差，最后判断故障的情况。然而，当发生多故障时，故障之间会互相影响，且由于精确系统难以获得，实际工程中会产生许多不确定因素，在故障和不确定性因素的多方面干扰下，想要准确得到故障信息非常困难。

4、因此，推出一种基于观测器级联的线性系统故障诊断方法。

技术实现思路

1、本发明的目的在于提供一种基于观测器级联的线性系统故障诊断方法，旨在解决上述背景技术中，故障发生较多时彼此间相互影响和外部干扰因素影响，造成观测器难以获得准确系统故障信息的问题。

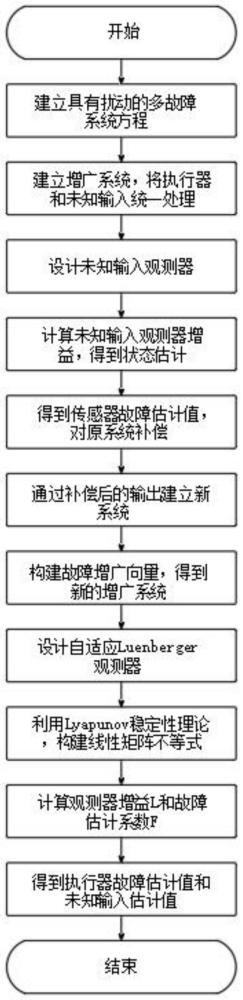
2、为实现上述目的，本发明提供如下技术方案：一种基于观测器级联的线性系统故障诊断方法，包括以下实施步骤：

3、s1：建立系统方程，利用增广方式得到增广系统，其中将执行器故障和未知输入共同看作新的未知输入；

4、s2：设计未知输入观测器，利用未知输入观测器特点将增广系统中的未知输入解耦；

5、s3：考虑未知输入观测器存在的充分必要条件；

6、s4：计算未知输入观测器增益r、t、k和h，得到状态估计，估计出传感器故障大小；

7、s5：将传感器故障估计值补偿到原系统中，得到新的补偿后系统；

8、s6：根据传感器补偿后的新输出，将原系统未知输入和执行器故障构成新的故障向量，得到又一新的增广系统；

9、s7：设计自适应luenberger观测器，构建误差动态方程和lyapunov函数；

10、s8：利用lyapunov稳定性理论得到线性矩阵不等式，通过线性矩阵不等式方法计算观测器增益l，求解故障估计系数f。

11、进一步地，所述s1中，系统方程为动力系统的状态空间方程，其公式如下：

12、

13、x(t)∈rn u(t)∈rm y(t)∈rp

14、其中， 是状态向量， 是控制输入向量， 是测量输fa(t)∈rq fs(t)∈rl d(t)∈rw

15、出向量， 是执行器故障， 是传感器故障， 是输入扰动，其中q+l+w＞p,q+w≤p；a、b、c、d、g和q分别具有适当的矩阵维数。

16、进一步地，所述s2中，设计未知输入观测器估计出系统传感器故障，令建立如下所示的增广系统：

17、

18、其中

19、进一步地，基于所述状态空间方程(2)式，设计如下形式的未知输入观测器：

20、

21、其中，令是式(3)系统中状态向量，

22、

23、是增广状态

24、k＝k1+k2

25、向量的估计，r、t、k和h是需要设计的观测器增益，且，使得状态估计误差则有：

26、

27、进一步地，所述公式(4)存在需考虑的条件包括：

28、

29、

30、

31、k2＝rh(8)，

32、那么状态误差就会变成：

33、

34、通过公式(9)可以得到_d已经被解耦了，求解公式(6)和设计系统矩阵r使观测器稳定，计算k1、k2和t。

35、进一步地，所述s3中，要使得未知输入观测器(3)式存在，需要满足的充分必要条件是：

36、(1)

37、(2)是可观测的，其中

38、依据lyapunov稳定性理论和求解得到的矩阵r、t、k和h使得未知输入观测器(3)式成立，得到状态估计且依据状态估计可得到：

39、

40、进一步地，得到所述公式(10)后，由此可得新系统：

41、

42、令建立如下所示的增广系统：

43、

44、进一步地，基于所述状态空间方程(12)式，设计如下形式的luenberger观测器：

45、

46、进一步地，将所述公式(12)系统中的视为新的执行器故障，当有执行器故障发生时，得到如下动态误差方程：

47、

48、根据动态误差方程式构造lyapunov，且设γ为自适应率：

49、得，

50、进一步地，利用所述lyapunov稳定性理论建立线性矩阵不等式，存在正定对称矩阵p，对称可逆矩阵h，以及y、f使得以下式子成立：

51、

52、

53、y＝pl(18)，

54、由线性矩阵不等式(15)使得状态误差和故障估计误差能一致最终有界，可得到正定对称矩阵p和y、h，通过式(18)可得到观测器式(13)中增益l，通过观测器式(13)中得到：

55、

56、由式(19)设定合适的自适应率γ，可以求得未知扰动和执行器故障的估计值，完成整个系统的故障估计。

57、与现有技术相比，本发明的有益效果如下：

58、本发明提出的一种基于观测器级联的线性系统故障诊断方法，通过未知输入观测器和自适应luenberger观测器级联的故障估计方法，使用两种观测器级联的形式在输出信息不足的情况下进行故障估计，估计执行器故障、传感器故障和未知扰动，并根据未知输入观测器的特点，将执行器故障以及未知输入解耦，得到传感器故障，对原系统补偿再设计自适应luenberger观测器，采用故障补偿的方式消除部分故障影响，然后利用线性矩阵不等式算法设计观测器增益，实现执行器故障和未知输入的鲁棒估计，有效避免了在故障和外界不确定性因素的多方面干扰下，观测器难以获得系统准确故障信息的问题，提高了观测器对系统故障信息检测准确性。