分数阶多Euler-Lagrange系统有限时间跟踪控制方法

本发明涉及分数阶多智能体系统的有限时间跟踪控制领域，具体涉及分数阶多euler-lagrange系统有限时间跟踪控制方法。

背景技术：

1、近年来，随着人工智能技术和分布式控制方式不断结合，机械臂凭借自身的独特优势得到了快速发展，并广泛应用于不同领域进行作业生产。在实际生产中，机械臂系统往往还会受到各种不确定的非线性因素影响，这对机械臂的控制提出了越来越高的要求。针对不同的生产作业要求，可以设计符合实际情况的机械臂外观和预定的运动轨迹，使其不仅能在有毒有害或者危险的环境下进行作业生产，从而保护工作人员的生命健康安全，而且还能代替人进行重复单一性的工作任务，实现自动操作运行，减轻人非必要的劳动量，能够大大提高作业生产效率。

2、然而，多euler-lagrange系统的跟踪控制问题是多智能体跟踪控制中重要的组成部分，因此受到国内外学者的广泛关注和研究。目前主要的研究方法有基于sm、基于pid、基于自适应、基于backstepping以及鲁棒等跟踪控制方法，因sm变结构具有响应速度快、强鲁棒性的优点，所以常采用sm控制来解决多euler-lagrange系统跟踪控制问题。在现有的文献中，研究了系统存在模型不确定性和外界干扰、考虑系统外部干扰和内部不确定性以及系统在含有障碍物等情况下多euler-lagrange系统的跟踪控制问题。

3、在选取sm控制时，需要考虑到如何避免出现奇异现象和抖振现象。在设计sm控制器时，常常会因为sm函数的不合理选用导致sm控制器趋于无穷大，从而出现奇异现象。对于此，需要选取一个ntsm函数来避免出现奇异现象；而基于ntsmc下设计的有限时间控制器能够避免出现抖振现象。

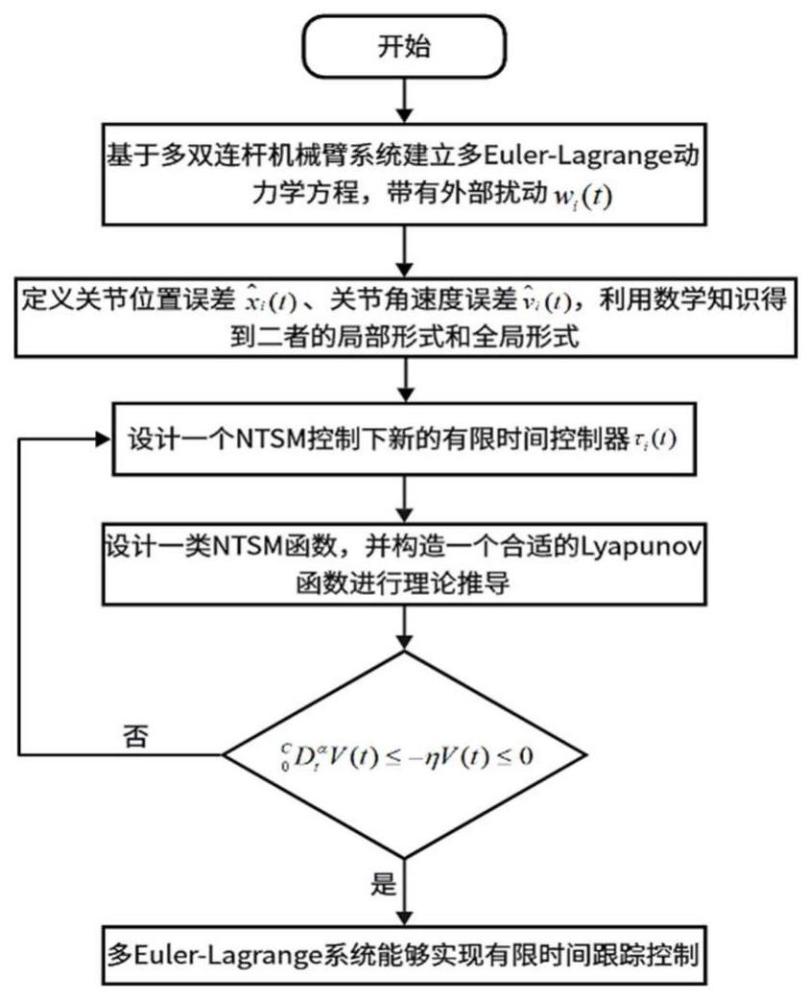
4、因此，本发明将基于多双连杆机械臂模型建立多euler-lagrange动力学方程(带有外部扰动wi(t))，定义关节位置误差关节速度误差引入caputo分数阶微积分的概念得到二者的分数阶局部形式，再借助kronecker积，将二者简化为全局形式；设计一个ntsm控制下新的有限时间控制器τi(t)，引用分数阶多euler-lagrange系统的lyapunov稳定性理论；设计一类ntsm函数，并构造一个合适的lyapunov函数，从理论角度证明分数阶多euler-lagrange系统状态在有限时间内收敛。

技术实现思路

1、发明目的：针对背景技术中指出选取sm控制时需要考虑的问题，本发明公开一种分数阶多euler-lagrange系统有限时间跟踪控制方法，设计一个ntsm控制下新的有限时间控制器，引用分数阶多euler-lagrange系统的lyapunov稳定性理论；设计一类ntsm函数，并构造一个合适的lyapunov函数，从理论角度证明分数阶多euler-lagrange系统状态在有限时间内收敛。

2、技术方案：本发明提供了本发明提供了一种分数阶多euler-lagrange系统有限时间跟踪控制方法，设计合适的非奇异终端滑模ntsm使得多euler-lagrange系统状态在有限时间内收敛，包括以下步骤：

3、步骤1：根据多双连杆机械臂系统模型建立多euler-lagrange动力学方程，动力学方程中包含外部扰动wi(t)，并给出多双连杆机械臂系统所满足的性质和假设；

4、步骤2：定义关节位置误差关节速度误差引入caputo分数阶微积分将改写为分数阶局部形式借助kronecker积，将改写为分数阶全局形式

5、步骤3：基于建立的多euler-lagrange动力学方程，设计一个非奇异终端滑模控制ntsmc下有效的有限时间控制器τi(t)；

6、步骤4：引用适合分数阶多euler-lagrange系统的lyapunov稳定性理论，以及定义有限时间达成分布式跟踪控制目标的条件；

7、步骤5：选取一类非奇异终端滑模ntsm函数，并构造一个合适的lyapunov函数，从理论角度证明分数阶多euler-lagrange系统状态在有限时间内收敛。

8、进一步地，所述步骤1中多euler-lagrange系统由n个双连杆机械臂组成，其第i个双连杆跟随机械臂的动力学方程如式(1)所示：

9、

10、其中，分别为第i个双连杆跟随机械臂的关节角速、关节角速度、关节角加速度，分别为第i个跟随机械臂的对称正定惯性矩阵、向心科里奥利矩阵、重力矢量，分别为第i个跟随机械臂的广义控制力矩、外部扰动；

11、多euler-lagrange系统满足以下性质和假设：

12、性质1：有界性，存在正常数k1、k2、k3，使得

13、

14、其中，in为n阶单位矩阵，i＝1,2,…,n；

15、性质2：反对称性，是反对称矩阵，对任意给定的向量有

16、

17、其中，i＝1,2,…,n；

18、假设1：多euler-lagrange系统中模型的不确定性和外部扰动wi(t)是有界的，即

19、‖m-1(q)wi(t)‖≤wsup  (4)

20、其中，wsup是已知的最小上确界，且wsup>0。

21、进一步地，所述步骤2中多euler-lagrange系统定义关节位置误差关节速度误差分别如式(5)、(6)所示：

22、

23、

24、其中，分别为领导者的关节角度、关节角速度；

25、借助caputo分数阶微积分概念，并结合式(1)可将式(5)、(6)改写为：

26、

27、

28、借助kronecker积，将式(7)、(8)分数阶局部形式改写为分数阶全局形式，分别如式(9)、(10)所示：

29、

30、

31、其中，各全局变量的具体定义如下：

32、

33、

34、m(q)＝diag{m1(q1),m2(q2),…,mn(qn)},

35、

36、

37、进一步地，所述步骤3中基于建立的多euler-lagrange动力学方程，设计一个ntsmc下有效的有限时间控制器τi(t)如式(11)所示：

38、

39、其中，τ(t)是τi(t)的全局形式，sign(s(t))是s(t)的符号函数，s(t)为ntsm函数，β＞0,η为非负数，p1、p2均为奇数，且满足p2＜p1＜2p2，具体定义如下：

40、

41、

42、其中，分别为领导者的关节角速度、关节角加速度；

43、为了简化证明过程，将(11)进一步改写为：

44、

45、其中，τ＝τ(t),s＝s(t)。

46、进一步地，所述步骤4中引用适合分数阶多euler-lagrange系统的lyapunov稳定性理论如式(13)-(14)所示：

47、令x(t)＝0是非自治分数阶系统

48、的平衡点，如果存在lyapunov函数v(t)和一个非负数η，满足下式：

49、

50、则称(13)是渐近稳定的；

51、定义有限时间达成分布式跟踪控制目标的条件如式(15)-(16)所示：

52、

53、

54、其中，qi(t)表示为第i个双连杆跟随机械臂的关节角速，为第i个双连杆跟随机械臂的关节角速度，q0(t)领导者的关节角度，为领导者的关节角速度，为了简化证明过程可以将qi(t)、q0(t)、简化为qi、q0、

55、进一步地，所述步骤5中选取的一类ntsm函数如式(17)所示：

56、

57、对于多euler-lagrange系统，且ntsm函数(17)满足：

58、s(t)＝0  (18)

59、则多euler-lagrange系统状态q,在有限时间内收敛；

60、构造的lyapunov函数如式(19)所示：

61、

62、有益效果：

63、本发明选取一个ntsm函数，并且基于ntsm函数下设计一个新的有限时间控制器，这样可以避免多双连杆机械臂系统出现奇异现象和抖振现象。首先基于多双连杆机械臂模型建立多euler-lagrange动力学方程(带有外部扰动wi(t))；接着定义关节位置误差关节速度误差引入caputo分数阶微积分的概念得到二者的分数阶局部形式，再借助kronecker积，将二者简化为分数阶全局形式；然后设计一个ntsm控制下新的有限时间控制器τi(t)，引用分数阶多euler-lagrange系统的lyapunov稳定性理论；最后设计一类ntsm函数，并构造一个合适的lyapunov函数证明出分数阶多euler-lagrange系统状态在有限时间内收敛，即原ntsmc下具有外部扰动的分数阶多euler-lagrange系统能够实现有限时间跟踪控制。