应用于多目标柔性车间调度的双层动态元启发式方法

本发明涉及柔性作业车间调度，具体为应用于多目标柔性车间调度的双层动态元启发式方法。

背景技术：

1、随着全球经济高速发展，调度在生产系统的决策和智能制造的资源分配中扮演着至关重要的角色。柔性作业车间调度问题作为调度领域的经典问题，受到广泛的研究关注，并且和实际工业有着密切的联系[1]。例如汽车行业中的装配线调度、内饰和电子系统装配、零部件供应调度。与作业车间调度(jsp)相比，柔性作业车间调度(fjsp)在考虑工件所有工序加工顺序的同时，还要考虑每道工序的机器分配问题，是更复杂的np-hard问题[2]。因此，深入研究fjsp不仅具有理论意义，而且具有一定的应用价值。

2、目前解决fjsp的算法，主要分为精确式算法、启发式算法、元启发式算法。其中精确式算法包括分支定界法和动态规划等方法[3]。对于小规模数据问题，精确式算法理论上来说可以得到最优解。但是由于其时间和空间复杂度较高，往往难以应用于实际问题。启发式算法是通过对过去经验的归纳推理以及实验分析来解决问题的方法，即借助于某种直观判断或试探的方法，以求得问题的次优解。例如spt规则，即加工时间最短的工件优先加工[4]。虽然启发式算法可以很快求得问题的解，但是很难保证算法的收敛性。元启发式算法由于其原理简单，对初始值不敏感，易于实现，被广泛地应用于处理非线性优化问题。此外，元启发式算法不依赖于目标函数的梯度，这也使得解决方案的适用性更有说服力。

3、考虑到元启发式算法的优点，近些年越来越多的学者将元启发式算法应用于fjsp的求解中。caldeira等人[5]提出一种基于pareto的jaya算法去解决fjsp，并增加局部搜索和变异算子，使得算法性能得到了极大的改善。zhang等人[6]针对不同性能指标下柔性作业车间调度问题进行了研究，提出了一种具有双层子代产生模式的改进遗传算法。karthikeya等[7]提出了一种混合离散萤火虫算法求解有限资源约束下的多目标柔性作业车间调度问题。rylan等人[8]设计了一个以完工时间和能源总消耗为目标的柔性作业车间调度问题，提出了一种有效的回溯算法(backtracking search algorithm)对其进行求解。并通过实验验证了方法的有效性。dileeplal等人[9]开发了一种基于置换编码方案的多目标遗传算法，并设计了保留优先权的进化算子来解决多目标装备作业车间调度。

4、为了在生产和制造领域推动可持续发展和环保，绿色调度成为了企业和组织在追求盈利的同时，充分考虑环境和社会责任的关键策略之一。越来越多的学者开始研究绿色车间调度的方法和技术，以寻求在生产过程中实现资源优化、能源效率和环境保护的最佳平衡点。gong等人[10]关注了工人灵活性和绿色生产相关因素，提出了一个多目标柔性车间调度问题。在研究中，构建了一个非线性整数规划模型，并引入了一种新的非支配集合适应性排名算法来解决这个问题。li等人[11]提出了具有装置时间和运输时间等约束的多目标绿色调度问题，并使用改进的jaya算法进行解决。wu等人[12]开发了一种混合鸽子优化和模拟退火算法来解决具有劣化效应的绿色柔性车间调度问题。lei等[13]设计了一种混合蛙跳算法对优化负荷平衡和总能耗的fjsp进行了研究，分析并验证了这两个目标的冲突性。mokhtari等人[14]建立了以完工时间、设备利用率和总能耗为目标的多目标优化模型，提出了用遗传算法与模拟退火算法相结合的混合算法进行求解。

5、上述文献所呈现的研究成果无疑具有其重要性，然而，其中存在两个明显的不足。从算法的角度来看，这些研究中提出的改进策略通常局限于特定的算法或问题领域。因此，这些策略在其原本设计的领域内可能非常有效，但将相同的改进策略迁移到其他算法或问题上就变得相当具有挑战性。因为不同算法和问题可能涉及不同的数据结构、约束条件和优化目标。从fjsp的角度进行分析，调度最优解不仅仅取决于工序的加工顺序，也要考虑到机器的分配。目前大多数元启发式算法在解决fjsp的做法分为三类。第一类，将工序和机器进行统一编码，然后通过特定的元启发式算法进行搜索。第二类，将工序单独编码，不同工序随机选择机器加工。第三类，将工序单独编码，引入机器分配规则，并对这些规则赋予固定权重。但是这三类解决方案具有不同的缺点。第一种解决方案的缺点：将工序和机器进行统一编码，会导致问题的维度增加，算法的探索能力会变弱。第二种解决方案的缺点：由于机器是随机选择的，很难保证算法的收敛性。第三种解决方案的缺点：虽然引入了机器分配规则，增加了算法选择的多样性，然而优化问题是动态变化的，固定的机器分配规则权重很容易使得算法陷入局部最优解。

6、因此需要对以上问题提出一种新的解决方案。

技术实现思路

1、本发明的目的在于提供应用于多目标柔性车间调度的双层动态元启发式方法，以解决背景技术中提出的问题。

2、为实现上述目的，本发明提供如下技术方案：应用于多目标柔性车间调度的双层动态元启发式方法，至少包括以下步骤：

3、s1：模型建立，用于优化两个主要目标函数，所述两个主要目标函数包括最小化最大完工时间和最低总能源消耗，其中，最大完工时间表示所有工件完成加工的时间中的最大值，即最后一个工件的完成时间，总能源消耗包括车间的固定能源消耗和机器的加工能源消耗；

4、s2：搭建双层动态元启发式算法框架，所述搭建双层动态元启发式算法框架至少包括工序编码、机器指派规则、工序解码、双层动态元启发式算法、案例研究、多目标处理方法和邻域搜索；

5、s3：实验分析。

6、优选的，所述模型建立如下：

7、目标函数涵盖公式1和公式2；

8、所述公式1为：

9、min f1＝max1≤i≤n(ci)

10、所述公式2为：

11、

12、其中，f1代表最大完工时间，f2代表总能耗；

13、所述约束条件包括公式3、公式4、公式5、公式6、公式7、公式8和公式9；

14、所述公式3为：

15、sij+xijk×tijk≤cij

16、所述公式4为：

17、cij≤si(j+1)

18、所述公式5为：

19、

20、所述公式6为：

21、sij+tijk≤slh+l(1-yijlhk)

22、所述公式7为：

23、cij≤si(j+1)+l(1-yijl(h+1)k)

24、所述公式8为：

25、

26、所述公式9为：

27、sij≥0,cij≥0

28、所述公式3和公式4代表每一个工件的工序具有先后顺序，所述公式5代表每一个工件的完工时间等于该工件最后一道工序的结束时间，所述公式6和公式7代表同一时刻同一台机器只能加工一道工序，所述公式8代表同一时刻同一道工序只能且仅能被一台机器加工所述，公式9表各个变量必须是正数；

29、所述公式1、公式2、公式3、公式4、公式5、公式6、公式7、公式8和公式9中的符号意义如下：

30、n为工件总数；m为机器总数；p为工序总数；k为机器序号；i,l和j,h为工件序号；

31、

32、

33、oij为工件i的第j道工序；oijk为工件i的第j道工序在机器k上加工；pi为工件i的工序总数；mij为工件i的第j道工序的可选加工机器数；l为一个足够大的正数；tijk为工件i的第j道工序在机器k上的加工时间；waijk为工件i的第j道工序在机器k上单位加工时间的能耗；wk为机器k在单位时间内的固定能耗；sij为工件i的第j道工序加工开始时间；cij为工件i的第j道工序加工结束时间；ci为工件i的完工时间。

34、优选的，所述工序编码采用升序排列规则编码；

35、所述升序排列规则编码的具体规则如下：

36、首先生成一组连续向量xi＝[xi1,xi2,…,xid]和工件编号向量j＝[j1,j2,…,jd]；

37、然后挑选出连续向量中最小的位置，并分配工序编号为1，再次挑选出连续向量中第二小的位置，分配工序编号为2；

38、类似的，依次将所有的连续向量转换为工序编号。

39、优选的，所述机器指派规则包括优先分配加工时间的最小的机器、优先选择当前负载量最小的机器和随机分配机器。

40、优选的，所述工序解码采用插入式贪婪解码算法，其算法步骤如下：

41、步骤1：计算工序的开工时间，每道工序的开工时间等于其工件前道工序和机器前道工序完工时间的最大值；

42、步骤2：查找此工序前面的可用机器空闲时间；

43、步骤3：在不推迟其他已安排工序开工时间的条件下，将其插入对应机器上最早可行的加工时刻。

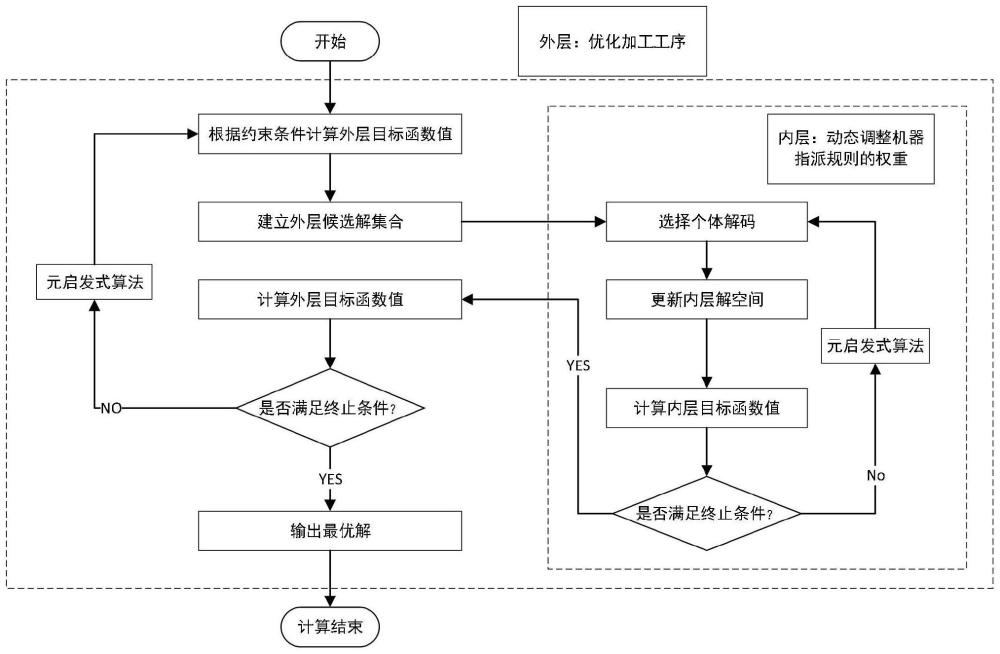
44、优选的，所述双层动态元启发式算法(bi-layer dynamic metaheuristicalgorithm,bldma)包括外层元启发式算法和内层元启发式算法；

45、所述外层元启发式算法和内层元启发式算法的搜索结构是相同的，但两者的编码不同；

46、所述外层元启发式算法中每个个体的维度是和工件总数及每个工序数相关；

47、所述内层元启发式算法中每个个体的维度是机器指派规则的数量；

48、由于机器指派规则有三个，即每个内层算法的个体维度为3；

49、每种机器指派规则的权重范围为(0，1)，并且三个权重的加和等于1；

50、基于此，增加归一化方法将每个权重映射在0-1之间，其数学表达式如下：

51、

52、其中q1,q2,q3分别代表机器指派三种规则的权重。

53、优选的，所述多目标处理方法选用帕累托方法，所述多目标处理方法具体方法如下：

54、步骤1：首先对种群中不同个体之间的支配关系进行判断；

55、步骤2：根据步骤1得到的结果，找到当前种群中的非支配最优解，构建paretofront，同时将pareto front中的个体的等级排名为1，并将其在种群中删除；

56、步骤3：将pareto front中的个体放到规模为k的外部档案集中，并从其中随机选择一个个体，引导下一次种群进化，如果外部档案集中的个体数量n大于k，则随机删除n-k个个体；

57、步骤4：判断是否满足终止条件，如果不满足，则更新种群，重复执行以上步骤。

58、优选的，所述邻域搜索至少包括以下步骤：

59、首先，找出分配加工工件数最多的机器；

60、其次，随机选择一个分配到该机器上的工件；

61、最后，将所选工件重新分配给加工时间较短的其他机器；

62、所述邻域搜索的伪代码如下所示：

63、mac_pin＝[]；

64、％count the frequency of each machine allocation

65、mac_pin＝tabulate(schedule(:,machine_column))；

66、％get the machine with the most job allocations

67、[mac_max_index]＝max(mac_pin)；

68、％get the schedule of the machine with the most job allocations

69、mac_max_schedule＝schedule(schedule(:,machine_column)＝＝mac_max_index,:)；

70、％randomly select a job

71、mac_max_temp＝randperm(size(mac_max_schedule,1))；

72、choose_mac_job＝mac_max_schedule(mac_max_temp(1),job_column)；

73、choose_mac_seq＝mac_max_schedule(mac_max_temp(1),operation_column)；

74、％check available machines for the current job and operation

75、choose_mac_pin＝mac_pin(mac{choose_mac_job,choose_mac_seq},:)；

76、％get the machine with the fewest job allocations

77、[～,temp_mac]＝min(choose_mac_pin)；

78、[～,ind]＝ismember(schedule,mac_max_schedule(mac_max_temp(1),:),'rows')；

79、％implement the transfer of the machine where the job is beingprocessed

80、schedule(find(ind,1),machine_column)＝choose_mac_pin(temp_mac,1)。

81、与现有技术相比，本发明的有益效果是：

82、本发明通过对"双层动态元启发式算法框架"的开发和应用，该框架由两个嵌套的元启发式算法层组成，分别为外层元启发式算法和内层元启发式算法，在解决优化问题时，这两层算法协同工作，以实现更好的决策效果；

83、首先，在本发明中，外层元启发式算法承担了首要决策的角色，负责确定工序的加工顺序，一旦外层算法确定了加工顺序，内层元启发式算法则发挥作用，根据外层已确定的工序加工顺序来调整机器指派规则的权重；

84、且上述这一协作机制是动态的，即在算法求解过程中随着问题的不同和外层元启发式算法的变化而调整；

85、这意味着算法能够根据问题的性质实时调整决策策略，以更好地适应不同场景，从而提高了寻找最优解的潜力。

86、这一算法框架的关键之处还在于，它并不依赖于特定算法的内部结构或工作原理，相反，它专注于优化问题的解决过程，并通过内外层元启发式算法的协同作用来动态调整决策策略；

87、这种设计使得框架可以灵活地嵌入到各种算法中，而不需要对这些算法进行根本性的修改，即使针对于不同的算法，本发明所提出的算法框架均有较好的适用性。