一种求解全局最优的组合式机器人接触式标定方法及系统

本发明涉及机器人接触式标定，尤其是指一种求解全局最优的组合式机器人接触式标定方法及系统。

背景技术：

1、壁板类部件广泛应用于航空航天结构件，通常用于各种承载应用。这些部件通常使用数控机床进行加工。为了提高表面质量和延长疲劳寿命，需要消除零件表面的刀痕。此外，在部件表面经常留有一定程度的残余毛刺和凸台，而去除这种毛刺所需的手工磨削是一个耗时的过程。

2、机器人可以夹持多种设备（测量工具，加工工具），同时也可与外部的标定测量设备通讯。通过标定、测量、加工一体化操作完成结构件的自动化匹配加工工作。为了高效率、高质量的完成壁板类零件去除凸台残余以及加工刀痕，由于机器人工作单元具有铣削和打磨的复合加工能力，因此可选择使用机器人工作单元完成上述功能。由于结构件种类多样，设计专用的装夹工装的成本很高，且需要频繁更换夹具，导致使用专用工装的方案效率低，自动化水平低。因此设计了机器人磨抛柔性工装，工装采用真空吸附与磁性固定相结合的方式，可以实现工件在工作台随意放置。

3、由于工件在工作台上可以任意位置放置，工件位置不确定，在进行加工前，需要对工件进行标定定位，确定工件坐标系，然后才能使用离线程序进行加工。要提高机器人加工精度，重点就集中于提高机器人加工系统坐标系标定精度。机器人加工系统坐标系标定主要是工具坐标系和工件坐标系的标定，其标定精度对后续的加工操作具有重要意义。

4、目前，除了视觉测量的方式外，还可以通过接触式红宝石测头标定来现机器人加工系统坐标系标定。用“球对球”法代替传统的点对点法对柔性固定探头架进行标定；然后，利用标定后的测头，精确寻找工具原点，对工具进行精确标定。

5、公开号为cn109848989a的专利中，公布了一种基于红宝石探针的机器人执行末端自动标定及检测方法。通过利用固定红宝石探针对工件表面轮廓进行触碰探寻标定，计算工件加工前后表面轮廓度，将计算结果输送至机器人控制器中，实现机器人末端工件表面轮廓度计算并显示。能够实现机器人执行末端自动标定并自动完成工件加工前后的表面轮廓度检测。

6、公开号为cn111941425a的专利中，公布了一种基于激光跟踪仪和双目相机的机器人铣削系统工件快速定位方法。基于激光跟踪仪和双目相机的机器人铣削系统工件快速定位方法。该方法能够将双目相机扫描得到的点云快速转换到工件坐标系下，通过点云处理，提取出工件坐标系下的特征点，然后基于这些特征点引导机器人移动到特征点位置处。这种方法不仅效率高，而且避免了人工示教的误差，提高了机器人铣削系统工件定位的精确度。

7、上述专利中，使用的激光跟踪仪和双目相机虽然能够满足自动化测量标定工件，但整体设备成本较高，难以实现低成本的广泛应用。此外，采用非线性最小二乘法优化tcp标定结果，易陷入局部最优情况，导致求解参数的结果不准确，影响最终标定质量。

技术实现思路

1、为此，本发明提供一种求解全局最优的组合式机器人接触式标定方法及系统，通过相互迭代的过程获得全局最优解，保证算法的效率，同时最大限度地提高了全局最优求解能力。对于提高机器人加工系统坐标系标定精度，其标定精度对后续的加工操作具有重要意义。

2、为解决上述技术问题，本发明提供一种求解全局最优的组合式机器人接触式标定方法，包括：

3、获取在机器人的红宝石测头与标准球接触时，机器人手腕末端的坐标系到机器人基坐标系的齐次变换矩阵；

4、基于所述红宝石测头的坐标系原点和所述标准球的球心分别在机器人基坐标系下的位置，建立标定模型；

5、基于所述标定模型，根据非线性最小二乘优化方法，建立目标函数；

6、基于所述目标函数，利用l-m方法与direct方法进行循环迭代计算，得到所述目标函数的全局最优解，包括：

7、设置l-m方法的初始参数并迭代计算，响应于所述目标函数通过l-m方法迭代计算收敛至局部最小值，将对应所述局部最小值的局部最小值点作为direct方法的初始参数；

8、响应于所述目标函数通过direct方法迭代计算得到的函数值小于所述局部最小值，更新l-m方法的初始参数，将对应所述函数值的点作为l-m方法的新的初始参数，再次迭代计算；

9、重复循环迭代计算步骤，直至通过l-m方法得到所述目标函数的全局最优解；

10、基于所述全局最优解，得到红宝石测头的坐标系原点位置参数。

11、在本发明的一种实施方式中，获取在机器人的红宝石测头与标准球接触时，机器人手腕末端的坐标系到机器人基坐标系的齐次变换矩阵，包括：

12、将标准球安装在磁性底座上，并通过磁铁将其吸附在机器人可达范围内的固定支架上；

13、机器人通过不同位置和姿态向标准球进行运动；

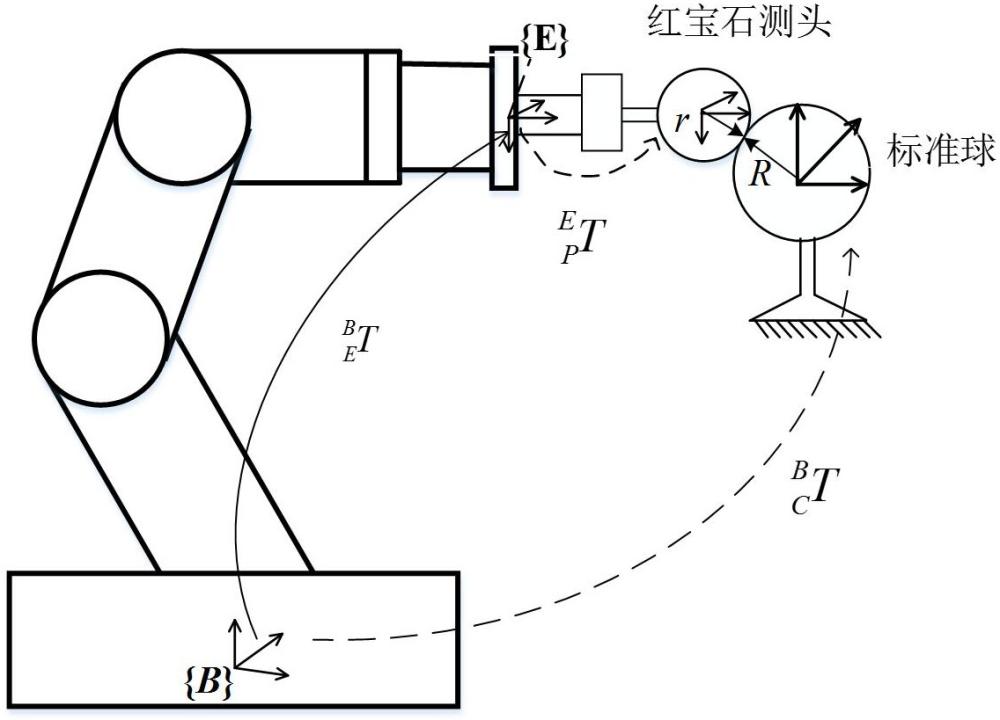
14、通过机器人控制器获取红宝石测头与标准球每次接触时，机器人手腕末端tool0的坐标系{e}到机器人基坐标系{b}的齐次变换矩阵。

15、在本发明的一种实施方式中，基于所述红宝石测头的坐标系原点和所述标准球的球心分别在机器人基坐标系下的位置，建立标定模型，包括：

16、以标准球为参考目标，建立标定模型为：

17、

18、其中，为红宝石测头的坐标系原点tcp在机器人基坐标系{b}下的位置；是标准球的球心在机器人基坐标系{b}下的位置，其数值未知；r和r分别是标准球的半径和红宝石测头的半径。

19、在本发明的一种实施方式中，所述目标函数为：

20、

21、。

22、在本发明的一种实施方式中，所述红宝石测头的坐标系原点位置参数为，有如下关系：

23、，得：

24、，简化为：

25、；

26、其中，为机器人手腕末端的姿态矩阵，为机器人手腕末端的位置矩阵。

27、在本发明的一种实施方式中，基于所述目标函数，利用l-m方法与direct方法进行循环迭代计算，还包括：

28、设置l-m方法的迭代收敛条件、迭代终止的最小步长、最大迭代次数和最大循环次数；

29、每次迭代后，判断迭代步长是否小于最小步长；

30、若满足小于最小步长，则判断是否满足收敛条件，若满足收敛条件，则终止迭代，并输出目标函数的全局最优解，若不满足收敛条件，则输出目标函的局部最小值；

31、若不满足小于最小步长，则判断是否达到最大迭代次数；

32、若未达到最大迭代次数，则继续迭代计算；

33、若达到最大迭代次数，则停止迭代，输出结果。

34、在本发明的一种实施方式中，当输出目标函的局部最小值时，判断是否达到最大循环次数，若达到，则结束循环，若未达到，将局部最小值作为direct方法的初始参数。

35、在本发明的一种实施方式中，所述迭代收敛条件为迭代结果收敛至0.1mm以内。

36、在本发明的一种实施方式中，基于所述目标函数，利用l-m方法与direct方法进行循环迭代计算，还包括：

37、设置direct方法的迭代终止条件以及搜索范围控制参数，将通过l-m方法得到局部最小值作为direct方法的初始参数；

38、判断迭代计算得到的函数值小于局部最小值，若满足小于局部最小值，则更新l-m方法的初始参数，若不满足小于局部最小值，则判断是否满足迭代终止条件；

39、若不满足迭代终止条件，则继续迭代计算，若满足迭代终止条件，则判断是否达到最大搜索范围，若达到，则未搜索到最优解，输出结果，若未达到，则通过改变搜索范围控制参数的数值扩大搜索范围，重新迭代计算。

40、本发明还提供一种求解全局最优的组合式机器人接触式标定系统，包括：

41、齐次变换矩阵获取模块，用于获取在机器人的红宝石测头与标准球接触时，机器人手腕末端的坐标系到机器人基坐标系的齐次变换矩阵；

42、标定模型建立模块，用于基于所述红宝石测头的坐标系原点和所述标准球的球心分别在机器人基坐标系下的位置，建立标定模型；

43、目标函数建立模块，用于基于所述标定模型，根据非线性最小二乘优化方法，建立目标函数；

44、循环迭代计算模块，用于基于所述目标函数，利用l-m方法与direct方法进行循环迭代计算，得到所述目标函数的全局最优解；

45、位置参数获取模块，用于基于所述全局最优解，得到红宝石测头的坐标系原点位置参数。

46、本发明的上述技术方案相比现有技术具有以下优点：

47、本发明所述的一种求解全局最优的组合式机器人接触式标定方法及系统，考虑机器人测头tcp标定的实际特点，将l-m算法和direct算法组合得到优化算法即l-m-d算法，该算法具有良好的全局收敛性和计算效率，与其他算法相比，l-m-d算法组合优化方法不依赖于初始值，具有全局优化能力，迭代速度快，可以有效地解决机器人标定这类非线性方程系统问题。

48、该方法不需要一个比较准确地初始解，可已从任意位置开始迭代计算。当初始解不充分靠近问题解的情况下，也能快速收敛。且算法具有较好的鲁棒性，可以处理迭代矩阵病态的问题。

49、本发明结合两种算法的优势，通过组合算法来解决该问题。设计的算法采用l-m法与direct算法进行相互循环迭代获取全局最优的组合式算法。该方法兼顾l-m的局部搜索效率和direct的全局收敛性。整个组合算法由两个阶段步组成：局部极小化阶段和跳出局部极小值阶段。使用l-m法进行局部最优化，使用direct算法来跳出局部最小值。