一种基于高阶扰动和灵活三元正则化的协同矩阵分解的LncRNA-疾病关联预测方法

本发明涉及矩阵分解与生物基因结合，具体为一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法。

背景技术：

1、非编码rna(ncrna)根据在核苷酸数量主要分为small rna、medium rna和长非编码rna(lncrna)，其中长非编码rna在动植物的疾病表达调控上起着相当重要的作用。目前的生物研究表明，在肺腺癌疾病的发展过程中，长链非编码rna haglr抑制了肿瘤的生长，因此该lncrna被人们确认为肿瘤抑制因子。同时在食管癌疾病的研究中，lncrna(adamts9-as2)可以有效地抑制该癌细胞的增殖、侵袭和迁移。由此可见，对lncrna-疾病潜在关联的研究有助于人类在相关疾病上的预防、检测和治疗。传统的生物实验方法在发现潜在相关性方面具有较高的准确性，但过程复杂且耗时。因此，基于目前快速发展的计算机技术去开发一种高效、方便的计算方法用于检测lncrna与疾病之间的关联性具有重要意义。

2、已知lncrna-疾病关联矩阵的有效信息非常稀疏，大部分lncrna仅与单一疾病存在关联，这意味着lncrna与疾病的整体数量较大但它们之间的交互信息又过少，这种情况往往会导致分解系统出现冷启动问题，不足的交互数据将导致难以构建完整准确的预测模型，简而言之，对于单一稀疏交互数据的lncrna(疾病)很难进一步挖掘其余从未接触过的疾病(lncrna)。以往处理冷启动问题的lncrna-疾病关联预测方法主要包括基于邻居作用谱均值增强信息和基于随机游走预处理的方法。现有技术中，通过使用邻居节点相互作用谱的均值来重新计算lncrna的相互作用图谱，从而有效缓解冷启动问题。然而，这种方法存在明显缺点，每个lncrna节点在增强信息的同时其自身独特的信息会被均值同化掉，这意味着一部分lncrna的有效信息被增强的同时会导致一些强相关性节点被削弱和弱噪声被放大的问题。使用邻居的相互作用谱的平均值来重新计算lncrna的相互作用图谱的做法主要是从lncrna相似性矩阵的角度出发从而获得一些未被挖掘的相似性信息，同时也从更为稀疏的已知关联矩阵的角度出发，基于随机游走的理论知识，模拟lncrna-疾病关联矩阵网络的不同概率节点的跳跃从而获取新的关联信息，而且使用随机游走的方法并不会破坏原关联矩阵的原始信息。但是这种方法也存着局限性，面对动态变化或噪声干扰的数据集时鲁棒性较差,基于随机的概率来推测lncrna-疾病发生交互的可能，容易产生错误的预测结果。总之，在冷启动的问题上，现有方法在增强有效信息的过程中无法有效地避免噪声对结果的影响，而且也没有考虑从高阶的角度去挖掘更深层次的有效信息。

3、在已有的应用于预测潜在关联的矩阵分解方法中，对lncrna和疾病的相似性的学习方法主要分为图正则化和二元正交拟合相似性两种相似性学习方法。图正则化的目的是保持lncrna(疾病)邻居节点之间的相似性，以便更好地预测lncrna-疾病之间的潜在的关联。在lncrna-疾病关联预测的图正则化基本都是基于k近邻(knn)构建的邻域图，其针对每个节点去规划好统一大小的领域范围，但是无法做到为每个节点规划好不同的领域范围，这导致了部分信息节点无法捕捉到邻居节点的局部最优分布。而且由于基于knn的图正则化方法是局部性的，它所学习到的非线性结构主要反映了节点在其局部邻域内的关系。然而，这种局部视角使得它无法充分捕捉相似性矩阵中的全局非线性结构信息，从而导致部分全局非线性信息丢失问题。二元正交拟合相似的方法相对于图正则化方式在保存局部特征结构方面有所不同，它更加重视相似性特征的全局性结构。然而，这种双因子正交分解的限制性较强。该方法试图通过少量线性组合来近似表示原始高维数据，因此无法有效地学习到相似性矩阵的非线性结构信息。无论是lncrna还是疾病的相似性矩阵的计算方法，往往都会对计算得到的相似性信息矩阵引入非线性结构。例如，语义相似性是基于图的数据结构来计算每个节点的语义值，图的复杂结构往往会导致相似性矩阵出现非线性结构。再如，表达谱的差异性和皮尔逊相关系数计算的过程中都会导致相似性矩阵呈现非线性结构。因此，二元正交拟合相似的方法用简单的线性组合来拟合具有非线性结构的相似性矩阵时，会造成较大的拟合误差，从而导致相似性信息的丢失。总之，能否精确地学习和保留住lncrna(疾病)的相似性信息，对lncrna-疾病的算法模型的表现性能至关重要。然而，目前基于图正则化和二元正交拟合相似性的模型方法都难以有效地学习到相似性矩阵的全局非线性结构信息，从而导致部分全局非线性相似性信息的丢失。因此，发明一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法。

技术实现思路

1、鉴于上述和/或现有一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法中存在的问题，提出了本发明。

2、因此，本发明的目的是提供一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法，能够解决上述提出现有的问题。

3、为解决上述技术问题，根据本发明的一个方面，本发明提供了如下技术方案：

4、一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法，其包括具体步骤如下：

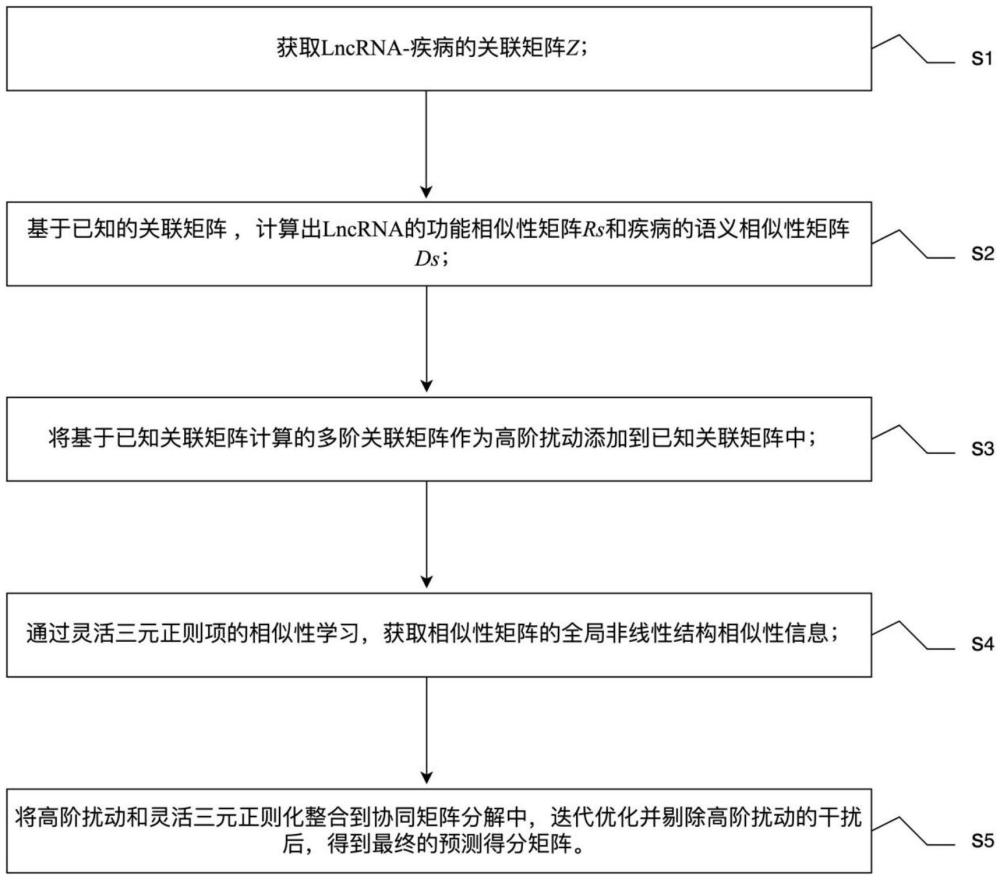
5、s1：获取lncrna-疾病的关联矩阵z；

6、s2：基于已知的关联矩阵z，计算出lncrna的功能相似性矩阵rs和疾病的语义相似性矩阵ds；

7、s3：将基于已知关联矩阵计算的多阶关联矩阵作为高阶扰动添加到已知关联矩阵中；

8、s4：通过灵活三元正则项的相似性学习，获取相似性矩阵的全局非线性结构相似性信息；

9、s5：将高阶扰动和灵活三元正则化整合到协同矩阵分解中，迭代优化并剔除高阶扰动的干扰后，得到最终的预测得分矩阵。

10、作为本发明所述的一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法的一种优选方案，其中：所述s1中其lncrna-疾病的关联矩阵z的获取步骤具体如下：

11、s11：第一个数据集来源于lncrnadisease2.0；

12、s12：为了便于对预测结果进行深入的案例分析，使用标准的mesh疾病术语和更广泛的类别术语替代原始数据集的术语；

13、s13：对数据进行清洗，删除重复的条目和非人类lncrna与疾病的条目，最终整理得到1690个经过生物实验确认过的lncrna-疾病的关联对，涵盖447种lncrna和218种疾病，将其作为实验的数据集，在此基础上，被定义的lncrna和疾病的关联矩阵z表达式如下：

14、

15、作为本发明所述的一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法的一种优选方案，其中：所述s2中疾病的语义相似性矩阵ds的计算步骤具体如下：

16、s21：基于mesh数据库构建有向无环图(dag(d)＝(t(d)，e(d)))，其中t(d)表示包括疾病d自身在内的疾病祖先节点集合，并且e＝(d)表示该疾病节点的祖先节点直接连接子节点的边集合；

17、s22：根据构建好的dag评判疾病本身和其祖先节点对自己的贡献度，其方程表达式如下所示：

18、

19、其中疾病t∈t(d)；

20、s23：疾病的语义值得分能够使用下面公式计算得到：

21、

22、s24：在此基础上，计算出疾病di和疾病dj之间的语义相似性，从而得到最后的疾病语义相似性矩阵ds：

23、

24、作为本发明所述的一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法的一种优选方案，其中：所述s2中lncrna的功能相似性矩阵rs的计算步骤具体如下：

25、s25：假设di和dj分别是与lncrna的ri和rj相关的疾病组；

26、s26：lncrna功能相似性矩阵定义为rs；

27、s27：ri和rj之间的相似性值计算如下：

28、

29、

30、其中|di|表示ri与疾病有关联的数量，|dj|表示rj与疾病有关联的数量，s(dm,dj)是跟lncrna的ri有关联的疾病dm和跟lncrna的rj有关联的疾病集dj之间的相似性。

31、作为本发明所述的一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法的一种优选方案，其中：所述s3中将基于已知关联矩阵计算的多阶关联矩阵作为高阶扰动添加到已知关联矩阵中的具体步骤如下：

32、s31：基于已知关联矩阵构建高阶连接矩阵c：

33、c＝min(1,zt·z)

34、其中是已知关联矩阵，zt·z就是代表了lncrna与疾病能够发生交互的媒介，为了避免数值差异导致后续分析的误差，将所有大于1的值限制为1，从而构建一个高阶连接矩阵c，这个二值矩阵矩阵代表了lncrna与疾病是否能够发生交互；

35、s32：基于高阶连接矩阵c构建不同阶的关联矩阵：

36、hyperconnection(z，i)＝min(1,z·ci-1)

37、在数据集的实验中观察到在4阶关联矩阵之后出现的高阶关联矩阵基本保持不变，为此只采用2-4阶的高阶关联矩阵作为最终高阶关联矩阵

38、

39、s33：计算出高阶扰动矩阵hop：

40、

41、s.t.w＝0.1*rand(size(z))；

42、其中⊙表示矩阵的哈达马积，随机值w表示高阶关联矩阵确定的位置可能发生交互的概率大小，在构建高阶关联矩阵时，仅在除原关联矩阵z之外的确定位置，即的值不为0的位置添加随机值w，因为原始关联矩阵z的有效信息在被保留的同时也要避免高阶关联矩阵处理对原矩阵产生影响，为了确保原始矩阵中关联信息的重要性得以保留，同时使设置的初始值与原矩阵的值有所区别，需将随机值w的范围设定在0到0.1之间，以确保其在减少对原矩阵干扰的同时能够有效反映关联的可能性；

43、因此，新的关联矩阵能够表示为：

44、znew＝z+hop。

45、作为本发明所述的一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法的一种优选方案，其中：所述s4中获取相似性矩阵的全局非线性结构相似性信息的具体步骤如下：

46、s41：基于协同矩阵分解的原理，针对lncrna与疾病的关联预测问题，设计协同矩阵分解的表达式：

47、

48、其中α1、α2和λ是正则项的超参数；

49、s42：在二元正交的两个变量中间添加额外的附加因子m和n，为相似性的学习保留全局非线性结构信息，因此，具有灵活三元正则化的矩阵分解的表达式如下：

50、

51、其中，和是附加到lncrna和疾病相似性正交变量上的因子矩阵，σ是控制附加因子m和n的超参数，为了避免在最小化目标函数时出现复杂的非凸耦合项，引入惩罚的代理矩阵变量使其近似于uvt，因此，上面公式也能够表达为：

52、

53、其中是uvt的代理矩阵变量。

54、作为本发明所述的一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法的一种优选方案，其中：所述s5中将高阶扰动和灵活三元正则化整合到协同矩阵分解中的具体步骤如下：

55、s511：基于高阶扰动和灵活三元正则化，提出的具有高阶扰动和灵活三元正则化的矩阵分解的具体目标函数最终表示如下：

56、

57、

58、s512：为了避免在求解目标函数最小化问题时出现繁琐的非凸耦合项，同时减少因变量次方数过高而带来的优化难度，引入和两个变量，分别用于拟合um和vn；

59、s513：最终，经过这些变换，上面的目标函数也能够表示为：

60、

61、

62、同样地，β1以及β2也是一组超参数。

63、作为本发明所述的一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法的一种优选方案，其中：所述s5中迭代优化的具体步骤如下：

64、s521：更新x

65、

66、

67、

68、s.t.r∈(0,2),s>0,y≥0

69、其中，矩阵b和y是梯度下降过程中用于过渡的临时矩阵变量，s是迭代过程的一个超参数，r是梯度步长，为了简化实验过程并避免引入过多的超参数，同时确保优化算法的收敛性，将r的取值设定为0.1；

70、s522：更新u

71、

72、令：

73、

74、则：

75、

76、

77、

78、s.t.s>0,up＝ut-1

79、up代表u的上一个迭代数据ut-1，e是一个单位矩阵；

80、s523：更新v

81、

82、基于u的更新公式，能够类比推理得：

83、

84、

85、s.t.s>0,vp＝vt-1

86、同样地，vp代表v的上一个迭代数据vt-1；

87、s524：更新w

88、

89、

90、

91、s.t.r∈(0,2),s>0,y≥0

92、其中，矩阵t和y是梯度下降过程中用于过渡的临时矩阵变量；s525：更新q

93、

94、令：

95、

96、则：

97、

98、q＝(β1um+α1rsu)(β1e+α1utu)-1；

99、s526：更新p

100、

101、令：

102、

103、则对因子矩阵p的偏导为：

104、

105、基于q的更新公式步骤同样能够类比推理得到：

106、p＝(β2vn+α2dsv)(β2e+α2vtv)-1；

107、s527：更新m

108、

109、令：

110、

111、则：

112、

113、m＝(β1utu+σe)-1(β1utq)；

114、s528：更新n

115、

116、令：

117、

118、则：

119、

120、基于m的优化步骤，能够类比推理得：

121、n＝(β2vtv+σe)-1(β2vtp)。

122、作为本发明所述的一种基于高阶扰动和灵活三元正则化的协同矩阵分解的lncrna-疾病关联预测方法的一种优选方案，其中：所述s5中最终的预测得分矩阵的具体得到步骤如下：

123、s531：在迭代过程满足以下条件后：

124、

125、s532：计算得到近似的得分矩阵：

126、

127、s533：在剔除高阶扰动对结果的影响之后，得到最终的得分矩阵：

128、

129、与现有技术相比：

130、本发明在矩阵分解阶段对原已知关联矩阵进行高阶连接处理获得高阶关联矩阵，在原已知关联矩阵中添加了高阶信息作为“新”的关联交互信息，增加了lncrna(疾病)具有跟目前没有交互的疾病(lncrna)产生发生联系的可能性，其次在二元正交法中的二元变量中间添加附加因子进一步提供必要的自由度，以获得良好的因子分解，附加因子可以揭示相似性信息在不同的行与列簇相关性，从而提供lncrna与疾病能够发生交互的沟通桥梁，进而学习到相似性矩阵的全局非线性结构，获取更加完整的相似性信息；最后基于协同矩阵分解的方法对目标函数进行优化迭代得到最后的预测得分矩阵，使得最终预测lncrna-疾病的关联更加准确。