一种基于牛顿-拉夫逊优化算法的切负荷方法与流程

本发明涉及电网切负荷领域，具体的说，涉及一种基于牛顿-拉夫逊优化算法的切负荷方法。

背景技术：

1、随着智能电网的深化建设，配电网系统迫切需要更精确的精准切负荷策略来维护电网的最后一道安全屏障，保证负荷用电的可靠性。我国部分电网已经建成了大规模精准负荷控制系统，控制精度可以达到用户下的1个分路开关上的可中断负荷量。在系统层面确定负荷节点或负荷控制子站的负荷控制量后，需要进一步将该控制量进行分解，确定底层各个用户的可中断负荷切除量，并通过负控终端实施负荷切除，其会精确到用户的可控分路开关。

2、首先，现阶段的研究和工程实践主要是对用户的可中断负荷按照最小控制误差原则或者经济最低损耗原则进行切除，忽略了公平性。

3、其次，在众多切负荷方法中，元启发式算法具有解决非线性问题的强大能力。如常用的粒子群优化(pso)算法、萤火虫优化(fa)算法。而牛顿-拉夫逊优化算法(nrbo)具有进化能力强、搜索速度快、寻优能力强的优点。其灵感来源主要基于两个关键原理：newton-raphson搜索规则(nrsr)和陷阱避免算子(tao)。nrsr使用newton-raphson方法来提高nrbo的探索能力，并提高收敛速度以达到改进的搜索空间位置。tao有助于nrbo避免局部最优陷阱。

技术实现思路

1、针对上述现有技术的不足，本发明所解决的技术问题在于如何同时考虑经济性与公平性为目标函数进行切负荷优化，并且基于牛顿-拉夫逊优化算法求得最优，避免之前大多智能优化算法都存在的局部最优问题。本发明分别从切负荷思路上和切负荷算法上进行创新。

2、实现本发明的技术思路是：本发明将精准切负荷问题建模成一个单目标多约束优化问题。考虑将经济性与公平性作为目标函数，把切负荷精确度约束、切负荷量约束、负荷重要程度约束作为约束条件，建立一个切负荷优化模型；本发明引入牛顿-拉夫逊优化算法解决上述建立的切负荷优化模型，牛顿-拉夫逊优化算法具有搜索速度快、寻优能力强、能避免解决局部最优的特点，它在面对大规模切负荷任务时可以根据问题的复杂度和规模进行自动调整搜索策略。

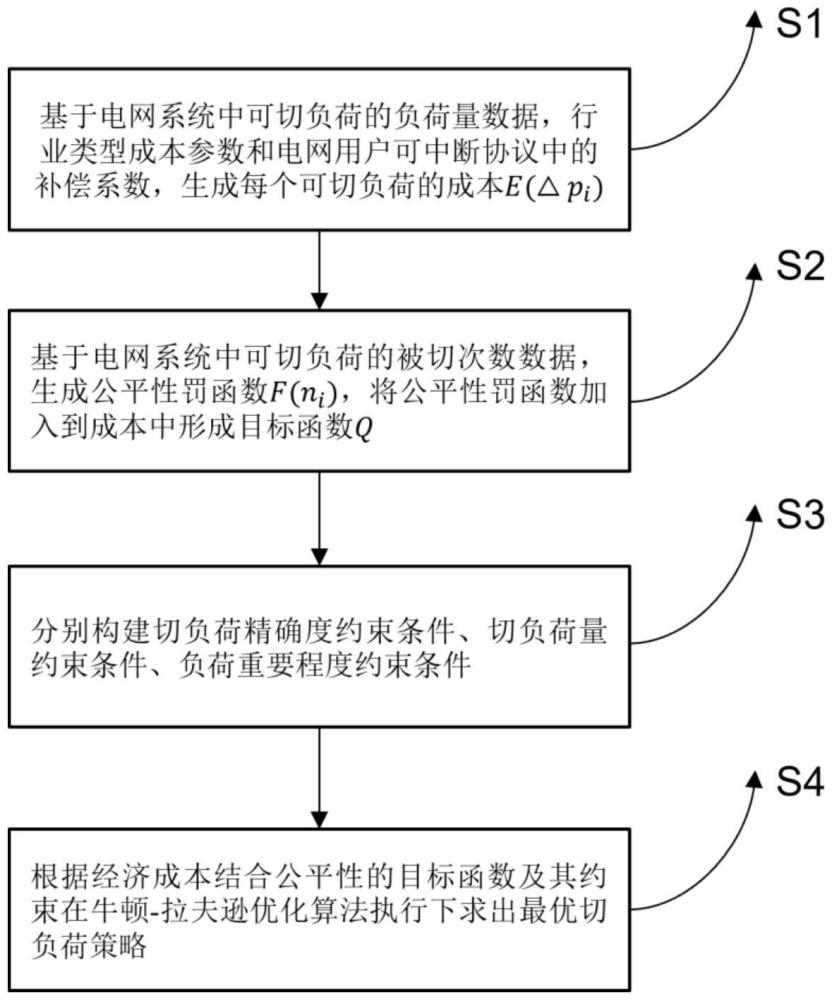
3、本发明的步骤如下：

4、s1：基于电网系统中可切负荷的负荷量数据，行业类型成本参数和电网用户可中断协议中的补偿系数，生成每个可切负荷的经济成本e(△pi)。

5、

6、其中，△pi表示可切负荷qi的负荷量，为常系数，由行业类型确定，为电网用户可中断协议中的补偿系数。

7、s2：基于电网系统中可切负荷的被切次数数据，生成公平性罚函数f(ni)，将公平性罚函数加入到经济成本中形成目标函数q。

8、s2.1：基于可切负荷的被切次数数据对可切负荷qi的公平性进行计算，生成公平性罚函数，公平性罚函数为：

9、

10、其中，ni表示可切负荷的被切次数，nmax表示所有可切负荷中最大的被切次数；

11、s2.2：将公平性罚函数加入到s1构建的经济成本函数中形成目标函数，目标函数为：

12、

13、其中，n表示系统中可切负荷数，xi＝{0,1}，xi＝1表示要切除qi负荷，xi＝0表示不切除qi负荷，λ为权重比例。

14、s3：分别构建切负荷精确度约束条件、切负荷量约束条件、负荷重要程度约束条件。

15、s3.1：构建切负荷精确度约束条件。

16、所述切负荷精确度约束条件如下：

17、

18、β∈[0,βmax]

19、其中：β为精度值，比如设置为5％，βmax表示最大精度值，△p表示下达命令要切的负荷量。

20、s3.2：构建切负荷量约束条件。

21、所述切负荷量约束条件如下：

22、

23、表示系统中所有可切负荷的负荷量总和，下达命令要切的负荷量要小于等于系统中所有可切负荷量的总和。

24、s3.3：构建负荷重要程度约束条件。

25、由于不同负荷节点在电网中的重要程度不一，因此负荷重要程度约束条件可设置为：

26、l(i|xi＝1)≥l(j|xj＝0)

27、其中：l(i)表示负荷qi的重要值，重要值越大则负荷越不重要。l(i|xi＝1)表示被选中要切掉的负荷qi的重要值，l(j|xj＝0)表示没被选中切掉的负荷qj的重要值。

28、s4：根据经济成本结合公平性的目标函数及其约束在牛顿-拉夫逊优化算法执行下求出最优切负荷策略。

29、s4.1：初始化牛顿-拉夫逊优化算法的种群。

30、s4.2：根据牛顿-拉夫逊搜索规则((nrsr)进行迭代更新种群位置。

31、s4.2.1：使用数学nrm(牛顿-拉夫逊方法)来代替函数的显式公式，解决许多优化方法是不可微的问题，得到nrsr。

32、s4.2.2：设置参数δ。

33、s4.2.3：确定参数ρ的值。

34、s4.2.4：将位置xn-δx替换为位置xb。

35、s4.2.5：确定并更新向量和的当前位置。

36、s4.2.6：确定并更新的位置。

37、s4.3：在迭代种群寻优过程中，使用陷阱避免操作员(tao)避免陷入局部最优。

38、s4.4：判断是否达到最大迭代次数，如果是的话将种群最优位置xb作为切负荷结果输出，否则回到步骤s4.2，继续迭代。

39、本发明的有益效果为：

40、1.建立切负荷目标函数时，基于电网系统中可切负荷的被切次数数据，生成公平性罚函数，将公平性罚函数加入到切负荷经济成本中形成目标函数，使得切负荷方法的设计更合理。

41、2.基于牛顿-拉夫逊优化算法求解切负荷问题，牛顿-拉夫逊优化算法具有比传统的粒子群优化算法、萤火虫优化算法等更好的优化性能，且能避免局部最优陷阱。

技术特征：

1.一种基于牛顿-拉夫逊优化算法的切负荷方法，其特征在于，包括以下步骤：

2.根据权利要求1所述的一种基于牛顿-拉夫逊优化算法的切负荷方法，其特征在于，s1中，每个可切负荷的经济成本的计算表达式为：

3.根据权利要求2所述的一种基于牛顿-拉夫逊优化算法的切负荷方法，其特征在于，s2中，基于可切负荷的被切次数数据对可切负荷qi的公平性进行计算，生成公平性罚函数，公平性罚函数为：

4.根据权利要求3所述的一种基于牛顿-拉夫逊优化算法的切负荷方法，其特征在于，s3中，所述切负荷精确度约束条件如下：

5.根据权利要求4所述的一种基于牛顿-拉夫逊优化算法的切负荷方法，其特征在于，s4包括：

技术总结本发明提供了一种基于牛顿‑拉夫逊优化算法的切负荷方法，S1：基于电网系统中可切负荷的负荷量数据，行业类型成本参数和电网用户可中断协议中的补偿系数，生成每个可切负荷的经济成本；S2：基于电网系统中可切负荷的被切次数数据，生成公平性罚函数，将公平性罚函数加入到经济成本中形成目标函数；S3：分别构建切负荷精确度约束条件、切负荷量约束条件、负荷重要程度约束条件；S4：根据经济成本结合公平性的目标函数及其约束条件在牛顿‑拉夫逊优化算法执行下求出最优切负荷策略。本发明建立切负荷目标函数时，基于电网系统中可切负荷的被切次数数据，生成公平性罚函数，并将其加入到切负荷经济成本中形成目标函数，使得切负荷方法的设计更合理。技术研发人员：魏翔,周洋,杨燕,王华,刘秋明,肖子洋,周炜煜,杨涛,钟华,元帅,白亚新,李子晖,陈龙平受保护的技术使用者：国网江西省电力有限公司信息通信分公司技术研发日：技术公布日：2024/9/2