判断顶点与几何体空间位置的方法及单元属性赋值方法与流程

本发明涉及工业数值仿真，尤其涉及一种判断顶点与几何体空间位置的方法及单元属性赋值方法。

背景技术：

1、在工业数值仿真过程中，单元属性赋值一般位于网格剖分步骤之后，具有重要意义。通过为每个网格单元分配正确的物理和数学属性，如材料属性、单元类型等，可以确保仿真模型能够准确反映实际系统的行为和性能。准确的单元属性赋值有助于减少仿真计算中的误差和不确定性，从而提高仿真效率，节省计算资源和时间，使工程师能够更快地得到仿真结果并进行进一步的分析和优化，加速产品开发周期。

2、在单元属性赋值时，则通常需要考虑点与几何体的空间位置关系。这种空间位置关系的判断对于确保单元属性赋值的准确性和合理性至关重要。在网格剖分过程中，会生成大量的网格单元，这些单元由一系列的点（顶点）定义。对于每个网格单元，需要判断其是否位于特定的几何体内或与之相交，这一步通过比较网格单元的顶点与几何体的边界来确定。如果网格单元的所有顶点都位于几何体外部，则该单元与几何体相离，不应被赋予该几何体的属性；如果网格单元与几何体有公共点或公共边界，则该单元与几何体相交，需要根据具体的仿真需求来决定是否赋予该单元几何体的属性；如果网格单元完全位于几何体内部，则该单元被几何体包含，则该单元应被赋予几何体的属性。基于上述空间位置关系的判断，可以为每个网格单元分配正确的属性，从而确保仿真模型能够准确反映实际物理系统的材料和物理属性分布。

3、在二维，一个几何体可以用多边形作为边界线来表征。在三维，一个几何体可以用多面体作为边界面来表征。判断点和几何体之间的位置关系是计算机辅助设计（cad）和计算机辅助工程（cae）中经常遇到的问题，这个问题可以转化为判断点和二维多边形或三维多面体空间位置关系。

4、常规射线法通过记录射线（图2中带箭头水平线）与多边形或多面体的交点个数来判断射线端点是否位于二维多边形或三维多面体内，若交点个数为奇数则在内部，若交点个数为偶数则在外部。常规射线法无法处理一些特殊的情况，例如，如图3所示：射线①和射线②与多边形的交点数相同，但射线①端点位于多边形外，射线②端点位于多边形内；射线③和射线④与多边形的交点数相同，但射线④端点位于多边形外，射线③端点位于多边形内。因此，需要探索一种能够正确判断上述特殊情况的适用于点与几何体空间位置判断的改进射线法。

技术实现思路

1、本发明的目的在于，提供一种判断顶点与几何体空间位置的方法及单元属性赋值方法，以解决上述问题，可以解决常规射线法无法解决的一些特殊情况，从而准确判断顶点与几何体的空间位置。

2、本发明提出了一种判断顶点与几何体空间位置的方法，包括如下步骤：

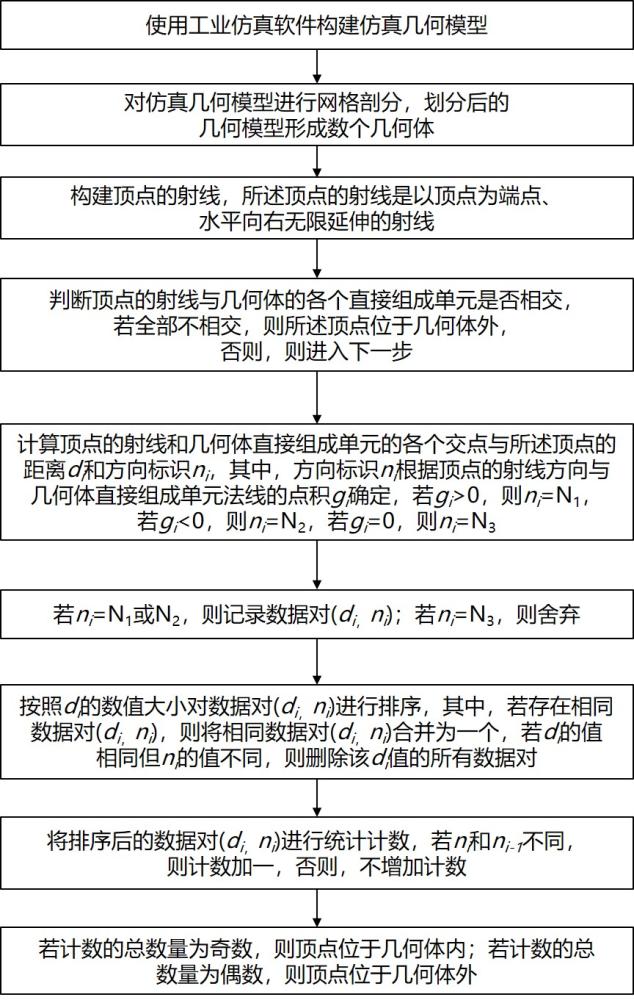
3、步骤s1、使用工业仿真软件构建仿真几何模型；

4、步骤s2、对仿真几何模型进行网格剖分，划分后的几何模型形成数个几何体；

5、步骤s3、构建顶点的射线，所述顶点的射线是以顶点为端点、水平向右无限延伸的射线；

6、步骤s4、判断顶点的射线与几何体的各个直接组成单元是否相交，若全部不相交，则所述顶点位于几何体外，否则，则进入步骤s5；

7、步骤s5、计算顶点的射线和几何体直接组成单元的各个交点与所述顶点的距离di和方向标识ni，其中，方向标识ni根据顶点的射线方向与几何体直接组成单元法线的点积gi确定，若gi>0，则ni=n1，若gi<0，则ni=n2，若gi=0，则ni=n3；

8、步骤s6、若ni=n1或n2，则记录数据对(di，ni)；若ni=n3，则舍弃；

9、步骤s7、按照di的数值大小对数据对(di，ni)进行排序，其中，若存在相同数据对(di，ni)，则将相同数据对(di，ni)合并为一个，若di的值相同但ni的值不同，则删除该di值的所有数据对；

10、步骤s8、将排序后的数据对(di，ni)进行统计计数，若ni和ni-1不同，则计数加一，否则，不增加计数；

11、步骤s9、若计数的总数量为奇数，则顶点位于几何体内；若计数的总数量为偶数，则顶点位于几何体外。

12、在一个实施例中，所述几何体为二维图形或三维几何体。

13、在一个实施例中，二维图形的直接组成单元为边，边是线段，边法线垂直于边并指向二维图形的内部。

14、在一个实施例中，所述判断顶点的射线与几何体的各个直接组成单元是否相交，具体包括：

15、分别计算和，

16、，

17、；

18、其中，a、b分别为二维图形一边的两端点，点a的坐标为（xa，ya），点b的坐标为（xb，yb），顶点s的坐标为（xs，ys），顶点的射线方向r为（xr，yr），r为单位向量；

19、若且，则顶点的射线与二维图形的边相交，否则，顶点的射线与二维图形的边不相交。

20、在一个实施例中，二维图形的边法线nab的计算公式为：

21、；

22、其中，a、b分别为二维图形一边的两端点，点a的坐标为（xa，ya），点b的坐标为（xb，yb）。

23、在一个实施例中，三维几何体的直接组成单元为面，面法线垂直于面并指向三维几何体的内部。

24、在一个实施例中，三维几何体的直接组成单元为三角面片。

25、在一个实施例中，所述判断顶点的射线与几何体的各个直接组成单元是否相交，具体包括：

26、分别计算和，

27、，

28、，

29、；

30、其中，；

31、；

32、；

33、a、b、c分别为三角面片的三个顶点，点a的三维空间坐标为（xa，ya，za），点b的三维空间坐标为（xb，yb，zb），点c的三维空间坐标为（xc，yc，zc），顶点s的三维空间坐标为（xs，ys，zs），顶点的射线方向r为（xr，yr，zr），r为单位向量；

34、若且，则顶点的射线与三角面片相交，否则，顶点的射线与三角面片不相交。

35、在一个实施例中，三角面片的面法线nabc的计算公式为：

36、；

37、其中，a、b、c分别为三角面片的三个顶点，点a的三维空间坐标为（xa，ya，za），点b的三维空间坐标为（xb，yb，zb），点c的三维空间坐标为（xc，yc，zc）。

38、本发明还提出了一种单元属性赋值方法，使用如上所述的判断顶点与几何体空间位置的方法判断网格单元的顶点与几何体的空间位置，若网格单元的顶点位于几何体内，则赋予该网格单元几何体的属性。

39、与现有技术相比，本发明的判断顶点与几何体空间位置的方法及单元属性赋值方法的有益效果在于：

40、1）本发明将几何体直接组成单元法线引入到射线法中，可以解决常规射线法无法解决的一些特殊情况，从而准确判断顶点与几何体的空间位置。

41、2）通过准确判断顶点与几何体的空间位置关系，可以确保仿真模型中的每个部分可以按照实际设计或物理状态进行精确建模，从而保证了仿真结果准确性，为后续分析提供可靠的数据，为工程决策提供有力支持。