一种3D芯片层间通孔布置方法

本发明涉及电子设计自动化领域，具体一种3d芯片层间通孔布置方法。

背景技术：

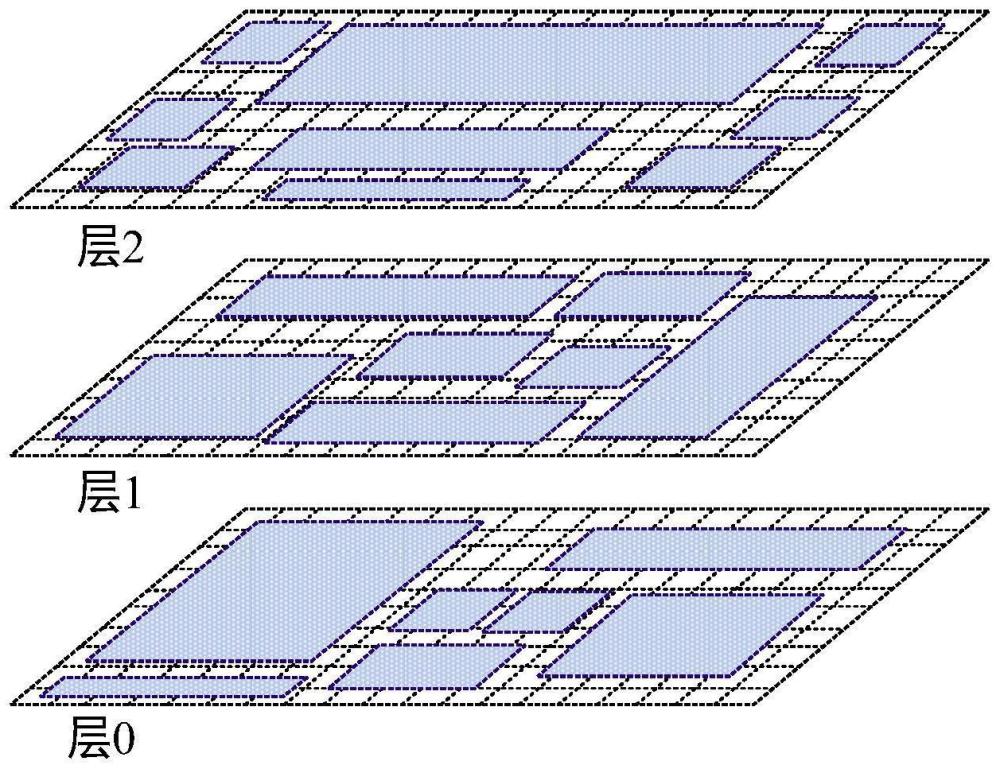
1、近年来，3d-ic(三维集成电路)技术因其在芯片设计方面的优势而吸引了大量关注。与传统的2d-ic(二维集成电路)相比，3d-ic可以提供更高的集成密度、更短的导线长度和更优的能效。要实现3d-ic设计，需要考虑的一个关键因素是不同层之间的信号传输。信号传输可以通过层间通孔，例如tsv(硅通孔)和miv(单片层间通孔)来进行。tsv是相对较大的垂直通孔，直径大约5微米，它们穿透硅基底与多个芯片层相连。最近，m3d(单片式三维集成电路)技术作为一种尖端方法出现，与基于tsv的3d-ic相比，m3d提供了更高的集成密度；m3d使用的miv直径小于100纳米，比tsv要小得多，如图1所示。m3d可以提供更小的3d接触间距和更高的集成密度，这对于开发紧凑型3d集成方案非常有帮助，同时高集成密度也给层间通孔布置算法的效率带来了挑战。

2、现有的解决通孔布置问题的方法中，均是将3d-ic芯片中的层间通孔布置问题建模为imcmc((最小费用多商品流)模型，并使用启发式方法来解决该imcmc问题。启发式方法在求解层间通孔布置问题时，先定义一组规则或启发式算法，这些规则是基于对问题结构的理解和特定的设计经验。例如，可以先布置对时序要求严格或信号完整性要求高的关键层间通孔，再安排其他层间通孔。此外，为了解决资源分配冲突和减少层间通孔间的干扰，可能会采用分层的方法，逐层进行优化，同时也可考虑使用模拟退火、遗传算法等全局优化技术来搜索潜在的布局空间。这些启发式方法通常需要迭代过程中不断调整参数，以逐步接近一个成本效益最佳的解决方案。

3、然而启发式方法往往需要对每个特定案例进行多次迭代和调整，这在面对紧迫的设计周期和复杂的设计要求时，可能导致计算时间大大增加，进而降低整体的求解效率。

技术实现思路

1、为解决上述问题，本发明提供一种3d芯片层间通孔布置方法。

2、该方法包括：

3、步骤一、定义c层目标芯片中所有n个需要连接的网络中第i个网络为nti，第i个网络nti对应的层间通孔集合为grii，第c层芯片中的第j个网格为层间通孔放置的目标是最小化成本函数cost；

4、步骤二、当3d芯片为两层芯片时，以每个网络需求的层间通孔为供应节点，以有空白区域的网格为需求节点，定义每个供应节点的供应量、每个需求节点的需求量，以及每个需求节点到每个资源节点的成本，构建最优传输模型；

5、步骤三、当3d芯片为多层芯片时，以网络的源点作为供应节点，以网络的汇点作为需求节点，以网格作为中转节点，以层间通孔作为商品，定义连接各种节点的边的容量和成本，以及每种节点的容量，构建整数最小费用多商品流模型；求解整数最小费用多商品流模型得到待调整布置方案；将待调整布置方案中每层的层间通孔作为供应节点，以该层的有空白区域的网格作为需求节点，构建每层的最优传输模型将待调整布置方案进行微调使每个节点满足容量限制；

6、步骤四、对最优传输模型的目标函数中引入熵正则化项后，通过sinkhorn的矩阵缩放算法求解最优传输模型的运输计划矩阵作为目标芯片的层间通孔的布置方案。

7、进一步的，步骤一中成本函数cost为：

8、

9、其中，代表第i个网络nti在第c层的子网，代表第i个网络nti在第c层联通需要布置的层间通孔的集合，为网络nti跨越的最底层，为网络nti跨越的最顶层，hpwl()代表半周长线长计算函数，代表网络nti在第c层的子网与该子网连通需要布置的层间通孔的2d边界框的半周长线长。

10、进一步的，步骤二具体指当3d芯片为两层芯片时，按照以下方式构建最优传输模型：

11、以每个网络需要的一个层间通孔作为一个供应节点，每个供应节点的供应量都设为1；

12、以每个有空白区域的网格作为一个需求节点，每个需求节点的需求量设为该需求节点所代表的网格的容量；

13、供应节点pi到需求节点qj的代价ai,j设为第i个网络nti需要的层间通孔布置在第j个空白网格上所需花费的线长成本ai,j：

14、

15、其中，代表第一层芯片中的第j个空白网格，代表第i个网络nti在第零层的子网，代表第i个网络nti在第一层的子网。

16、进一步的，当3d芯片为两层芯片时，在构建好的最优传输模型中引入一个虚拟供应节点，该虚拟供应节点的供应量设为所有需求节点的需求量与所有供应节点的供应量的差，该虚拟供应节点到每个需求节点的成本设为一个相同的常数。

17、进一步的，步骤三中所述以网络的源点作为供应节点，以网络的汇点作为需求节点，以网格作为中转节点，以层间通孔作为商品，定义连接各种节点的边的容量和成本，以及每种节点的容量，构建整数最小费用多商品流模型，具体指通过以下方式构建费用多商品流模型的有向图：

18、构建有向图g(v,e)，其中点集v包括源点汇点以及非零空白网格点si代表第i个网络nti的源点，ti代表第i个网络nti的汇点，代表目标芯片中的第c层中的第j个网格，一个源点与一个汇点间的连接方案代表一个网络的层间通孔布置方案；

19、边集包括{s→vg}，代表源点指向非零空白网格点的边；{vg→vg}，代表非零空白网格点指向另一个非零空白网格点的边；{vg→t}，代表非零空白网格点指向汇点的边；

20、对于非零空白网格点的容量设置为其对应的网格实际可容纳的层间通孔数量，其他类型的点的容量设为无穷大；

21、对于源点到非零空白网格点的边，以及非零空白网格点到汇点的边，将其容量定义为1，其他类型的边容量设为无穷大；

22、对于非零空白网格点指向汇点的边，其代价设为0，对于指向第c层中的第j个网格的边，如果第i个网络nti在第c层需要布置一个层间通孔，则指向的边的代价为：

23、

24、其中，代表第i个网络nti在第c层的子网，代表第i个网络nti在第c层联通需要布置的层间通孔的集合。

25、进一步的，步骤三中所述求解整数最小费用多商品流模型得到待调整布置方案，具体包括：

26、使用最短路径算法并行求解图g中的所有源点与汇点间的最短路径；

27、其中，对于第i个网络nti，通过最短路径算法求解得到的最短路径上遍历的网格单元集合为网络nti的待调整最短路径所有网络的待调整最短路径即构成了层间通孔的待调整布置方案。

28、进一步的，步骤三中所述将待调整布置方案中每层的层间通孔作为供应节点，以该层的有空白区域的网格作为需求节点，构建最优传输模型，具体包括：

29、定义对待调整布置方案进行微调后得到的最终的布置方案为

30、对待调整布置方案进行微调的优化目标为：

31、

32、其中，tc代表需要在第c层放置通孔的网络的集合，代表tc中的层间通孔从待调整位置到最终位置的曼哈顿距离之和；

33、将每个视为一个独立的最优运输实例，将对待调整布置方案进行微调的问题建模为最优传输模型，其中，对于层c，以通过该层的层间通孔为供应节点，以该层的有空白区域的网格作为需求节点，每个供应节点的供应量都设为1，每个需求节点的需求量设为该需求节点对应的网格的容量，单位成本设为

34、进一步的，步骤四中所述对最优传输模型的目标函数中引入熵正则化项，具体包括：

35、定义最优传输模型的目标函数为：

36、

37、h(f)＝-∑i,jfi,jlogfi,j；

38、其中，ai,j代表供应节点pi到需求节点qj的代价，供应节点pi到需求节点qj的运输量fi,j代表在当前层对应的最优传输问题中，第i个网络nti对应的层间通孔分配到第j个空白网格上的通孔数量，f代表由运输量fi,j组成的运输计划矩阵，λ为正的正则化参数，h(f)为运输计划矩阵f的熵。

39、进一步的，步骤四中所述通过sinkhorn的矩阵缩放算法求解最优传输模型的运输计划矩阵，具体包括：

40、将最优传输模型的供应节点、需求节点、成本矩阵和正则化参数λ作为python库pot中的函数输入，对运输计划矩阵f进行求解，得到一个近似解运输计划矩阵f′。

41、进一步的，得到近似解运输计划矩阵f′后，按照以下方式进行优化：

42、将近似解运输计划矩阵f′视为概率矩阵，其中每个元素代表对应的层间通孔被分配到对应的网格的几率；

43、基于一个网络对应的边界框的大小对层间通孔排序，一个网络的边界框的面积越小，则其优先级越高；

44、先放置优先级高的网络的层间通孔，再放置优先级低的网络的层间通孔，在放置层间通孔时优先放置进近似解运输计划矩阵f′中的概率最大且符合网格容量要求的网格，直到得到最终的层间通孔部署方案。

45、本技术实施例中提供的一个或多个技术方案，至少具有如下技术效果或优点：

46、本发明将3d-ic设计中层间通孔的部署进行建模，对于双层的3d-ic将其建模为最优传输问题，对于多层的3d-ic先将其建模为imcmc问题，通过gpu使用最短路径算法并行求解imcmc问题中的所有源点与汇点间的最短路径，得到满足线长最优的待调整布置方案，再将对待调整布置方案的调整进一步建模为最优传输问题以满足网格容量限制，最后求解最优传输问题得到最终的层间通孔部署方案。通过将多层的3d-ic中的层间通孔部署问题拆解为能够并行处理的最短路径计算，极大地提高了高集成密度3d-ic中层间通孔的布置方案的计算效率。