一种高精度惯性导航系统的重力扰动补偿方法
- 国知局
- 2024-10-09 15:11:37
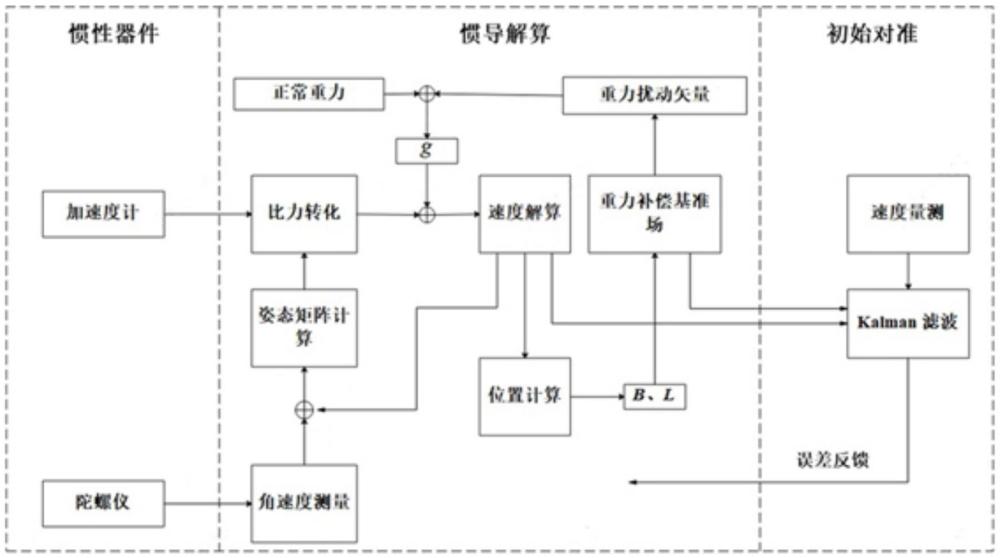
本发明涉及数据测绘的,尤其涉及一种高精度惯性导航系统的重力扰动补偿方法。
背景技术:
1、惯性导航系统(inertial navigation system,ins)不依赖任何外界信息,是一种自主式、隐蔽式高精度导航定位系统,具有全天候、不受外部干扰的优点。在包括惯性器件等误差的共同影响下,惯性导航系统误差随时间累积,严重地制约了潜航器水下长航时导航能力。在中低精度的惯性导航系统中,由于惯性器件精度相对较低,惯导解算所需的重力加速度一般采用正常重力模型计算的正常重力,然而由于地球质量分布不均匀,实际重力并不等于正常重力,还应包括重力扰动矢量(或垂线偏差)。因此采用正常重力模型来进行惯导解算是不精确的,重力扰动矢量的缺失会引起惯性导航系统误差,但在中低精度惯性导航系统中,惯性传感器带来的系统误差为惯导系统的主要误差源,而重力扰动对惯性导航系统定位精度的影响远小于惯性传感器的系统误差影响,因此,中低精度的惯性导航系统一般忽略重力扰动的影响而采用正常重力进行惯导解算。随着惯性导航器件以及旋转调制等系统补偿技术的发展和应用,我国惯性导航技术取得了突破性进展,尤其是旋转调制技术的发展和应用,使得我国惯性导航系统的精度得到大幅提升。原先所忽略的一些误差源成为制约ins精度进一步提升的关键,而重力扰动正是这类误差。重力扰动引起的系统误差已成为惯性导航框架内影响高精度惯导精度的主要误差源之一,为了满足水下长航时导航定位精度需求,对高精度惯性导航系统重力补偿技术深入研究,已成为当前水下auv高精度导航定位的迫切需求。
2、利用惯性导航重力补偿技术来进一步提高惯性导航框架内ins的导航定位精度,是当前水下导航领域的研究热点之一。通过利用高精度的重力扰动矢量补偿正常重力场模型引入的惯导误差,削弱重力扰动在惯性导航框架内对惯导精度的影响。当前惯性导航重力补偿技术方案主要有以下几种:
3、已有技术方案一:基于随机模型方法可从理论上分析重力扰动对惯性导航系统的影响误差并实现惯性导航系统的重力补偿。将重力扰动建模为高斯马尔科夫过程,可定量地评估重力扰动对惯性导航系统的影响,利用估计的重力扰动影响量对惯导的位置误差进行改正,以此实现重力补偿。随机模型方法可用于分析ins中未知重力扰动的误差传播及实现对重力扰动的预测和滤波。
4、然而,由于地球重力场(重力扰动、重力异常)的变化复杂性,单一的随机模型不足以描述重力场的变化规律;其次,为了精确估计随机统计模型的参数,必须提供大量的先验信息。因此,基于随机模型方法实现ins的重力补偿往往不是一种最佳的方案。
5、已有技术方案二:基于重力梯度仪的实时补偿方法,可实现惯性导航系统的力学编排。利用重力梯度仪器可以进行重力三维空间矢量的实时测量,将测量的重力矢量补偿到惯性导航系统的回路中可实现惯性导航系统的重力扰动补偿。
6、但是,仪器测量补偿技术需要搭载矢量重力仪或者重力梯度仪,鉴于仪器的稀缺性,对于一般的导航应用场景难以实现,因此,基于重力梯度仪的重力补偿方法目前很难普遍应用。
7、已有技术方案三:基于高阶重力场模型实现高精度惯性导航系统的重力补偿。随着超高阶地球重力场模型的发展,使得获取全球大范围的高精度重力扰动成为可能,基于全球重力场模型可确定任意位置的重力扰动,目前,普遍使用的高精度高阶地球重力场模型主要包含egm2008、eigen-6c4、geco、sgg-ugm-1和sgg-ugm-2等模型。将高阶重力场模型确定的水平重力扰动提供给ins,可改善ins的力学编排,当前利用高阶重力场模型实现惯性导航系统的重力补偿是最有效的技术方案。
8、但高阶重力场模型的最大阶次仅为2190,对于空间分辨率小于~10km的高频重力场信号,其仍然无法有效表示,即存在一定的截断误差。2190阶的重力场模型在全球范围内平均存在11.1mgal的重力异常以及1.7″的垂线偏差信号缺失,对地形起伏变化明显的地区,信号缺失更为严重。重力补偿技术的难点之一是在于获取高精度的重力扰动,现有的海洋重力补偿基准图主要是基于全球重力场模型构建,其精度和分辨率不足,对于低速运行的水下载体,重力扰动的高频信号对惯性导航系统的位置影响更为显著,基于全球重力场模型构建的重力补偿基准图难以满足更高精度的重力补偿需求。
技术实现思路
1、针对惯性导航系统误差受重力扰动影响的技术问题,本发明提出一种高精度惯性导航系统的重力扰动补偿方法,采用更适合的方法来实现惯性导航系统的重力补偿,完善水下重力辅助导航框架,旨在进一步提升惯性导航框架内的惯导定位精度。
2、为了达到上述目的,本发明的技术方案是这样实现的:一种高精度惯性导航系统的重力扰动补偿方法,具体步骤包括:
3、s1:对惯性导航的误差方程组进行解析,获得重力扰动影响下的惯性导航系统位置误差方程;
4、s2:根据重力扰动影响下的惯性导航系统位置误差方程,将重力扰动对惯性导航的位置影响建模为马尔可夫过程,建立水平重力扰动均方差、载体速度、空间波长与水平重力扰动引起的位置误差关系;
5、s3:利用重力扰动影下的惯性导航系统位置误差方程分析惯导重力补偿对重力扰动的精度和分辨率要求,利用重力场模型联合地形信息确定多频段重力扰动,将确定的重力扰动引入初始对准和惯导解算两个过程中实现重力补偿。
6、步骤s1所述获得重力扰动影响下的惯性导航系统位置误差方程的具体方法为:
7、s11:构建重力扰动影响惯性导航的误差影响方程;
8、s12:构建重力扰动影响惯性导航的误差影响方程的矢量形式,得到误差状态方程组;
9、s13:对误差状态方程组解析求解,得到重力扰动影响下的惯性导航系统位置误差方程。
10、步骤s11所述构建重力扰动影响惯性导航的误差影响方程的具体方法为:
11、误差影响方程包括速度误差影响方程和位置误差影响方程,考虑重力扰动的影响,惯性导航系统速度误差影响方程和位置误差影响方程表示为:
12、
13、
14、
15、式中,n表示导航坐标系,b代表载体坐标系,i代表惯性坐标系,e代表地球坐标系,为姿态坐标系到导航坐标系的旋转矩阵,δgn为重力扰动矢量,φ=[δα δβ δγ]为姿态误差,rn和rm分别为子午圈和卯酉圈的半径,为姿态误差φ的微分形式,fn为加速度计测量的比力在导航系下的投影,为加速度计的常值零偏,ve、vn和vu分别为东向、北向和天向速度,δvn=[δve δvn δvu]为载体在导航坐标系下的速度误差,是速度误差δvn的微分形式,b、l、h分别代表纬度、经度和高度,δb、δl和δh分别为纬度误差、经度误差和高度误差,和分别为纬度误差δb、经度误差δl和高度误差δh的微分形式,为导航坐标系下地球自转角速度,为导航坐标系相对于地球坐标系的转动角速度,为导航系下地球自转角速度误差,为导航坐标系相对于地球坐标系的转动角速度误差,为陀螺仪测量误差,为与之和。
16、步骤s12所述构建重力扰动影响惯性导航的误差影响方程的矢量形式的具体方法为:
17、导航坐标系下,地球自转角速度与导航坐标系相对于地球坐标系的转动角速度表示为:
18、
19、其中,r为地球平均半径,ω为地球自转角速度;
20、将速度误差影响方程、位置误差影响方程和转动角速度展开成矢量的形式,得到误差状态方程组:
21、
22、
23、
24、
25、
26、
27、
28、
29、
30、其中,δα,δβ,δγ分别是航向角误差、俯仰角误差和横滚角误差,分别是航向角误差、俯仰角误差和横滚角误差的微分形式,δve,δvn,δvd分别为北向、东向和天向的速度误差,δl,δλ,δh分别为纬度、经度及高度误差,r为地球的半径,δge、δgn、δgu分别为重力扰动在东西、北向和天向的分量,fe、fn、fu分别为加速度计在东向、北向、天向的测量比力。
31、步骤s13所述对重力扰动影响惯性导航的误差方程解析求解的具体方法为:
32、忽略陀螺测量误差和加速度计测量误差,设定初始的状态向量中姿态误差项为零以消除对准误差,将重力扰动等效为水平方向上的加速度计偏置,根据误差状态方程组计算生成基于北向单通道误差模型,并对基于北向单通道误差模型进行分析;
33、根据误差方程,北向单通道的误差动态性能用一组微分方程表示:
34、
35、
36、
37、
38、上式写成矩阵的形式,可变成:
39、
40、其中,状体转移矩阵f为:
41、
42、经过拉普拉斯变化求解状体转移矩阵f,得北向重力扰动影响的北向惯性导航系统位置误差方程:
43、
44、其中,δxn为北向位置误差,t为时间,ωs为舒勒频率。
45、步骤s2所述将重力扰动对惯性导航的位置影响建模为马尔可夫过程的具体方法为:
46、对重力扰动对惯性导航系统的频率影响特征进行分析,根据重力扰动影响下的惯性导航系统位置误差方程,重力扰动对惯性导航影响的马尔可夫关系表示为:
47、
48、式中,σ2为位置误差,是水平重力扰动的方差,ωs为舒勒频率,d为空间波长。
49、步骤s3所述将确定的重力扰动引入初始对准和惯导解算两个过程中实现重力补偿的方法为:
50、s31:利用重力扰动影下的惯性导航系统位置误差方程,基于重力场模型计算垂线偏差;
51、s32:基于地形信息的高频重力场建模;
52、s33:利用重力场模型联合地形信息确定多频段重力扰动,将确定的重力扰动引入初始对准和惯导解算两个过程中实现重力补偿。
53、步骤s31所述基于重力场模型计算垂线偏差的方法为:
54、根据重力场模计算垂线偏差可表示为:
55、
56、式中,gm为万有引力常数与地球质量的乘积,r计算点的向径,r为地球的平均半径,n和m分别为重力场模型的阶和次,nmax为重力场模型的最大阶次,和为完全标准化的球谐系数,λ和θ分别为经度和余纬,为完全标准化的勒让德函数。
57、步骤s32所述基于地形信息的高频重力场建模的方法为:
58、构建剩余地形模型,采用高分辨率地形/水深数据与参考地形做差获取剩余地形rtm,基于正演模型方法,计算rtm地形质量的引起的引力效应:
59、
60、其中,t是地形质量引力位,g为万有引力常数,r为积分点和计算点之间的距离,φ为体积,ρ为密度;
61、根据垂线偏差与引力位的关系,则垂线偏差表示为:
62、
63、γ为正常重力,ζrtm为子午圈垂线偏差分量,ηrtm为卯酉圈垂线偏差分量。
64、步骤s33所述利用重力场模型联合地形信息确定多频段重力扰动的方法为:
65、联合重力场模型和rtm技术确定垂线偏差,卯酉圈分量和子午圈分量分别表示为:
66、
67、上式中,ζrtm和ηrtm代表rtm计算的由于地形引起的高频部分,ζggm和ηggm分别为重力场模型计算的长波子午圈垂线偏差和卯酉圈垂线偏差分量;
68、根据垂线偏差与重力扰动的关系,东向和北向的重力扰动分别表示为:
69、δgn=-γ·ζ;
70、δge=-γ·η;
71、其中,δge为东向重力扰动,δgn为北向重力扰动。
72、本发明的有益效果为:
73、(1)本发明通过建立重力扰动影响下的惯性导航系统误差传播方程,从理论上定量解析重力扰动对惯导位置或速度的影响,分析重力扰动在惯导解算过程中的误差影响,建立重力扰动大小、重力扰动空间波长和惯导位置误差的模型,明确重力扰动影响高精度惯性导航系统的频率特征,揭示重力扰动对不同精度级别惯导的影响规律和影响量级,进一步判定惯导进行重力补偿的有效性。
74、(2)本发明对现有全球重力场模型进行误差分析及其频谱特征分析,以全球地形/水深数据为基础,基于全球地形/水深数据进行高频重力场信号建模,融合空间域和频谱域方法计算高频垂线偏差(或重力扰动矢量)信号,联合重力场模型与全球地形/水深数据正演的高频重力场信号精化高精度、高分辨率重力扰动,进一步提高了重力补偿中的重力扰动精度。
75、(3)在明确重力扰动对不同精度级别惯导影响规律及精化高精度重力扰动的基础上,将基于重力场模型联合地形信息确定的多频段重力扰动引入初始对准和惯导解算两个过程中实现重力补偿,进一步提升惯性导航系统重力补偿的有效性,增强水下潜器长航时导航能力,具有非常重要的军事战略意义和战略用途。
本文地址:https://www.jishuxx.com/zhuanli/20241009/308004.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 YYfuon@163.com 举报,一经查实,本站将立刻删除。
下一篇
返回列表