一种基于输入输出反馈线性化伺服压力机控制方法与流程

本发明属于电力电子与电机控制领域，具体涉及到一种基于输入输出反馈线性化伺服压力机控制方法。

背景技术：

1、传统的伺服压力机中电机控制方法主要是级联式的磁场定向控制，传统的级联式磁场定向控制是采用位置环pi、速度环pi、电流环pi，再加上坐标变换矩阵和svpwm进行控制，因此传统伺服压力机控制方法存在以下问题：

2、(1)伺服压力机的模型中转动惯量是典型的非线性，该问题会影响pi参数对系统的调节响应；

3、(2)如果单纯依靠运动学关系，不考虑力的关系传递和加速度的传递，只考虑位置的对应关系，系统的轨迹跟踪控制精度会变差。

技术实现思路

1、本发明为解决现有技术的不足，提供一种基于输入输出反馈线性化伺服压力机控制方法。

2、本发明是通过以下技术方案实现的：

3、一种基于输入输出反馈线性化伺服压力机控制方法，其特征在于：包括如下步骤：

4、步骤一：采用拉格朗日方程建立伺服压力机的动力学方程。

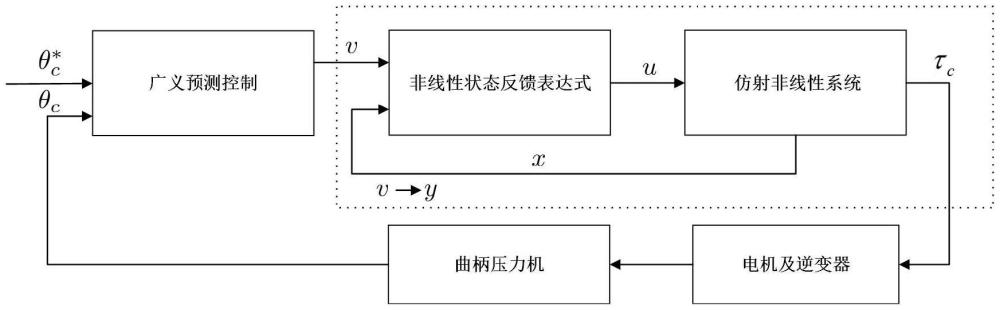
5、步骤二：将步骤一得到的伺服压力机的动力学方程按照微分同胚变换的仿射非线性系统进行表述，对输出函数y逐步求导，直至出现输入u，设计状态反馈v来消除非线性项，计算得到系统的非线性状态反馈表达式。

6、步骤三：采用广义预测控制算法作为整个系统的控制策略，控制模型采用受控自回归积分滑动平均过程模型，利用丢番图方程，得到广义预测控制算法的状态反馈v。

7、步骤四：将步骤三得到的状态反馈v代入步骤二系统的非线性状态反馈表达式得到u，用u除以减速机的减速比，得到电机给定转矩te*，通过电机给定转矩te*计算得到第k+1时刻电机的给定电流。

8、步骤五：根据定子电压方程计算第k+1时刻交轴电流的反馈值和第k+1时刻直轴电流的反馈值。

9、步骤六：将第k+1时刻电机的给定电流、第k+1时刻交轴电流的反馈值、第k+1时刻直轴电流的反馈值带入到模型预测电流控制一次价值函数中，并将模型预测电流控制一次价值函数取得最小值的电压矢量作用于功率模块，输出pwm波控制电机运行。

10、作为优选方案：

11、所述步骤一中，

12、利用拉格朗日方程建立伺服压力机的动力学方程：

13、

14、其中，τc是曲柄负载转矩；m(θc)是惯性系数；n(θc)是压力机的离心系数；为曲柄反馈角加速度；是曲柄反馈角速度。

15、所述步骤二具体包括以下步骤：

16、将伺服压力机的动力学方程经过变形可得：

17、

18、然后将公式(35)按照微分同胚变换的仿射非线性系统进行表述如下：

19、

20、y＝h (36)，

21、其中，h＝[x1](40)；u＝[τc](42)；其中，f和g是二阶系统上的光滑向量场；h是二阶系统上的光滑的标量函数；

22、对输出函数y逐步求导，直至出现输入u，

23、

24、设计状态反馈v：

25、

26、其中，β0、β1、β2均为配置参数；其中，

27、

28、得到系统的非线性状态反馈表达式：

29、

30、其中，

31、所述步骤三具体包括以下步骤：

32、状态反馈v的公式(53)可变换得到：

33、

34、将线性化后的系统式(55)经过拉式变换，可得传递函数为：

35、

36、以采样周期t对其采样保持，可由公式(56)得到离散传递函数：

37、

38、其中，b(z-1)＝b1z-1+b2z-2(62)；a(z-1)＝1+a1z-1+a2z-2(63)；a1、a2、b1、b2均为常数；ts表示控制周期；

39、控制模型采用受控自回归积分滑动平均过程模型，受控自回归积分滑动平均过程模型表达式为：

40、

41、其中，ξ表示均值为零，方差为σ2的白噪声；y(k)表示θc在k时刻的值；δ＝1-z-1；v(k-1)表示k-1时刻的v值；c(z-1)＝1；

42、利用丢番图方程可以得到领先j时刻的系统输出预测值，选择如下丢番图方程：

43、1＝ej(z-1)a(z-1)δ+z-jfj(z-1)(65)，

44、其中，ej(z-1)和fj(z-1)表示为由a(z-1)唯一决定的多项式，且预测长度为j；z-j表示离散域内滞后j个周期；

45、为了将k时刻以前和k时刻以后的输入控制信息分开表示，选择如下丢番图方程：

46、ej(z-1)b(z-1)＝lj(z-1)+z-jhj(z-1) (66)，

47、其中，lj(z-1)和hj(z-1)表示为由ej(z-1)b(z-1)唯一确定的多项式；

48、利用公式(64)和丢番图方程(65)和(66)可得到下式：

49、y(k+j)＝lj(z-1)δv(k+j-1)+hj(z-1)δv(k-1)+fj(z-1)y(k) (67)，

50、其中，y(k+j)表示领先j时刻的y值；v(k+j-1)表示领先j-1时刻的v值；v(k-1)表示k-1时刻的v值；

51、广义预测控制二次价值函数j表达式为：

52、

53、其中，n0表示系统第一步预测长度，n0＝1；n1表示系统预测长度；nu表示输入控制长度；λ表示权重因子；y*表示所希望的系统输出目标值；

54、将公式(67)代入公式(68)，然后让n1＝1，j＝1，可得到公式(69)：

55、

56、其中，f＝hj(z-1)δv(k-1)+fj(z-1)y(k)(70)；右上角的t均表示转置的意思；

57、从公式(69)取最小值，可进一步得到状态反馈v的计算式：

58、v(k)＝v(k-1)+(ljtlj+λ)-1ljt(y*-f) (71)，

59、其中，v(k)表示k时刻v的值。

60、所述步骤五具体步骤为：

61、定子电压方程为：

62、

63、其中：

64、ψd＝ldid+ψf (76)，

65、ψq＝lqiq (77)，

66、上述，vd是直轴电压；vq是交轴电压；id是直轴电流；iq是交轴电流；r是定子电阻；ωe是电角速度；ψd是直轴定子磁链；ψq是交轴定子磁链；ψf是永磁体磁链；ld是直轴电感；lq是交轴电感；

67、根据所述定子电压方程，利用欧拉前向逼近法则，利用第k时刻的电流值可计算得到第k+1时刻电流值：

68、

69、其中，iq(k)为第k时刻交轴电流的反馈值；iq(k+1)为第k+1时刻交轴电流的反馈值；id(k)为第k时刻直轴电流的反馈值；id(k+1)为第k+1时刻直轴电流的反馈值；ts为控制周期；vd(k)是第k时刻直轴电压；vq(k)是第k时刻交轴电压。

70、所述步骤六中，模型预测电流控制一次价值函数为：

71、g＝|iq*(k+1)-iq(k+1)|+|id*(k+1)-id(k+1)| (82)，

72、其中，id*(k+1)表示第k+1时刻直轴电流的给定值，id*(k+1)＝0。

73、本发明的有益效果：

74、本发明对伺服压力机进行动力学模型建模，采用输入输出反馈线性化的非线性系统控制方法，将具有仿射非线性系统的动力学模型转换为线性动力学模型，采用广义预测控制算法作为整个系统的控制策略，控制模型采用受控自回归积分滑动平均过程模型，通过线性控制方法完成对伺服压力机的精确轨迹控制，控制精度显著提高，并且适用各类传动结构的伺服压力机。