一种基于宽度神经网络的传感器初期漂移故障在线诊断方法

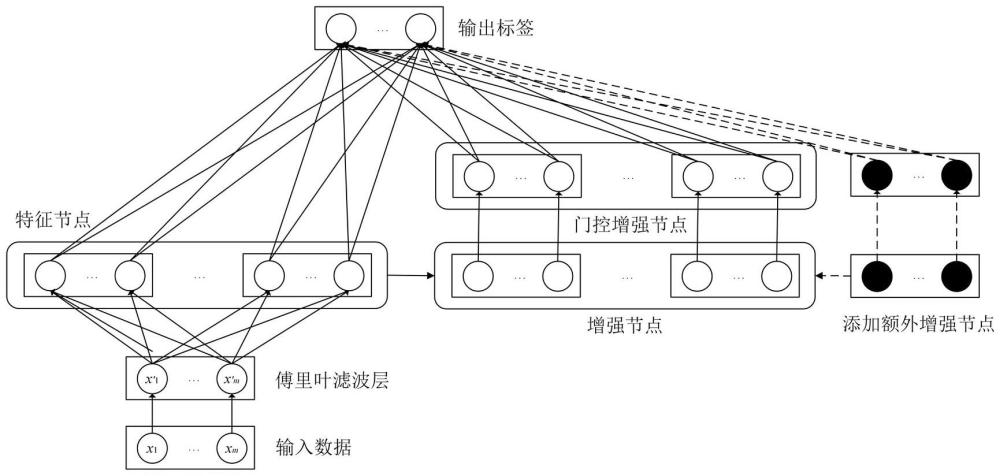
本发明是一种基于宽度神经网络的传感器初期漂移故障在线诊断方法，旨在实现对污水处理过程的传感器初期漂移故障进行在线诊断，包括检测故障发生时刻与定位故障传感器。

背景技术：

1、传感器是评估污水处理过程运行状况不可或缺的工具，其可靠性是确保污水处理厂安全和出水水质的先决条件。然而，由于高温、潮湿、腐蚀等环境条件及安装维护不当等因素，传感器极易出现故障。传感器故障可分为以下几类：漂移故障、偏差故障、精度下降故障、尖峰故障和卡死故障。其中，漂移故障是最常见的类型之一，其特点是随着时间的推移缓慢而渐进变化。随着漂移故障的发展，数据会显著失真，进而造成控制失败、出水水质不达标等灾难性影响。然而，重大故障通常不会突然发生，而是从初期故障演变而来。初期故障是指传感器开始恶化时的第一个变化点。漂移故障的初期阶段检测有助于及时采取补偿措施，控制故障的严重程度。因此，及时准确检测初期漂移故障发生时刻并定位故障传感器对于确保污水处理厂的安全运行至关重要。

2、目前，漂移故障初期诊断仍是一项重大挑战。首先，鉴于污水处理过程的非线性、强耦合、高时变等复杂特性，传感器的漂移故障诊断具有挑战性。其次，污水处理过程数据通常包含噪声，其特点是数据偶发尖峰或骤降，而初期漂移故障变化微弱。故难以区分故障和噪声，从而极易导致漏诊或误诊。因此，本发明提出一种基于宽度神经网络的传感器初期漂移故障在线诊断方法，实现污水处理过程传感器的初期故障诊断。

技术实现思路

1、本发明提出了一种基于宽度神经网络的传感器初期漂移故障在线诊断方法，根据实际污水处理过程采集的数据实现了在噪声存在情况下的多传感器初期漂移故障诊断。本发明不仅可以处理过程中的非线性和动态性，而且网络结构简单，更新速度快，检测精度高，可以实现污水处理过程传感器的在线监控。

2、本发明提出了一种基于宽度神经网络的传感器初期漂移故障在线诊断方法，该算法包括以下步骤：

3、一种基于宽度神经网络的传感器初期漂移故障在线诊断方法，其特征在于，包括以下步骤：

4、步骤1：建立基于傅里叶滤波器的特征层；

5、步骤1.1：在t时刻，输入由m维样本向量x(t)＝[x1(t),…,xm(t)]t表示；同时，整个样本序列通过滑动窗口机制输入基于傅里叶滤波器的特征层，样本序列描述为：

6、

7、其中，m代表样本维数，t0代表滑动窗口大小，取值范围为[5,30]的正整数；代表实数域；

8、步骤1.2：利用离散傅里叶变换，将第i维输入序列fi(t)转换到频域，得到第i维频域分量fi(t)如公式(2)：

9、

10、其中，f{}代表离散傅里叶变换，m代表样本维数，每维数据均通过公式(2)变换得到整体频率分量f(t)如公式(3)：

11、

12、其中，代表实数域；

13、步骤1.3：构建一个基于傅里叶的特征滤波器r(t)，如公式(4)：

14、

15、其中，w(r)为滤波器的权值，r∈[1,l]为滤波器的行序号，代表实数域，为单位矩阵，为全零矩阵，l代表滤波器的行数，由公式(5)计算：

16、l＝η×t0 (5)

17、其中，η为滤波率，取值范围为(0,1)；滤波器的输出信号见公式(6)：

18、

19、其中，f′(t)代表t时刻滤波后的样本；

20、步骤1.4：将f′(t)的每一维通过离散傅里叶逆变换在时域中重建，如公式(7)

21、

22、其中，代表离散傅里叶拟变换，fi′(t)代表f′(t)的第i维，fi'(t)代表在时域中重建的数据的第i维；进而，样本的所有维度均在时域重建，表示为公式(8)：

23、

24、其中，f′(t)表示在时域中重建的数据矩阵，x′(t)代表t时刻经过傅里叶特征滤波器去噪后的样本；

25、步骤1.5：将f′(t)进行特征映射，建立n组特征节点，如公式(9)：

26、

27、其中，zj表示第j组特征节点，n代表特征节点组数；φ为特征映射函数，和是随机生成的特征层的权重与偏置；进而基于傅里叶滤波器的特征层总输出即总特征节点zn可表示为zn≡[z1,z2…,zn]；

28、步骤2：建立门控注意力增强层；

29、步骤2.1：通过映射特征节点zn获得v组增强节点，如公式(10):

30、

31、其中，hu表示第u组增强节点，v代表增强节点组数，ξ为激活函数tanh函数，和是随机生成的增强层的权重和偏置；

32、步骤2.2：定义门控注意力函数waga为公式(11)：

33、

34、其中，τ代表归一化函数，dct代表离散余弦变换，γ是用于调整衰减速率的参数；

35、步骤2.3：定义第u组门控增强节点hu'为公式(12)：

36、hu'＝waga·hu,u＝1,2,…,v (12)

37、定义门控注意力增强层总输出即全部门控增强节点为hv≡[h′1,h′2…,h′v]；

38、步骤3：建立输出层；

39、步骤3.1：将基于傅里叶滤波器的特征层zn与门控注意力增强层hv连接形成新的状态矩阵

40、

41、步骤3.2：利用岭回归训练获得状态矩阵与输出层之间的连接权重

42、步骤3.2.1：输入标签向量y，定义平滑后的标签向量y′如公式(14)：

43、

44、其中，α是标签平滑参数，取值范围为(0,1)；yi,j'和yi,j分别代表平滑后标签y′与原始标签向量y的第i行第j列元素；

45、步骤3.2.2：构建目标函数如公式(15)：

46、

47、其中，第一项为正则化项，λ是正则化参数，取值范围是[10-10,10-1]；第二项为最小二乘误差项；

48、步骤3.2.3：通过令公式(15)关于的导数等于0，可求解出最优连接权重为公式(16)：

49、

50、其中，i是单位矩阵；状态矩阵的穆斯-彭罗斯广义拟矩阵为：

51、

52、因此，

53、步骤3.2.4：获得t时刻的网络输出标签s(t)：

54、

55、其中，m代表样本维度；

56、步骤3.2.5：储存每个滑动窗口内的权重参数

57、步骤4：在线测试；

58、步骤4.1：利用滑动窗口依次输入测试样本，计算各窗口内测试样本与训练样本的余弦相似度，使用相似度最大的训练样本对应的权重参数进行测试；

59、步骤4.2：重复步骤4.1直至滑动所有测试样本，得到网络输出标签，如果标签为0代表无传感器故障，1代表第1个传感器故障，以此类推，初步完成故障诊断；

60、步骤5：当初步诊断精度不满足需求时，添加d个额外增强节点进行增量学习训练，d代表额外增强节点数量，试凑法择优选取任意正整数；

61、步骤5.1：定义额外增强节点hν+1为：

62、

63、其中，ξ为激活函数tanh函数，和是随机设置的权重和偏置；

64、步骤5.2：重复步骤2.2至2.3获得额外门控增强节点hν+1'；

65、步骤5.3：将状态矩阵与额外门控增强节点hν+1'相连接，得到新的拓展状态矩阵如公式(20)：

66、

67、步骤5.4：根据greville定理计算新的连接权重如公式(21)：

68、

69、其中，变换矩阵bt、差值项c、投影项d依次定义为：

70、

71、其中，c+和分别代表差值项c和状态矩阵的伪逆；

72、步骤5.5：获得网络输出标签：

73、

74、其中，m代表样本维度；

75、步骤5.6：储存增量学习后每个滑动窗口内的权重参数

76、步骤5.7：计算增量学习训练精度；

77、步骤5.8：重复步骤5.1至5.7，直至训练精度下降或保持不变；

78、步骤6：增量学习测试；

79、步骤6.1：利用滑动窗口依次输入测试样本，使用增量更新后的权重参数进行测试；

80、步骤6.2：得到网络输出标签，如果标签为0代表无传感器故障，1代表第1个传感器故障，以此类推；

81、步骤6.3：计算故障诊断精度，完成故障诊断；上述步骤中的滑动窗口大小t0，滤波率η，用于调整衰减速率的参数υ，标签平滑参数α，正则化参数λ可通过在取值范围内网格搜索，选择故障诊断精度最高的相应参数而确定。

82、本发明与现有技术相比，具有以下明显的优势和有益效果：

83、本发明利用傅里叶滤波器，衰减低频信号，剔除高频噪声信号，从频域角度提高模型鲁棒性。其次，针对漂移故障初期特性设计门控注意力增强层，从时域角度提高初期故障的可检测性。此外，标签平滑机制可以有效防止模型过拟合，提高模型分类性能。最后，通过动态增强节点，实现模型结构在线调整，提高模型诊断性能。因此，本发明具有对噪声具有鲁棒性、诊断精度高、可适应动态过程、学习速度快及可解释性强等技术优势。