最优控制快速搜索的行星着陆制导方法

本发明涉及一种航天器制导方法，尤其涉及最优控制快速搜索的行星着陆制导方法，属于航天器制导与控制。

背景技术：

1、行星探测是人类认知宇宙规律、实现地外生存的重要手段。行星表面精确着陆技术是行星探测活动的关键技术，也是开展地外天体表面原位探测、采样返回等任务的前提条件。动力下降段是行星表面着陆的关键阶段，关系到着陆器能否安全、精确地到达期望的着陆点。动力下降段的轨迹需要满足多种约束，包括着陆点处的位置和速度等约束，以及着陆过程中的推力幅值和方向约束。此外，着陆器有限的燃耗与星载计算资源也为行星着陆制导方法的设计带来了工程实际的约束。因此，为实现行星表面精确着陆，需要发展能满足多约束条件的着陆制导方法。

2、针对行星着陆制导方法设计已有相关研究，主要包含基于标称轨迹的跟踪制导方法和无标称轨迹的显式制导方法。其中，基于标称轨迹的跟踪制导方法能处理多种约束，但轨迹一般提前设计，故该方法对任务初始偏差的适应性较差；无标称轨迹的显式制导方法对初始条件偏差具有较好的适应性，但难以有效地处理复杂约束。模型预测控制结合上述二者特点，具有应对初始条件偏差和处理复杂约束的能力。其基本思想是，在线滚动求解有限时域内的最优控制问题。由于需要在线求解复杂优化问题，模型预测控制无法保证能满足着陆制导的实时性需求。因此，面向行星表面安全、精确着陆制导需求，有必要对传统的行星着陆制导方法进行改进，发展一种能够处理复杂约束并具有较高实时性的行星着陆制导方法。

技术实现思路

1、针对行星动力下降段中处理复杂约束和满足实时性需求之间的矛盾，从满足着陆器精准着陆、降低燃耗的需求出发，本发明主要目的是提供最优控制快速搜索的行星着陆制导方法，将着陆器动力学模型解耦为有控动力学模型和无控动力学模型，求解一个预测时域内有控运动的可达区，离线获得着陆器抵达可达区内不同位置的燃耗最优控制，并将最优控制与着陆器末状态分别存储为最优控制数据库和终点状态数据库。在着陆过程中将无控运动与终点状态数据库进行叠加，得到着陆器的状态预测空间，搜索最优终端状态，得到最优控制数据库中对应的最优控制指令，根据最优控制指令实现行星着陆制导。

2、本发明的目的是通过下述技术方案实现的。

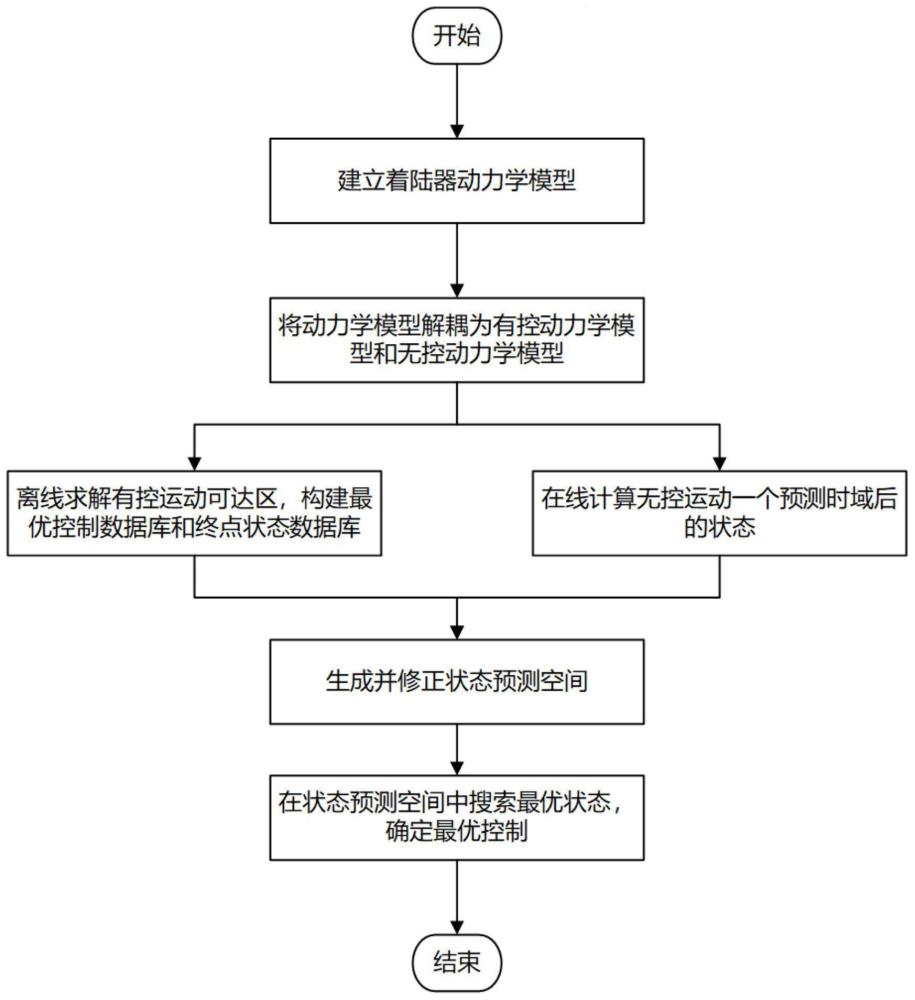
3、本发明公开的最优控制快速搜索的行星着陆制导方法，包括如下步骤：

4、步骤一、在行星着陆点固连坐标系下，建立着陆器动力学模型，并将着陆器动力学模型解耦为有控动力学模型和无控动力学模型，其中，有控动力学模型对应着陆器在仅受推力时的运动，无控动力学模型对应着陆器在仅受引力时的运动。

5、步骤一的具体实现方法为：

6、定义着陆点固连坐标系o-xyz：以着陆点为坐标系原点o，ox轴指向当地的东向，oy轴指向当地的北向，oz轴指向当地的天顶方向。

7、忽略行星自转和气动力的影响，并将行星重力加速度视作常数，在着陆点固连坐标系下建立着陆器动力学模型：

8、

9、式中，r和v分别表示着陆点固连坐标系下着陆器的位置矢量和速度矢量，a表示着陆器的推力加速度矢量，t表示着陆器的推力矢量，m表示着陆器质量，g表示行星表面重力加速度矢量，isp表示着陆器发动机比冲，g0表示地球海平面重力加速度的数值。

10、根据运动独立性原理，着陆器的运动可看作分别由推力和重力驱动的两个分运动的合成，两个分运动独立进行，互不干扰。对式(1)中位置和速度方程积分可得：

11、

12、式中，t表示运动时间，r0和v0分别表示初始时刻的位置矢量和速度矢量。

13、通过分析如式(2)所示的位置和速度方程将动力学方程解耦为有控动力学模型和无控动力学模型，分别如式(3)和式(4)所示：

14、

15、

16、有控动力学模型中，着陆器初始位置和速度均为0，只受推力作用；无控动力学模型中，着陆器初始位置和速度分别为r0和v0，只受重力作用。

17、步骤二、设定预测时域，根据步骤一中的有控动力学模型，以推力幅值约束和推力方向约束为约束条件构建可达区的优化模型，根据优化模型求解一个预测时域内的有控运动可达区；以可达区内不同位置为虚拟终点，以燃耗为优化目标，以推力幅值约束和推力方向约束为约束条件，构建燃耗优化模型，根据燃耗优化模型离线优化获得着陆器抵达指定虚拟终点位置的燃耗最优控制，并将最优控制存储为最优控制数据库，将对应的虚拟终点状态存储为终点状态数据库。

18、步骤二的具体实现方法为：

19、着陆器受到的控制约束包括推力幅值约束和推力方向约束，如式(5)所示：

20、

21、式中，tmin和tmax分别表示推力幅值的最小值和最大值，nz表示z轴正向的单位向量，θmax表示发动机摆角最大值，其定义为推力矢量与z轴正方向的最大夹角。

22、设定预测时域为tn。离线求解一个预测时域内的有控运动可达区。考虑推力关于z轴的旋转对称性，可先求解着陆器在xoz第一象限的二维可达区，再绕z轴旋转一周即可得到三维可达区。根据步骤一中的有控动力学模型，以推力幅值约束和推力方向约束为约束条件构建二维可达区的优化模型，如式(6)所示：

23、

24、式中，所有矢量均为二维向量，xi和zi分别表示着陆器可抵达的x轴和z轴坐标，选取不同的zi，优化得到此时着陆器能抵达的最远x轴位置xi，坐标(xi,zi)形成的包络即为二维可达区，绕z轴旋转即可得到三维可达区。

25、在可达区内选取不同位置ri为虚拟终点，以燃耗最优为优化目标，以如式(5)所示的推力幅值约束和推力方向约束为约束条件，建立如式(7)所示的优化模型，根据如式(7)所示的优化模型离线优化获得着陆器抵达指定虚拟终点位置的燃耗最优控制。

26、

27、式中，m0表示初始时刻着陆器的质量。

28、将所有的虚拟终点位置ri、着陆器抵达ri时的vi、着陆器的燃耗δm存储为终点状态数据库，对应的最优控制加速度ai存储为最优控制数据库，为便于存储，将最优控制加速度ai离散为最优控制加速度序列ai,j进行存储，其中j＝1,2,…,tn/tg，tg表示制导周期，tn是tg的整数倍。

29、步骤三、在着陆过程中，根据无控动力学模型计算着陆器经历一个预测时域无控运动后的状态，将无控运动末状态与步骤二得到的终点状态数据库进行叠加，生成着陆器在一个预测时域内的状态预测空间；将状态预测空间中因质量变化导致违反控制约束的状态点剔除；将一个预测时域内的着陆器质量近似等效为常数，根据当前时刻着陆器的质量与初始时刻的质量之比构建燃耗修正因子α，并根据燃耗修正因子α修正燃耗；在状态预测空间遍历搜索最优状态，得到最优控制数据库中对应的最优控制指令，根据最优控制指令实现行星着陆制导。

30、步骤三的具体实现方法为：

31、在着陆过程的t时刻，根据无控动力学模型，计算着陆器经历一个预测时域无控运动后的状态，如式(8)所示：

32、

33、式中，ru、vu和mu分别表示经过一个预测时域无控运动后着陆器的位置矢量、速度矢量和质量。

34、将无控运动的末状态与终点状态数据库中的有控运动末状态进行叠加，生成t时刻着陆器在一个预测时域内的状态预测空间xn，如式(9)所示：

35、xn＝{(rn,vn,mn)|rn＝ru+ri,vn＝vu+vi,mn＝mu-δmi,i＝1,2,...,n} (9)

36、式中，rn、vn和mn分别表示经过一个预测时域后着陆器的位置矢量、速度矢量和质量，n表示终点状态数据库中有控运动末状态的数量。

37、考虑到式(7)中着陆器的初始质量取为m0，最优控制数据库中的变量为加速度a，故当t时刻着陆器质量减小至m(t)时，最优控制数据库中部分满足推力幅值下限约束的最优控制加速度ae此时不再满足该约束条件，也即：

38、

39、对于ae，要将着陆器状态预测空间xn中对应的状态点xe予以剔除，保证最优控制满足推力约束，此时状态预测空间x如式(11)所示：

40、x＝xn-xe (11)

41、在着陆过程中，着陆器质量的变化率与推力幅值成正比，而推力幅值与着陆器质量成正比。故着陆器质量的变化也会影响状态预测空间x中燃耗的值。将一个预测时域内的着陆器质量近似等效为常数，根据当前时刻着陆器质量与初始时刻质量之比构建燃耗修正因子α如式(12)所示：

42、

43、在着陆过程的t时刻，选取如式(13)-(15)所示的性能指标：

44、

45、

46、

47、式中，λ<0表示燃耗权重系数，k表示速度权重系数，rx、ry和rz分别表示当前时刻着陆器三轴位置，vx、vy和vz分别表示当前时刻着陆器三轴速度，tgo表示着陆器剩余飞行时间，d>0是防止q发生奇异的常数。

48、根据式(13)至(15)所示性能指标，在着陆器状态预测空间x中遍历搜索最优状态x*，以最优状态x*在最优控制数据库中对应的最优控制序列ai,j的第一项ai,1为实际最优控制，驱动着陆器向目标点运动。

49、在每个制导周期均执行一次上述的终端状态预测和最优控制搜索，根据搜索得到的最优控制指令进行行星着陆制导，直至着陆器抵达目标着陆点。

50、有益效果：

51、1、针对行星着陆存在推力幅值约束和方向约束等多种约束的问题，本发明公开的最优控制快速搜索的行星着陆制导方法，离线计算着陆器可达区，并在可达区范围内求解满足推力约束的燃耗最优控制，将其存储于最优控制数据库中，在线搜索最优控制，保证搜索得到的控制量均满足约束条件。在着陆过程中根据着陆器质量变化动态调整最优控制搜索范围，修正燃耗数据，进一步保证了不违背控制约束条件进行行星着陆制导。本发明制导方法离线求解满足约束条件的最优控制，并在线修正数据，能够保证满足着陆器的控制约束。

52、2、针对行星着陆器计算机的计算和存储能力有限等工程现实约束条件，本发明公开的最优控制快速搜索的行星着陆制导方法，将着陆器的动力学模型解耦为有控动力学模型和无控动力学模型，并在终点状态数据库中仅存储有控运动相关的数据，减小了星载计算机的数据存储量和在线搜索的计算量；以可达区内不同位置为虚拟终点，以燃耗为优化目标，以推力幅值约束和推力方向约束为约束条件，构建燃耗最优控制优化模型，根据燃耗优化模型离线求解优化问题，在着陆过程中仅需调用两个数据库并搜索最优控制，无需在线求解优化问题，减小了星载计算机的工作负担。本发明制导方法计算量小，搜索速度快，能够满足星载计算机的计算性能约束。

53、3、本发明公开的最优控制快速搜索的行星着陆制导方法，在实现有益效果1和2的基础上，能够实现燃耗最优条件下的行星着陆制导，同时着陆器的着陆位置精度和速度精度都满足终端约束，能够实现在行星表面精准地着陆。