基于扩张观测器和鸽群优化的高速飞行器动态逆控制方法

本发明涉及高超声速飞行器纵向运动控制领域，尤其是一种具有强鲁棒性的跟踪控制方法，适用于高超声速飞行器在强不确定环境下的跟踪控制。

背景技术：

1、高超声速飞行器纵向运动模型具备强烈的非线性和耦合性，是一个复杂的非线性系统。随着非线性控制理论的发展，基于非线性模型直接设计控制器的方法逐渐发展起来。动态逆作为其中一种典型的设计方法，对于非线性问题来说有着很好的解决能力。此外，由于高超声速飞行器飞行过程中存在各种扰动和气动参数变化，导致无法对其运动模型进行精确建模。对于飞行器模型中的强不确定性问题，扩张状态观测器是一种有效的解决办法。最后，考虑到扩张状态观测器中参数较多，设计依赖工程经验的问题，鸽群优化能够对观测器参数进行最优化，提高控制器跟踪效果。

2、与传统飞行器相比，高超声速飞行器飞行环境复杂、飞行包线跨域大、气动特性变化剧烈、运动模型严重耦合，对于控制系统设计提出了严苛的要求。因此，研究在强不确定环境下的高超声速飞行器纵向运动跟踪控制问题，保证其在飞行过程中控制系统的稳定性和可靠性，具有十分重要的理论意义和工程价值。动态逆控制仅针对精确模型具备良好的控制效果，为了应对飞行器模型的不确定性，设计扩张状态观测器对模型的不确定性进行估计和补偿，再结合动态逆方法，设计飞行器的跟踪控制器，最后，利用鸽群优化算法对观测器模型参数进行优化。该方法在提高姿态控制系统的安全性和可靠性的同时，也使系统的控制精度有所提高。

技术实现思路

1、为了克服现有技术的不足，本发明提供一种基于扩张观测器和鸽群优化的高速飞行器动态逆控制方法。为了解决传统动态逆控制无法适应高超声速飞行器强不确定性的问题，本发明针对高超声速飞行器在强不确定环境和强干扰条件下的纵向运动，提出了一种基于扩张状态观测器和鸽群优化算法的动态逆控制系统设计方法。基于动态逆控制方法，进行控制器设计，再引入扩张状态观测器，对纵向运动模型的不确定性和扰动进行补偿，得到最终的控制输入。最后，引入鸽群优化算法，对扩张状态观测器参数进行优化，提升控制器控制效果。该方法能够在飞行器存在扰动和强不确定的情况下，保证跟踪效果。

2、本发明针对高超声速飞行器飞行过程中气动特性变化剧烈，飞行环境复杂的问题，研究在考虑飞行器模型不确定性和外部扰动情况下，实现高超声速飞行器稳定跟踪指令的方法，并经过仿真验证了方法的有效性。首先，针对高超声速飞行器纵向运动模型，基于动态逆方法，将运动非线性模型解耦为线性状态方程。然后，引入扩张状态观测器，对模型不确定性和外部扰动进行补偿，结合动态逆设计控制器。最后，基于鸽群优化算法优化扩张状态观测器参数，提高控制器的控制效果。

3、本发明解决其技术问题所采用的技术方案的步骤如下：

4、步骤1：首先建立高超声速飞行器的纵向运动模型；

5、高超声速飞行器的纵向运动模型具有强耦合以及严重的非线性特点，如果对其全状态的非线性运动方程进行研究，将会非常困难，这是由于模型的阶次较高，使得系统难以设计，甚至不能够实现。为了便于研究，必须对高超声速飞行器全状态非线性方程进行解耦。当高超声速飞行器在平衡飞行条件下，满足水平无侧滑飞行条件时，高超声速飞行器的运动便可以分解成相互之间不耦合的纵向运动和横向运动。

6、针对纵向运动，纵向运动是高超声速飞行器在基准运动平面内(对称平面内)发生的运动；由于在平衡飞行条件下，水平无侧滑飞行，高超声速飞行器的滚转角φ、侧滑角β、滚转角速度p以及偏航角速度r皆为0，所以通过对高超声速飞行器全状态非线性运动方程简化，得到纵向模型的非线性方程组，如式(1)所示：

7、

8、式中，v为飞行速度，γ为飞行航迹角，q为俯仰角速度，α为飞行迎角，h为飞行高度，m为高超声速飞行器的质量，iy为高超声速飞行器沿y轴的转动惯量，和分别为v，γ，q，α和h的导数，l为升力，d为阻力，t为推力，my为俯仰力矩，表达式如下：

9、

10、其中，ρ为空气密度，s为参考面积，c为高超声速飞行器的平均气动弦长，g为重力加速度，升力系数cl，阻力系数cd，推力系数ct，力矩系数cm(α)、cm(δe)和cm(q)的表达式如下所示：

11、

12、其中，ce为常值系数，δe为升降舵偏角，β为节流阀调定值，节流阀调定值变化遵循如下所示二阶模型：

13、

14、其中，ωn为自然频率，ξ为阻尼比，为β的一阶导数，为β的二阶导数，βc为发动机节流阀调定值的指令信号，通过调节βc的大小控制高超声速飞行器发动机推力的大小，βc越大，二阶模型中的节流阀调定值β就越大，即发动机油门更大，产生的推力就更大；反之，则更小；

15、步骤2：针对纵向运动模型，基于扩张状态观测器和动态逆方法进行控制器设计，具体步骤如下：

16、选择状态量为x＝[vγαβh]t，控制输入为u＝[βcδe]t，并基于李氏求导对式(1)进行线性化，将纵向运动模型解耦为速度子系统和高度子系统；

17、状态方程部分，速度子系统的状态方程如式(6)所示：

18、

19、高度子系统的状态方程如式(7)所示：

20、

21、其中，f1(x)＝(tcosα-d)/m-gsinγ，f2(x)＝vsinγ，f3(x)＝(l+tsinα)/mv-gcosγ/v，和分别表示飞行速度v的二阶导数和三阶导数；和h(4)分别表示飞行高度h的二阶导数，三阶导数和四阶导数；分别表示状态量x的一阶导数，二阶导数和三阶导数；和分别为飞行航迹角γ的二阶导数和三阶导数；

22、控制输入部分，将输入δe和βc从状态方程中解耦出来：

23、

24、其中，表示攻角α的二阶导数，记并取

25、

26、步骤3：基于步骤2的解耦合和线性化，得到如下所示的线性动态方程：

27、

28、其中

29、

30、

31、

32、

33、

34、

35、根据动态逆控制原理，控制输入u由式(17)得出：

36、u＝b+([v1 v2]t-a) (16)

37、其中，b+是矩阵b的广义逆矩阵，v1为速度子系统的控制律，v2为高度子系统的控制律；

38、步骤4：首先，对速度子系统的控制律v1进行设计；从公式(10)得到速度子系统的线性方程为：

39、

40、基于巴特沃斯低通滤波器，设计控制律v1的形式为：

41、

42、其中vc为速度指令；然而，该控制律仅在飞行器运动模型准确、不存在外部扰动的条件下适用；考虑到实际工程中，往往存在模型不确定性和外部扰动，因此，将控制律(19)代入(10)和(17)，得到实际的速度子系统变化为：

43、

44、其中，△1为模型不确定性和外部扰动的总和；

45、步骤5：针对步骤4中描述的模型不确定性和外部扰动对速度子系统的不良影响，设计扩张状态观测器，对模型不确定性和外部扰动进行估计与补偿；将公式(20)重写为：

46、

47、其中xv1＝v，y1表示速度子系统的输出，和分别表示xv1，xv2，xv3和xv4的一阶导数。

48、进而，得到扩张状态观测器的形式为：

49、

50、其中αv1，αv2，αv3，βv1，βv2，βv3，βv4，δv为待设计参数，和分别表示z1v，z2v，z3v和z4v的一阶导数，且fal(e,α,δ)的形式为：

51、

52、选择参数αv1，αv2，αv3，βv1，βv2，βv3和δv，直至系统稳定，且扩张状态观测器(22)能够对状态方程(21)的状态进行估计，即z1v→xv1，z2v→xv2，z3v→xv3，z4v→xv4；

53、步骤6：基于步骤5的扩张状态观测器，z4v对状态方程(21)的状态xv4的真实值进行估计，因此，模型不确定和外部扰动之和△1的值表示为：

54、

55、在考虑模型不确定性和外部扰动的情况下，速度子系统的控制律(19)重写为：

56、

57、将式(24)代入式(25)，得到速度子系统的实际控制律为：

58、

59、在实际控制律的控制下，保证速度子系统在存在模型不确定性和外部扰动的情况下，稳定跟踪速度指令信号；

60、步骤7：从步骤2可知，高超声速飞行器的纵向运动被分为了速度子系统和高度子系统；步骤4-6对速度子系统进行了控制器设计，现在开始对高度子系统进行控制器设计，与步骤4相似，基于巴特沃斯低通滤波器，设计控制律v2的形式为：

61、

62、其中hc为高度指令；由于模型不确定性和外部扰动的存在，将控制律(27)代入(10)和(17)，得到实际高度子系统变化为：

63、h(4)＝v2+△2 (27)

64、其中，△2为模型不确定性和外部扰动的总和；

65、步骤8：公式(28)重写为：

66、

67、其中xh1＝h，xh4＝h(3)，y2表示高度子系统的输出，和分别表示xh1，xh2，xh3，xh4和xh5的一阶导数；进而，得到扩张状态观测器的形式为：

68、

69、其中αh1，αh2，αh3，αh4，βh1，βh2，βh3，βh4，βh5，δh为待设计参数，和分别表示z1h，z2h，z3h，z4h和z5h的一阶导导数；选择设计参数αh1，αh2，αh3，αh4，βh1，βh2，βh3，βh4，βh5，δh，直至系统稳定，且扩张状态观测器式(30)能够对状态方程(29)的状态进行估计，即z1h→xh1，z2h→xh2，z3h→xh3，z4h→xh4，z5h→xh5；

70、步骤9：基于步骤8中的扩张状态观测器公式(30)，z5h对状态方程(30)的状态xh5的真实值进行了估计，因此，模型不确定和外部扰动之和△2的值表示为：

71、

72、在考虑模型不确定性和外部扰动的情况下，高度子系统的控制律(27)重写为：

73、

74、将式(31)代入式(32)，得到高度子系统的实际控制律为：

75、

76、在该控制律的控制下，保证高度子系统在存在模型不确定性和外部扰动的情况下，稳定跟踪高度指令信号；

77、步骤10：初始化pio算法参数，pio算法参数包括解空间的维数dim、种群规模pn、地图因子r、指南针算子最大迭代次数nc1和地标算子最大迭代次数nc2，其中nc1<nc2；求解变量为：

78、z＝[βv1,…,βv4,βh1,…,βh5] (33)

79、步骤11：设置每只鸽子的随机速度和路径；比较每只鸽子的适应度值，找出目前适应度值最小的路径；其中适应度函数为：

80、

81、其中fitness表示适应度值，tf为终端时间，v为飞行速度，vc为速度指令，h为飞行高度，hc为高度指令；

82、步骤12：用zi和vi分别表示第i只鸽子的位置和速度，第i只鸽子的速度和鸽子的位置分别用公式进行相应的迭代计算，其中第i只鸽子的速度更新公式为：

83、vi(k)＝vi(k-1)·e-rk+rand·(zg-zi(k-1)) (35)

84、第i只鸽子的高度更新公式为：

85、zi(k)＝zi(k-1)+zi(k) (36)

86、其中，r是地图因子，rand是一个随机数，为迭代次数，zg为鸽子的最好位置，vi(k)，zi(k)表示第k次迭代的鸽子的速度和鸽子的位置，vi(k-1)，zi(k-1)表示第k-1次迭代的鸽子的速度和鸽子的位置，即能够使式(35)的适应度值最小的变量z；

87、首先，通过使用公式(36)和(37)更新每一个鸽子的速度和路径zi(k-1)和vi(k-1)；然后比较所有鸽子的适应度值，选择能使适应度值最小的zi(k)和vi(k)作为新的最佳路径；

88、步骤13：如果nc>nc1，转到步骤14；否则，转到步骤11，其中，nc为求解过程的迭代次数；

89、步骤14：所有的鸽子根据自身的适应度值按从小到大排名，为减少不良个体对整体优化的不利影响，将排名在后半部分的鸽子去除，即鸽子总数减半，如公式(38)所示：

90、

91、然后，根据公式(39)找到所有鸽子的位置中心zc(k)：

92、

93、位置中心是理想的目的地，所有鸽子的位置更新方向都应该向位置中心靠拢，因此，基于随机梯度下降法，设计式(40)对飞行方向进行调整，从而保证鸽子始终向位置中心靠拢：

94、zi(k)＝zi(k-1)+rand·(zc(k)-zi(k-1)) (39)

95、将中心位置zc(k)存储为最佳的解决方案参数[βv1,…,βv4,βh1,…,βh5]，该参数能够保证状态观测器(22)和(30)对不确定性和扰动的估计效果达到最优，进而提升控制系统性能，同时避免了人为调参的不确定性和随机性，极大提升了控制器设计的效率；

96、其中，np(k)为第k次迭代的鸽子总数，np(k-1)为第k-1次迭代的鸽子总数，zc(k)为第k代所有鸽子的中心位置；

97、步骤15：如果nc>nc2，停止操作，并输出最佳路径结果zc＝[βv1,…,βv4,βh1,…,βh5]作为扩张状态观测器(22)和(30)的参数；如果不满足nc>nc2，转到步骤13。

98、所述发动机模型参数分别选为：

99、

100、所述公式(19)中，取值为av0＝1，av1＝2，av2＝2。

101、所述公式(27)中，取值为ah0＝1，ah1＝2.613，ah2＝3.141，ah3＝2.613。

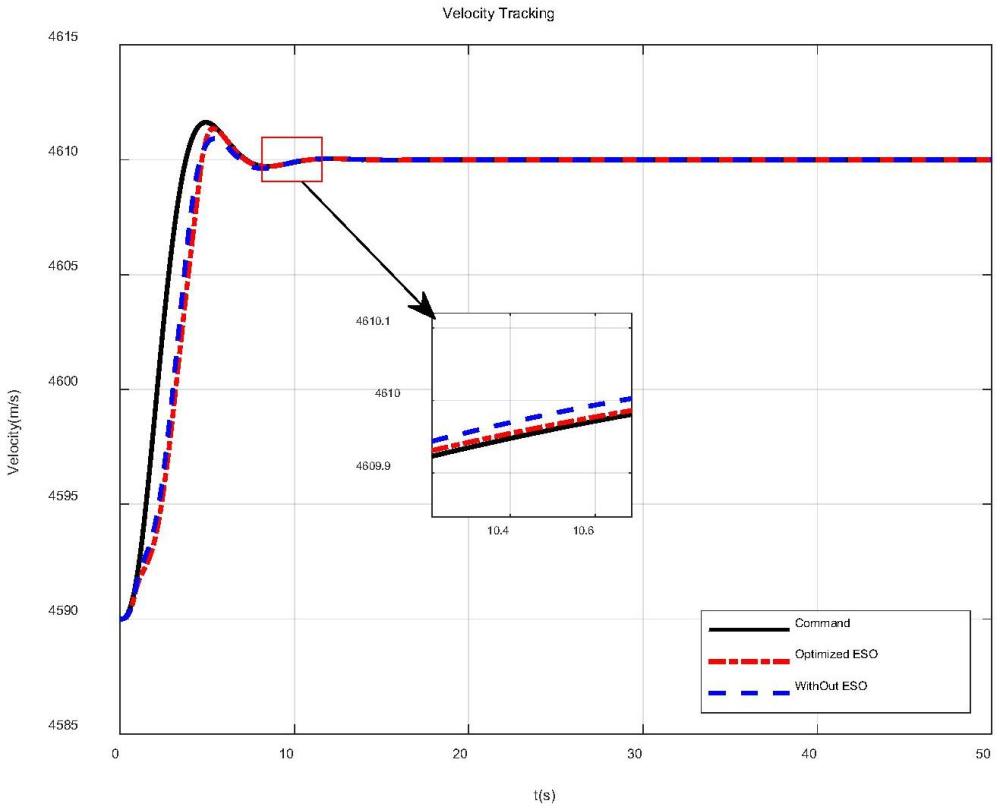
102、本发明的有益效果在于面向高超声速飞行器纵向运动高度和速度跟踪控制，考虑了模型不确定性和外部扰动，设计了基于扩张状态观测器和鸽群优化的动态逆控制器。该控制器能够实现准确跟踪的主要原因是引入了扩张状态观测器，对高超声速飞行器纵向运动模型的不确定性和扰动进行了估计与补偿，反馈到了动态逆控制律设计中，从而抵消了模型不确定性和外部扰动对跟踪控制的不良影响。并基于鸽群优化对扩张状态观测器参数进行了优化，提升了控制效果。如此，准确的高度和速度跟踪得以维持。与传统动态逆方法所设计的控制器进行仿真分析对比，结果表明，本发明所设计的控制器性能优良。