基于CB制导的T-S模糊动态滑模动力定位控制方法

本发明涉及船舶控制，尤其涉及一种基于cb制导的t-s模糊动态滑模动力定位控制方法。

背景技术：

1、在船舶的动力定位技术方面，主要面临的挑战是如何克服外部干扰，使船舶维持在预定的船位。由于船舶在水面行驶时会受到多种力的作用，这使得船舶的定位问题变得更加复杂。即便在关闭推进系统的情况下，船舶仍可能因为水流、风力等的持续作用下而偏离预定的船位。如果完全依赖人工操作来管理推进和转向系统，不仅劳动强度大，还可能因为操作失误而导致船舶失控。

2、尽管目前已有众多学者提出了多种船舶动力定位控制方案，但这些方案仍存在以下问题：

3、现有方案在使用t-s模糊模型对船舶进行模型构建时，忽略了船舶系统中的非线性项和不确定性因素，如复杂气候和极端天气造成的外部干扰，这会导致模型的准确性和鲁棒性下降，控制效果会受到严重影响。

技术实现思路

1、本发明提供一种基于cb制导的t-s模糊动态滑模动力定位控制方法，以克服上述技术问题。

2、为了实现上述目的，本发明的技术方案是：

3、一种基于cb制导的t-s模糊动态滑模动力定位控制方法，包括以下步骤：

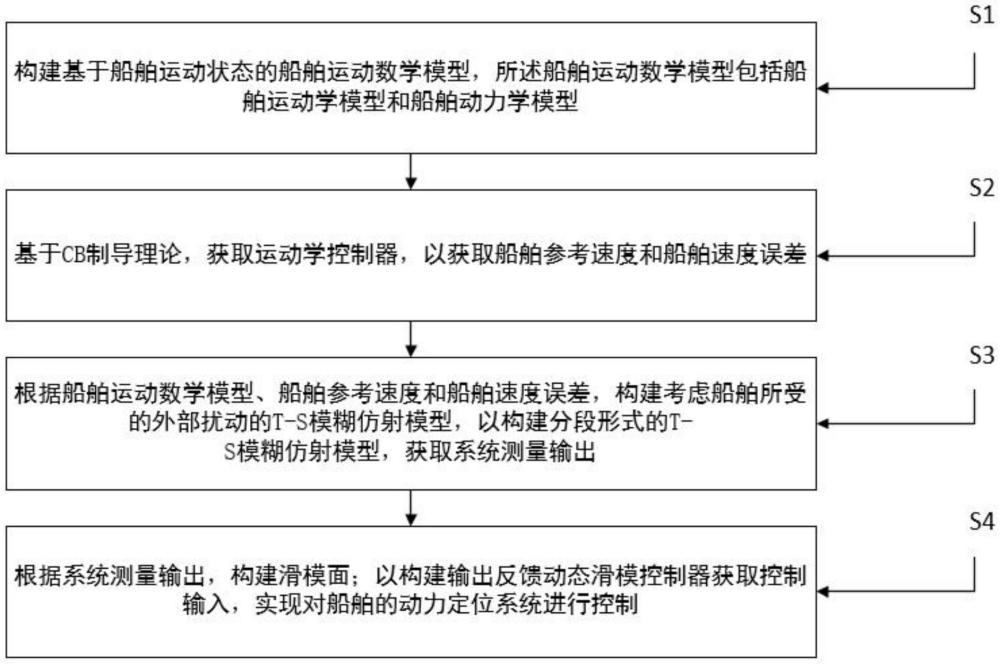
4、s1：构建基于船舶运动状态的船舶运动数学模型，所述船舶运动数学模型包括船舶运动学模型和船舶动力学模型；

5、s2：基于cb制导理论，获取运动学控制器，以获取船舶参考速度和船舶速度误差；

6、s3：根据船舶运动数学模型、船舶参考速度和船舶速度误差，构建考虑船舶所受的外部扰动的t-s模糊仿射模型，以构建分段形式的t-s模糊仿射模型，获取系统测量输出；

7、s4：根据系统测量输出，构建滑模面；以构建输出反馈动态滑模控制器，获取控制输入，实现对船舶的动力定位系统进行控制。

8、进一步的，所述s2中，获取船舶参考速度和船舶速度误差的方法如下：

9、s211：基于cb制导理论，获取船舶的实际位置和姿态与船舶的期望位置和姿态之间的误差向量如下：

10、

11、其中，qη为船舶的实际位置和姿态与船舶的期望位置和姿态之间的误差向量，η为船舶的实际位置和姿态，ηd为船舶的期望位置和姿态，表示定义为；

12、s212：根据船舶的实际位置和姿态与船舶的期望位置和姿态之间的误差向量，构建制导率，以获取船舶参考速度：

13、s213：根据所述船舶参考速度，获取船舶速度误差。

14、进一步的，所述s212中，所述船舶参考速度获取如下：

15、

16、其中，xd(t)为船舶参考速度，为r(·)的转置，r(·)为变换矩阵，为ηd的一阶导数，uc,max为设定的参数矩阵，△为设定的参数，为qη的转置。

17、进一步的，所述s213中，所述船舶速度误差获取如下：

18、xe(t)＝x(t)-xd(t)

19、其中，

20、式中：xe(t)为船舶速度误差，x(t)为船舶实际速度，xd(t)为船舶参考速度，为xe(t)的一阶导数，为x(t)的一阶导数，为xd(t)的一阶导数。

21、进一步的，所述s3中，所述分段形式的t-s模糊仿射模型构建如下：

22、首先，构建t-s模糊仿射模型如下：

23、

24、其中，u(t)为船舶的纵荡速度，为第l个模糊推理规则下的u(t)的模糊集，ν(t)为船舶的横荡速度，为第l个模糊推理规则下的ν(t)的模糊集，r(t)为船舶的艏向角速度，为第l个模糊推理规则下的r(t)的模糊集，为xe(t)的一阶导数，xe(t)为船舶速度误差，pl为第l个模糊推理规则下的仿射模型状态参数矩阵，δpl为pl的不确定项，xd(t)为船舶参考速度，xl为第l个模糊推理规则下的仿射模型仿射项，δxl为xl的不确定项，ql为第l个模糊推理规则下的仿射模型控制输入参数矩阵，δql为ql的不确定项，τ(t)为控制输入，ol为第l个模糊推理规则下的仿射模型外部扰动参数矩阵，ω(t)为外部扰动，y(t)为系统测量输出，s为仿射模型控制输出状态参数矩阵，z(t)为调节输出，hl为第l个模糊推理规则下的仿射模型调节输出状态参数矩阵，nl为第l个模糊推理规则下的仿射模型调节输出输入状态参数矩阵，l为模糊推理规则的索引值，为模糊推理规则的索引值的集合，n为模糊推理规则的索引值的总数；

25、于是，所述分段形式的t-s模糊仿射模型构建如下：

26、

27、式中：为xe(t)的一阶导数，xe(t)为船舶速度误差，pi为前提变量第i个空间分区的分段仿射模型状态参数矩阵，δpi为pi的不确定项，xd(t)为船舶参考速度，xi为前提变量第i个空间分区的分段仿射模型仿射项，δxi为xi的不确定项，qi为前提变量第i个空间分区的分段仿射模型控制输入参数矩阵，δqi为qi的不确定项，oi为前提变量第i个空间分区的分段仿射模型外部扰动参数矩阵，hi为前提变量第i个空间分区的分段模型调节输出状态参数矩阵，ni为前提变量第i个空间分区的分段仿射模型调节输出输入状态参数矩阵，u(t)为船舶的纵荡速度，si为第i个前提变量空间分区；i为前提变量空间分区的索引值，i＝i0∪i1为区域索引的集合，其中，i0为包含原点的区域索引的集合，i1为不包含原点的区域索引的集合；τ(t)为控制输入，y(t)为系统测量输出，s为仿射模型控制输出状态参数矩阵，z(t)为调节输出，ω(t)为外部扰动；

28、其中：

29、

30、其中，

31、式中：m为仿射模型的索引值，为前提变量第i个空间分区的si中的插值内使用的局部模型的索引，：＝表示相当于，μm为第m个仿射模型的隶属度值，pm为第m个仿射模型状态参数矩阵，δpm为pm的不确定项，xm为第m个仿射模型仿射项，δxm为xm的不确定项，qm为第m个仿射模型控制输入参数矩阵，δqm为qm的不确定项，om为第m个仿射模型外部扰动参数矩阵，hm为第m个仿射模型调节输出状态参数矩阵，nm为第m个仿射模型调节输出输入状态参数矩阵，μm[u(t)]为第m个仿射模型的u(t)的隶属度值。

32、进一步的，所述s4中，所述滑模面构建如下：

33、s(t)＝ky(t)+τ(t)＝0

34、其中，s(t)为滑模面，k为滑模面增益，y(t)为系统测量输出，τ(t)为控制输入。

35、进一步的，所述s4中，所述输出反馈动态滑模控制器构建如下：

36、

37、其中，为τ(t)的一阶导数，τ(t)为控制输入，ρ>0为给定标量，ζ(t)为中间计算参数，sgn(s(t))为s(t)的符号函数，s(t)为滑模面，m为仿射模型的索引值，m∈m，m为全部的仿射模型的索引值的集合，n1为仿射模型的索引值的总数，μm为第m个仿射模型的隶属度值，qm为第m个仿射模型控制输入参数矩阵，k为滑模面增益，滑动面区域设为其中，ω为滑动面区域，xe(t)为船舶速度误差，为与xe(t)相关的n1维实数空间，||xe(t)||为xe(t)的绝对值，σ为非负的常数。

38、进一步的，所述s1中，所述船舶运动学模型构建如下：

39、

40、式中，为η(t)的一阶导数，η(t)＝[χ(t)λ(t)ψ(t)]t为船舶在世界坐标下的状态向量，χ(t)为船舶的横坐标，λ(t)为船舶的纵坐标，ψ(t)为船舶的艏向角，r(ψ(t))为ψ(t)的旋转矩阵，x(t)为船舶在船体坐标下的三维速度向量；

41、其中，所述船舶动力学模型构建如下：

42、

43、式中，m为惯性矩阵，x(t)＝[u(t)v(t)r(t)]t为船舶实际速度，u(t)为船舶的纵荡速度，v(t)为船舶的横荡速度，r(t)为船舶的艏向角速度，为x(t)的一阶导数，cm(x(t))为x(t)的科里奥利力和向心力矩阵，gm(x(t))为x(t)的非线性阻尼矩阵，τ(t)＝[τ1(t)τ2(t)τ3(t)]t为控制输入，τ1(t)为纵向输入力矩，τ2(t)为横向输入力矩，τ3(t)为偏航力矩，ω(t)为外部扰动；

44、所述船舶运动数学模型如下：

45、x(t)＝px(t)+qτ(t)+oω(t)

46、式中，p、q和o均为中间计算参数，其中，p＝-m-1(cm(x(t))+gm(x(t)))，q＝o＝m-1，m为惯性矩阵，m-1为m的逆矩阵，cm(x(t))为x(t)的科里奥利力和向心力矩阵，gm(x(t))为x(t)的非线性阻尼矩阵，x(t)为船舶实际速度，τ(t)为控制输入，ω(t)为外部扰动。

47、有益效果：

48、本发明的一种基于cb制导的t-s模糊动态滑模船舶动力定位控制方法，根据船舶运动数学模型、船舶参考速度和船舶速度误差，构建考虑船舶所受的外部扰动的t-s模糊仿射模型，船舶所受的外部扰动包括复杂气流和极端天气带来的外部扰动，使得本发明提供的t-s模糊仿射模型具有较高的准确性和鲁棒性，基于本发明提供的t-s模糊仿射模型的控制效果更好；本发明还将cb制导理论与t-s模糊仿射模型相结合，cb制导理论是一种基于视觉或雷达等传感器信息的导航方法，能够实时获取环境信息，实现目标位置的精确计算，结合本发明提供的t-s模糊仿射模型，能够在不确定和复杂环境下实现更准确的定位。