一种基于神经网络和抗死区函数的磁控形状记忆合金执行器模型预测控制方法

本发明涉及控制工程，尤其是涉及一种基于神经网络和抗死区函数的磁控形状记忆合金执行器模型预测控制方法。

背景技术：

1、磁控形状记忆合金执行器是一种智能材料驱动的微纳米尺度执行器，具备行程大，分辨率高的优点，被广泛应用于精密定位和控制。然而，磁控形状记忆合金中存在固有的率相关、负载相关的非对称迟滞非线性特性，且磁控系统记忆合金的迟滞非线性特性易受温度影响，存在死区现象，严重影响了系统其定位精度，甚至导致系统振荡、不稳定。因此，为了保证磁控形状记忆合金执行器的高精度控制，对其进行建模和高精度控制算法设计具有重要意义。

2、目前描述迟滞非线性系统的模型主要是算子类迟滞模型和微分方程类迟滞模型。其中算子类迟滞模型主要通过不同权值的算子进行叠加来描述迟滞非线性特性，典型的有pi迟滞模型和模型。然而，算子类迟滞模型在描述复杂迟滞非线性特性时，不可避免的存在计算复杂度和建模精度的权衡问题。微分方程类迟滞模型，例如bouc-wen模型、duhem模型等，在描述复杂迟滞非线性特性时精度有限，难以描述磁控形状合金执行器复杂的迟滞非线性特性。因此，设计高性能的迟滞模型来描述磁控形状记忆合金执行器的复杂非线性特性是有必要的。

3、模型预测控制具备概念直观，动态性能好的优点。但是现有的基于线性模型的模型预测控制应用于非线性系统时性能欠佳。此外，现有的模型预测控制在考虑系统死区时，一般基于死区的数学表达式其写成输入约束或者电压矩阵来处理。然后，磁控形状记忆合金执行器中的死区特性伴随在迟滞中，无法获得其数学表达式，现有的考虑死区的模型预测控制算法难以直接应用于磁控形状记忆合金执行器。

4、因此，设计磁控形状记忆合金执行器复杂迟滞非线性特性的高性能迟滞模型，并基于构建的非线性迟滞模型设计考虑死区的模型预测控算法来实现磁控形状记忆合金执行器的高精度控制具有重要研究意义。

技术实现思路

1、本发明主要是解决现有磁控形状记忆合金执行器中建模和控制中的难点，构建高精度的神经网络迟滞模型，并设计带有抗死区函数的神经网络模型预测控制方法来实现磁控形状记忆合金执行器的高精度控制。

2、本发明所采用技术方案如下：

3、一种基于神经网络和抗死区函数的磁控形状记忆合金执行器模型预测控制方法，具体步骤如下：

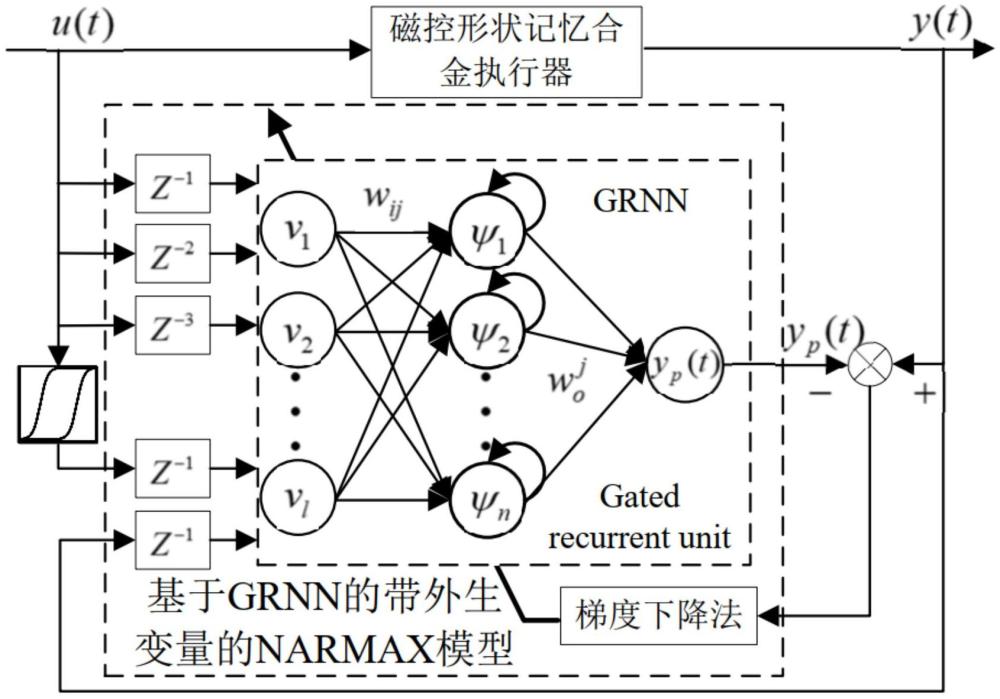
4、步骤1：提出以广义play算子作为外生输入变量的narmax模型，用于描述磁控形状记忆合金执行器的输入输出特性。

5、步骤2：利用门递归神经网络(grnn)逼近narmax模型中的未知函数f，从而得到高精度的基于grnn的narmax的迟滞模型。

6、步骤3：基于构建的神经网络迟滞模型，对系统未来时刻的输出进行预测，从而构建损失函数。并在损失函数中引入设计的抗死区函数。

7、步骤4：最小化构建的损失函数，得到相应的最优控制序列。根据滚动优化原则，将最优控制序列的第一个控制信号应用于系统，实现磁控形状记忆合金执行器的高精度控制。

8、步骤1的具体过程为：

9、带有外生变量广义play算子的namrmax模型表达式如下：

10、

11、其中t为系统采样时刻，f为narmax模型中的未知函数，yp(t)为模型的输出值，y(t-1)为系统在t-1采样时刻的输出，u(t-1)为t-1采样时刻的输入，h(t-1)为外生变量广义play算子的输入。ρ，和χ为输入信号的记忆延时，且设置参数定义为narmax模型的输入矩阵。外生变量广义play算子的数学表达式如下：

12、

13、其中λ，β，δ，是广义play算子中的参数，能够决定play算子的输入输出曲线形状。

14、步骤2的具体过程为：

15、考虑到所提出narmax模型中函数f的表达式难以获得，利用门递归神经网络(grnn)进行逼近，从而得到高精度的基于grnn的narmax的迟滞模型。基于grnn的narmax模型描述如下

16、

17、其中fgrnn(·)表示grnn拟合得到的函数。grnn的数学表达式如下：

18、

19、其中，wij是输入层第i个神经元φj(t)的权值，l代表了输入层神经元的个数；yj(t)是隐含层第j个神经元；φj(t)是第j个隐含层神经元yj(t)的输入，n代表了隐含层神经元的个数，φj(t)是隐含层神经元的更新门，θj(t)是隐含层神经元的重置门，σ代表激活函数，是重置门权值，是重置门偏置，是更新门权值，是更新门偏置；是候选隐藏状态，tanh代表激活函数，是候选隐藏状态计算权值，是候选隐藏状态偏置；yp(t)是grnn的输出，是求和层权值；

20、为神经网络中的权值和偏置，定义权值和偏置更新公式如下：

21、

22、

23、其中η是学习因子，α为动量因子。jp为神经网络参数更新过程中的损失函数。

24、步骤3的具体过程为：

25、基于构建的神经网络narmax模型，对系统未来时刻输出预测如下：

26、

27、

28、定义模型预测控制算法中的损失函数如下：

29、

30、其中yd(t)＝[yd(t+1),…,yd(t+hp)]t，δu(t)＝[δu(t),…,δu(t+hc-1)]t，hp和hc表示预测域和控制域，yd(t)为期望轨迹，表示预测输出。θ1和θ2为损失函数的权值因子，通过调节θ2能够调整系统的响应速度，减小抖震。但是，过大的θ2也会使得系统响应速度变慢。针对存在死区的复杂非线性系统，固定的权值系数难以满足性能需求。因此，设计了抗死区函数来动态调节θ2，使得系统在死区阶段能够快速响应，以降低死区对系统性能的负面影响。

31、在模型预测控制中引入抗死区函数，降低死区对系统性能的影响。抗死区函数定义如下：

32、

33、其中e＝yd-y表示跟踪误差；θ0为权值系数θ2的初值；χ1>0，χ2>0表示函数的灵敏度；b1>0，b2>0表示函数的阈值。

34、步骤4的具体过程如下：

35、利用梯度下降法最小化引入死区函数之后的损失函数，根据滚动优化原则求解最优控制序列。控制序列更新公式如下：

36、

37、

38、其中为雅可比矩阵，表达式如下：

39、

40、其中ηc为滚动优化过程中的学习率。u(t+1)为得到的最优控制序列，根据滚动优化原则，将最优控制序列的第一个信号应用于系统，实现磁控形状记忆合金执行器的高精度控制。

41、相关参数按照以下原则进行选取：

42、在基于grnn的narmax模型中，考虑到模型精度和建模复杂度的权衡，输入信号的延时选择为ρ＝1，和χ＝3。则神经网络的输入信号为v＝[y(t-1),h(t-1),u(t-1),u(t-2),u(t-3)]。输入神经元和隐含层神经元个数设置为l＝n＝5。模型中外生变量play算子中参数设置为λ＝4，β＝4.2，δ＝2.5，学习率和动量因子设置为η＝0.65，α＝0.52。在设计的控制算法中参数设置为hp＝hc＝5，学习率ηc＝0.003，θ1＝18，θ0＝400，b1＝0.2，b2＝0.2。

43、本发明的有益效果为：

44、本发明的方法考虑了磁控形状记忆合金执行器的率相关、负载相关且存在死区现象的复杂迟滞非线性特性，提出了一种基于神经网络和抗死区函数的模型预测控制方法，以提升磁控形状记忆合金执行器的控制精度。该方法主要有以下三个优点：一是本发明中提出了一种基于grnn的narmax模型，能够高精度的描述磁控形状记忆合金执行器的复杂迟滞非线性特性。在提出的模型中，引入了广义play算子作为外生变量，打破了常规narmax模型难以直接描述迟滞非线性多值映射现象的限制。此外，grnn是一种高性能的递归神经网络，其递归单元中的更新门和重置门使得其能够存储和遗忘之前的信息，使得grnn能够克梯度消失或梯度爆炸问题，且具备较强的泛化性能。因此，相较于一般的迟滞模型，所提出模型具备更高的精度和泛化性。二是本发明中利用构建的基于grnn的narmax模型对磁控形状记忆合金执行器的输入输出特性进行预测，设计了基于神经网络的模型预测控制算法。相较于常规的基于线性模型设计的模型预测控制算法，所提出方法精度更高，更适合应用于带有复杂迟滞非线性的磁控形状记忆合金执行器的控制。三是在本发明中针对磁控形状记忆合金执行器中的死区特性，在控制算法中引入了抗死区函数。区别于一般的模型预测控制中将死区转换为死区矩阵或不等式约束的形式，本发明中提出的抗死区函数不依赖死区的数学表达式，能够处理广义的死区现象，提升了所设计控制算法应用于工程实践的潜力。

45、本发明的方法充分考虑了磁控形状记忆合金执行器的率相关、负载相关且存在死区现象的复杂迟滞非线性特性，提升了磁控形状记忆合金执行器的高精度控制，促进了其实际工程应用。