弹簧和惯容器支撑的隔振器及隔振器固有频率调整方法

本发明属于隔振器，具体涉及一种弹簧和惯容器支撑的隔振器及隔振器固有频率调整方法。

背景技术：

1、设有弹性梁的隔振器作为一种基本结构单元有着广泛的应用，在建筑、航空、航天、船舶等工程领域都是必不可少的存在，这些结构总是受到各种外部激励的影响而产生复杂的振动，如果不对其实施有效的控制，系统的结构稳定性和工作精度可能会因为振动带来巨大的影响，从而造成机械精密结构损坏、精度下降、指标漂移等问题。

2、现有方案一般是在弹性梁的边界上加装准零刚度弹簧来提高负刚度，从而减小固有频率。准零刚度弹簧是由一个垂向弹簧(一般为结构自身弹性)和两个预压缩的横向弹簧组成，垂向弹簧提供正刚度，两个预压缩的横向弹簧会在垂直方向上产生负刚度，从而降低弹性梁的固有频率。这种方法存在以下问题：

3、1、准零刚度弹簧中的两个预压缩的横向弹簧在垂直方向上产生负刚度的同时，还会产生非线性刚度，并且推导出的负刚度与非线性刚度表达式都是经过泰勒展开得到的，展开后的公式会有无数的阶数，从而引入复杂的非线性动力学行为，甚至可能会有混沌响应，而工程上大多数情况下，并不希望有非线性，这样梁的稳定性会大大降低；

4、2、准零刚度弹簧所产生的负刚度在结构安装好时基本已经确定，如需改变负刚度值的大小，只有更换弹簧或者更改本体结构调整弹簧压缩量才能改变负刚度值的大小，而弹簧本身的刚度值受自身属性的影响，使用前都需要测量弹簧的准确刚度值，找到理想刚度的弹簧就会有所困难。

技术实现思路

1、为了解决上述技术问题，本发明提供一种弹簧和惯容器支撑的隔振器及隔振器固有频率调整方法。

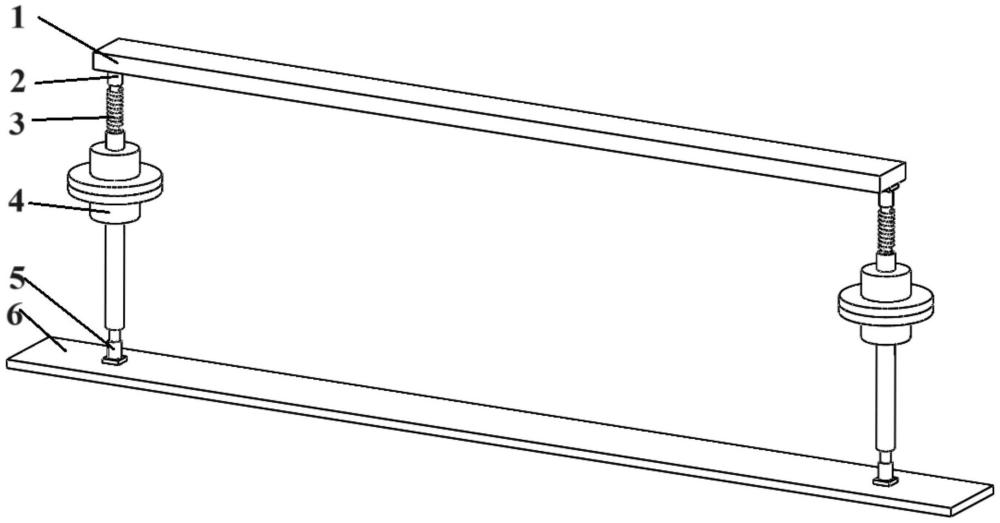
2、本发明是这样实现的，提供一种弹簧和惯容器支撑的隔振器，包括弹性梁、上轴支座、弹簧、惯容器、下轴支座和基板，弹性梁平行设置在基板上方，在弹性梁下表面两侧，分别设置一个上轴支座，在基板上表面两侧，分别设置一个下轴支座，在两侧的上轴支座与下轴支座之间，均设有一个惯容器，惯容器上端穿过弹簧与上轴支座固定连接，弹簧上端与上轴支座连接，下端与惯容器的外壳连接，惯容器下端与下轴支座固定连接。

3、优选的，所述惯容器包括上壳体、下壳体、丝杠、飞轮和定位轴套，上壳体扣接在下壳体上形成安装腔体，且在上壳体和下壳体扣接的位置形成水平方向的环形凸起内腔，上壳体上端设有供丝杠通过的上通孔，下壳体下端设有供丝杠活动的柱形腔，在上通孔上、柱形腔的上端均设有一个线性轴承，位于安装腔体内的丝杠外壁设有两个定位轴套，在两个定位轴套之间的丝杠上螺纹连接飞轮，飞轮位于环形凸起内腔内，丝杠上端穿过上通孔上设置的线性轴承后穿过所述弹簧，与所述上轴支座固定连接，丝杠下端穿过柱形腔上端的线性轴承后置于柱形腔内。

4、进一步优选，在所述丝杠外壁螺纹连接丝杠螺母，丝杠螺母外壁固定连接所述飞轮。

5、进一步优选，在所述下壳体的柱形腔外壁下端，设有与所述下轴支座连接的支撑轴。

6、本发明还提供一种隔振器固有频率调整方法，所述隔振器为上所述的弹簧和惯容器支撑的隔振器，所述调整方法包括如下步骤：

7、步骤1：得到所述弹性梁的边界条件：

8、ψ′(0)＝0，ψ′(l)＝0，

9、eiψ″′(0)+(kl-blω2)ψ(0)＝0，

10、eiψ″′(l)-(kr-brω2)ψ(l)＝0

11、其中，e、l、ρ、a、i分别为弹性梁的杨氏模量、长度、密度、横截面积以及惯性矩；kl与kr分别为左右两个所述弹簧的刚度系数；bl与br分别为左右两个所述惯容器的惯容系数；

12、步骤2：将chβx,shβx,cosβx,sinβx作为基础解系，通解为：

13、ψ(x)＝c1cosβx+c2sinβx+c3chβx+c4shβx

14、其中，cj(j＝1，2，3，4)为积分常数；

15、步骤3：将通解带入边界条件，进行求解得出β，将β带入求得固有频率ω；

16、步骤4：惯容器的惯容系数b的表达式为：

17、

18、其中，j为所述飞轮的转动惯量；p为所述丝杠的螺距；可知，惯容器只需更改转动惯量j即可改变惯容系数，从而改变负刚度值的大小，而转动惯量j仅与飞轮有关，故仅需更换不同飞轮的规格即可改变惯容系数；

19、步骤5：从步骤1中弹性梁的边界条件公式中的k-bω2可以看出，弹簧提供的正刚度与惯容器提供的负刚度构成隔振器的总刚度，通过更换飞轮，从而改变惯容系数，即可改变惯容器的负刚度，从而改变隔振器的总刚度，最终实现调整隔振器的固有频率。

20、优选的，步骤1中，所述弹性梁的边界条件是通过下述方法推导得到的：

21、步骤101：应用广义哈密尔顿原理，通过变分和分布积分导出弹性梁的动力学方程为：

22、

23、边界条件为：

24、

25、其中，t为时间坐标，x为弹性梁的轴向坐标，w(x，t)为弹性梁的横向振动位移；f0(x，t)为作用在弹性梁上的均布载荷激励，cl与cr分别为弹性梁左右两端阻尼的阻尼系数，λ为弹性梁的黏性阻尼；

26、步骤102：忽略方程中的阻尼项和非线性项，线性派生系统动力学方程及其边界条件如下：

27、

28、步骤103：假设解为：

29、w(x,t)＝ψ(x)q(t)；

30、其中，ψ(x)为弹性梁的模态函数，q(t)为相应的广义坐标；

31、将假设解带入到线性派生系统动力学方程及其边界条件中得：

32、

33、ψ′(0)＝0，ψ′(l)＝0，

34、eiψ″′(0)q(t)+klψ(0)q(t)+blψ(0)q″(t)＝0，

35、eiψ″′(l)q(t)-krψ(l)q(t)-brψ(l)q″(t)＝0

36、步骤104：系统动力学方程继续整理得：

37、

38、因为方程两边为不同自变量的函数，所以方程只可能等于常数，记作-ω2，导出方程1与方程2：

39、方程1：q″(t)+ω2q(t)＝0

40、方程2：eiψ(4)(x)-ω2ρaψ(x)＝0

41、步骤105：导出方程1为单自由度线性振动方程，其通解为：

42、q(t)＝αsin(ωt+θ)；

43、其中，α为振动的振幅，θ为振动的初相角，由初始条件确定；

44、将方程2简化为常系数微分方程：

45、ψ(4)(x)-β4ψ(x)＝0

46、其中，特征值β与固有频率ω的关系如下：

47、

48、步骤106：方程2的解确定弹性梁弯曲振动的振型函数，将chβx,shβx,cosβx,sinβx作为基础解系，将方程2的通解写作：

49、ψ(x)＝c1cosβx+c2sinβx+c3chβx+c4shβx；

50、积分常数cj(j＝1，2，3，4)及参数ω应满足的频率方程由梁的边界条件确定，可解出无穷多个固有频率ωi(i＝1,2,…)及对应的振型函数ψi(x)(i＝1,2,…)，构成系统的第i个主振动：

51、w(i)(x,t)＝αiψi(x)q(t)sin(ωit+θi)

52、其中，积分常数αi和θi(i＝1,2,…)由系统的初始条件确定；

53、步骤107：由方程1可得：

54、q″(t)＝-ω2q(t)；

55、将上述方程代入边界条件中，整理后的边界条件得：

56、ψ′(0)＝0，ψ′(l)＝0，

57、eiψ″′(0)+(kl-blω2)ψ(0)＝0。

58、eiψ″′(l)-(kr-brω2)ψ(l)＝0

59、与现有技术相比，本发明的优点在于：

60、本发明提供一种弹簧和惯容器支撑的隔振器及隔振器固有频率调整方法，主要针对隔振器中弹性梁结构自身受迫振动时，易产生机械共振，共振时，结构的振动非常剧烈，会导致不可预料的行为。本发明使用将惯容器加载于弹性梁结构的边界上的方法，为弹性梁结构边界提供负刚度，进而调整隔振器的固有频率，从而实现隔振效果，可以有效的避免机械共振的问题。