具有输入饱和的半潜式平台自适应预设时间动力定位控制方法

本发明涉及半潜式平台运动控制研究，尤其涉及一种具有输入饱和的半潜式平台自适应预设时间动力定位控制方法。

背景技术：

1、半潜式平台的运动主要依靠分布在其四周的数个侧推器提供的前进推力和转艏力矩来调整平台姿态以达到期望姿态。在ssp的动力定位控制过程中，首先建立ssps的运动学模型和动力学模型，其次构造平台期望位置与当前位置的误差，同时考虑模型不确定、海洋环境扰动、执行器幅值约束等问题，设计ssps的动力定位非线性反馈控制律，最后依据控制信号驱动执行器使得ssp达到期望控制状态。

2、在现有的算法中，已经提出一种基于鲁棒神经阻尼技术的控制器。将该算法记作算法a，其基于神经网络逼近技术设计船舶的动力定位控制律，并通过压缩神经网络权重构建自适应律。然而鲁棒神经阻尼技术虽然解决了系统的不确定性问题，但是当船舶的数学模型中的附体质量，惯性力矩及水动力导数变大时或者初始误差变大时，更新鲁棒神经阻尼项和自适应参数就需要更大的计算负载，同时也会加剧控制输入的超调。然而现实中船舶的侧推的动力是有限的，同时受机械结构和材料可靠性的影响，使得控制输入的幅值是客观受限，当控制输入超调到一定的界限会发生输入饱和现象。进而造成控制系统的不稳定，需要更多的时间和更大的输入使得系统稳定。

3、基于以上的分析，现有的鲁棒神经阻尼技术存在如下缺陷：

4、(1)当船舶模型参数变化时，不能保证含有鲁棒神经阻尼技术的控制器及自适应参数会不产生更大的计算负载和更多的稳定时间。

5、(2)当动力定位船舶的控制输入超调到一定界限达到饱和时，鲁棒神经阻尼技术不能处理系统输入饱和问题。

技术实现思路

1、本发明提供一种具有输入饱和的半潜式平台自适应预设时间动力定位控制方法，以克服上述技术问题。

2、为了实现上述目的，本发明的技术方案是：

3、一种具有输入饱和的半潜式平台自适应预设时间动力定位控制方法，具体包括以下步骤：

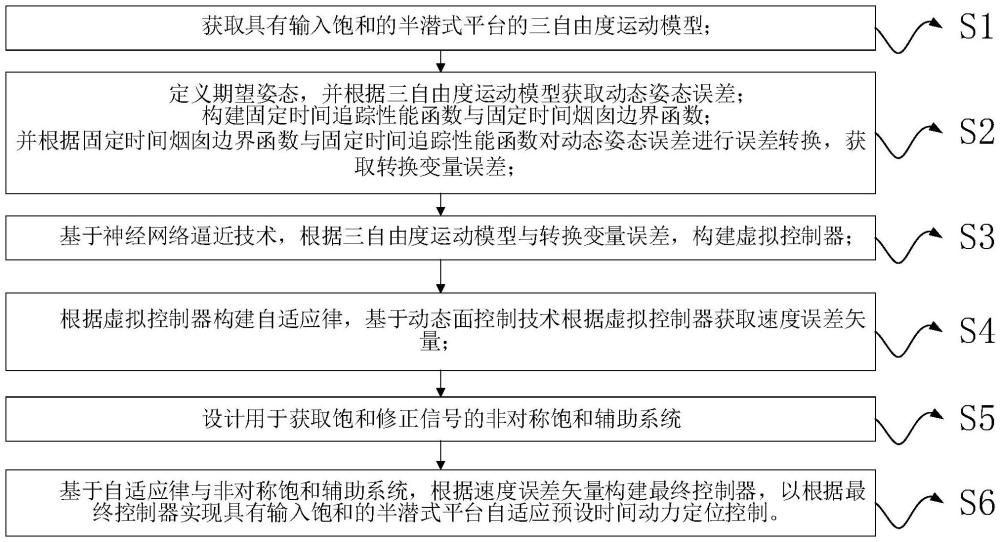
4、s1：获取具有输入饱和的半潜式平台的三自由度运动模型；

5、s2：定义期望姿态，并根据三自由度运动模型获取动态姿态误差；

6、构建固定时间追踪性能函数与固定时间烟囱边界函数；

7、并根据固定时间烟囱边界函数与固定时间追踪性能函数对动态姿态误差进行误差转换，获取转换变量误差；

8、s3：基于神经网络逼近技术，根据三自由度运动模型与转换变量误差，构建虚拟控制器；

9、s4：根据虚拟控制器构建自适应律，基于动态面控制技术根据虚拟控制器获取速度误差矢量；

10、s5：根据三自由度运动模型和分段输入饱和限制构建非对称饱和辅助系统；

11、s6：基于自适应律与非对称饱和辅助系统，根据速度误差矢量构建最终控制器，以根据最终控制器实现具有输入饱和的半潜式平台自适应预设时间动力定位控制。

12、进一步的，s1中所述具有输入饱和的半潜式平台的三自由度运动模型，如公式(1)所示

13、

14、式中：η＝[x,y,ψ]t表示半潜式平台ssp在惯性坐标系内的姿态矢量，(x,y)表示ssp的位置；ψ表示艏向角；r(ψ)表示速度旋转矩阵；ν＝[u,v,r]t表示ssp在附体坐标系内的速度矢量；u表示ssp的前进速度；v表示横漂速度；r表示艏摇角速度；m为惯性矩阵；n(ν)ν为包括附加质量、附加惯性力矩以及水动力的非线性导数项；τw＝[τwu,τwv,τwr]t表示海洋环境扰动向量，包含在ssp前进、横漂和艏摇自由度上的干扰力和力矩；τ表示在无饱和限制情况下的理想控制输入；τre表示真实控制输入；且三自由度控制输入力和力矩应满足公式(2)中的分段输入饱和限制条件，τmax,τmin分别表示半潜式平台ssp侧推力的上界限与下界限。

15、进一步的，所述s2具体包括以下步骤：

16、s21：定义期望姿态ηd＝[xd,yd,ψd]t，并根据三自由度运动模型获取动态姿态误差为ηe＝[x-xd,y-yd,ψ-ψd]t；

17、s22：构建固定时间追踪性能函数与固定时间烟囱边界函数；

18、所述固定时间烟囱边界函数μjν的表达式为

19、

20、式中：ηjν0,ηjνt,mj均表示正的可调节参数，且j＝1,2,ν＝u,v,r；tjν表示预先设定时间；μ1ν＝[μ1u,μ1v,μ1r]t与μ2ν＝[μ2u,μ2v,μ2r]t分别表示误差收敛过程中的上边界与下边界；

21、所述固定时间追踪性能函数的表达式为

22、

23、式中：kν,t0ν表示正的可调节参数；t0ν被表示为指定的预设时间；

24、s23：根据固定时间追踪性能函数对动态姿态误差进行误差转换，获取新误差变量υ(t)为

25、

26、式中：ηe表示ηe(t)的简写形式；ηe(0)表示动态姿态误差ηe(t)的初始值；

27、s24：根据固定时间烟囱边界函数μjν获取新误差变量υ(t)的非对称性能约束为

28、-μ1ν(t)＜υ(t)＜μ2ν(t)                       (6)

29、s25：引入中间变量转换公式，并根据新误差变量υ(t)与非对称性能约束获取转换变量误差；

30、所述中间变量转换公式为

31、

32、ρ(t)＝(μ1ν-μ2ν)/2，γ(t)＝(μ1ν+μ2ν)/2                 (9)

33、式中：表示中间变量转换公式的输出；ρ(t),γ(t)表示中间参数变量；

34、所述转换变量误差z1为

35、

36、进一步的，所述s3具体包括以下步骤：

37、s31：根据三自由度运动模型与转换变量误差，获取转换变量误差导数z1的动态方程，其表达式为

38、

39、式中：φ(t)表示中间参数量，且

40、s32：定义为转换变量误差导数的动态方程的不确定项，基于rbf-nns逼近技术中的非线性连续函数f1(η,a1)在线逼近此不确定项，其表达式为

41、

42、式中：a1表示权重矩阵；s1(η)表示拥有高斯函数形式的rbf基函数矢量；s1表示s1(η)的简写形式；η表示姿态矢量且作为非线性连续函数f1(η,a1)的输入矢量；εη表示逼近误差项；

43、s33：根据转换变量误差z1结合步骤s32构建虚拟控制器，且所述虚拟控制器的表达式为

44、

45、式中：kη＝diag{kη1，kη2，kη3}分别表示在x,y,ψ三个自由度上的虚拟控制器参数；a1表示正的设计参数；θ1表示自适应参数且θ1＝||a1η||2；表示对θ1的估计值。

46、进一步的，所述s4具体包括以下步骤：

47、s41：根据虚拟控制器构建自适应律，且所述自适应律为

48、

49、式中：γ1,γ2,均表示正的自适应设计参数；νe表示待求解速度误差矢量；

50、其中自适应参数θ2＝||a2ν||2，具体为基于rbf-nns逼近技术中的非线性连续函数f2(ν,a2)，在线逼近三自由度运动模型中的非线性导数项n(ν)ν获得，其表达式为

51、n(ν)ν＝f2(ν,a2)＝s2(ν)a2ν+εν (15)

52、式中：f2(ν,a2)表示非线性连续函数；a2表示权重矩阵；s2(ν)表示拥有高斯函数形式的rbf基函数矢量；εν表示非线性导数项的逼近误差项；

53、s42：基于动态面控制技术根据虚拟控制器获取待求解速度误差矢量νe；

54、s421：通过动态面控制技术的滤波器，消除虚拟控制器连续求导而造成控制律的复杂度爆炸问题，所述滤波器的表达式为

55、

56、式中：tν＝diag{tu,tv,tr}为时间常数矩阵；βν表示输出矢量为速度矢量ν的参考信号；βν(0),αν(0)分别表示βν与αν的初始值；

57、s422：根据输出矢量βν与饱和修正信号获取待求解速度误差矢量νe，其表达式为

58、

59、式中：θ12,θ22表示饱和修正信号，且θ12＝[λu12,λv12,λr12]t,θ22＝[λu22,λv22,λr22]t；λu12,λv12和λr12分别代表在三个自由度上的一阶修正信号；λu22,λv22和λr22分别代表在三个自由度上的二阶修正信号；i表示单位向量；p1,p2表示正的饱和辅助参数，且p1＞0,p2＞0。

60、进一步的，s5中用于获取饱和修正信号的非对称饱和辅助系统，其表达式为

61、

62、式中：g-(τ,τmin),g+(τ,τmax)表示中间参数量。

63、进一步的，s6中基于自适应律与非对称饱和辅助系统，根据速度误差矢量构建最终控制器，其表达式为

64、

65、式中：k2＝diag{k21,k22,k23}分别表示在u,v,r三个自由度上的控制器参数；σ2与a2表示正的设计参数。

66、与现有技术相比，本发明的有益效果：

67、(1)结合所构建的固定时间追踪性能函数(fttpf,fixed-time trackingperformance function)使得最初的动态姿态误差转换为不受初始条件影响的误差形式，再结合误差转换函数构造出系统的转换变量误差，从而使得动态误差更大程度地被限制在边界内。同时当系统达到设定的预设时间时，使得转换变量误差信号成功稳定收敛。

68、(2)所设计的非对称饱和辅助系统成功解决了船舶驱动器的物理限制导致的输入饱和问题。除此之外，尽管船舶模型参数，水动力导数变化，非对称饱和辅助系统依旧能够解决因驱动器的输入限制对控制系统造成的奇异性问题。

69、(3)通过神经网络逼近技术对ssp动力定位系统中的非线性项进行在线逼近，并且通过自适应技术设计了执行器增益自适应律。