一种四旋翼无人机的姿态控制方法与流程

本发明属于四旋翼无人机，具体涉及一种四旋翼无人机的姿态控制方法。

背景技术：

1、四旋翼飞行器具有飞行稳定、机动性强、垂直起降、自由悬停、狭窄空间飞行和便于携带等优点，成为近年来的研究热点之一。由于四旋翼飞行器是一种典型的非线性、强耦合、多变量的欠驱动系统，为保证其良好的控制效果和飞行效果，对飞行控制算法进行研究，提高飞行器的控制性能和鲁棒性具有重要意义。

2、目前，针对四旋翼飞行器飞行控制算法的研究，大部分是关于姿态稳定控制的方法，包括线性控制算法如pid控制算法、线性二次型调节器(linear quadratic regulator,lqr)控制算法等，非线性控制算法如反馈线性化控制算法、反步法、滑模变结构控制算法、h∞控制算法、模糊控制算法等。

3、现有控制算法都具备一定的鲁棒性，但是抗干扰能力较弱，如较为经典和常用的pid控制算法，在较强的干扰下的控制效果并不理想。而四旋翼飞行器在外界真实环境下进行轨迹跟踪飞行时，会同时受到多种外界干扰，以及自身参数的不确定性和内部噪声干扰，要求飞行控制系统具有很强的自适应性和抗干扰能力。但大部分情况下，四旋翼飞行器受到的干扰并不能直接测量，或者测量成本太高，使得干扰抑制较难实现。除此之外，在实际操作中，对于传统ladrc存在难以获得比例微分增益值的缺陷，这会导致控制器无法提供足够的干扰补偿。

4、综上，四旋翼无人机姿态控制方法的抗干扰能力和鲁棒性已经无法很好的满足四旋翼飞行器的需求，为此，针对四旋翼飞行器的干扰抑制问题，本发明提出了一种四旋翼无人机的姿态控制方法。

技术实现思路

1、本发明的目的是提供一种四旋翼无人机的姿态控制方法，针对无人机系统有着动态性能好，抗干扰能力强和鲁棒性好的优点，满足四旋翼飞行器的需求。

2、本发明采取的技术方案具体如下：

3、一种四旋翼无人机的姿态控制方法，包括以下步骤：

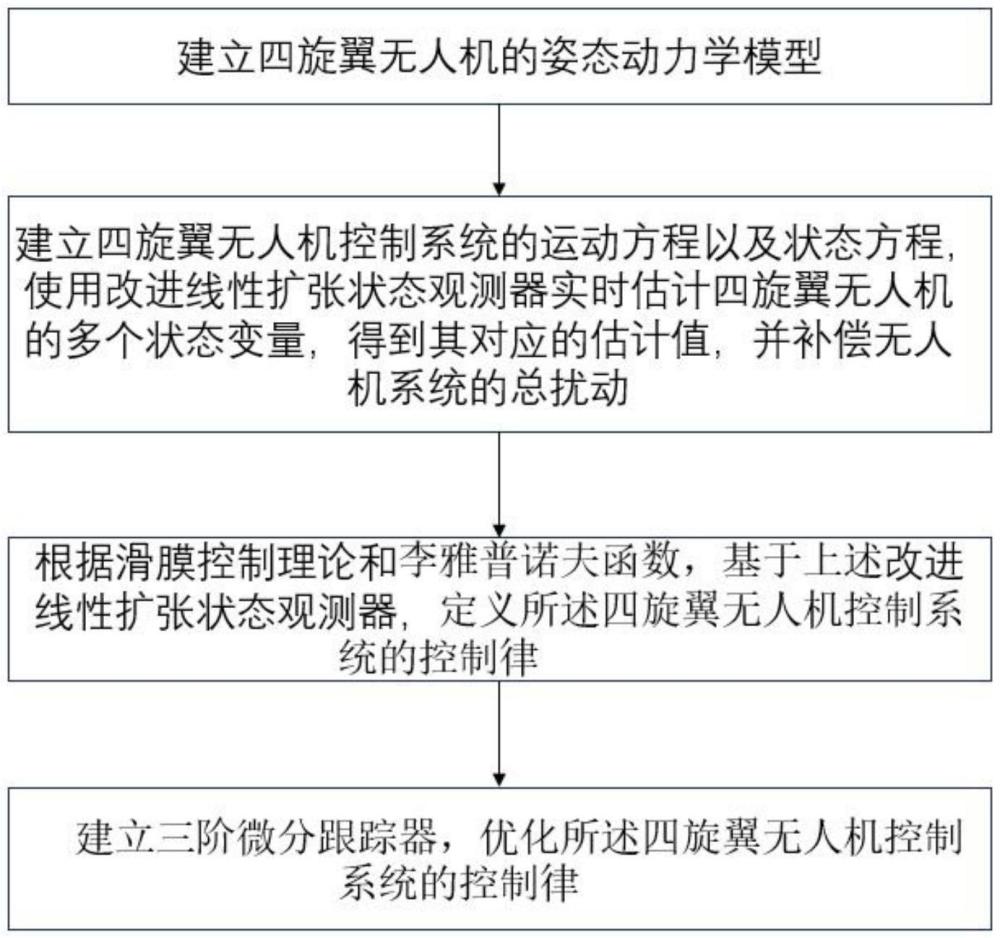
4、步骤一：建立四旋翼无人机的姿态动力学模型；

5、步骤二：建立四旋翼无人机控制系统的运动方程以及状态方程，使用改进线性扩张状态观测器实时估计四旋翼无人机的多个状态变量，得到其对应的估计值，并补偿无人机系统的总扰动；

6、步骤三：根据滑膜控制理论和李雅普诺夫函数，基于上述改进线性扩张状态观测器，定义四旋翼无人机控制系统的控制律；

7、步骤四：建立三阶微分跟踪器，优化四旋翼无人机控制系统的控制律。

8、2.根据权利要求1所述的一种四旋翼无人机的姿态控制方法，其特征在于：所述步骤一包括以下步骤：

9、首先，根据四旋翼无人机的动力学特性及牛顿欧拉方程建立动力学模型：

10、

11、其中，(x,y,z)为四旋翼无人机的空间坐标，为x对时间的二阶导数，即为x方向的加速度，同理，为y方向的加速度，为z方向的加速度；m为四旋翼无人机的质量，b为升力系数，g为重力加速度，ω为旋翼转速，φ、θ、ψ分别为横滚角、俯仰角、航向角，分别为机体绕x轴，y轴，z轴的角速度，分别为机体绕x轴，y轴，z轴的角加速度，(ix，iy，iz)分别为机体xx、yy、zz方向转动惯量，l代表机体中心到电机转子的距离，d代表反扭距系数；空间三轴x、y、z通道和横滚角φ、俯仰角θ、航向角ψ通道的未建模部分以及模型不确定等信息分别用δx、δy、δz、δφ、δθ、δψ表示；

12、然后搭建无人机的动力模型：

13、

14、其中，为对应电机的转速，b为升力系数，l代表机体中心到电机转子的距离，u1为四个电机驱动螺旋桨带来的总升力t，u2、u3和u4为x、y、z三轴力矩，d代表反扭距系数。

15、进一步地，所述步骤二包括以下步骤：

16、首先，设计改进线性状态观测器，结合步骤一中式子(1)和式子(2)，整理可得：

17、

18、其中，为内环各个通道的总干扰，(δφ、δθ、δψ)分别代表系统内部得不确定扰动项；

19、由式子(3)，可将四旋翼无人机的二阶控制系统的运动方程表示为：

20、

21、其中，y为输出，u为输入，f为系统扰动量，b0为系统控制增益；

22、定义x1＝y,x3＝f,x3为二阶控制系统的扩张状态变量，可得：

23、

24、其中，x1，x2，x3为状态变量，由式子(5)可得状态空间方程为：

25、

26、其中，c＝[1,0,0]；

27、则对应的状态观测器为：

28、

29、其中，l＝[β1 β2 β3]t是线性扩张状态观测器(leso)的误差反馈增益矩阵；而线性扩张状态观测器的增益的特征方程如式(8)所示：

30、λ＝s3+β1s2+β2s+β3＝(s+ω0)3   (8)

31、则增益矩阵为：

32、

33、则可得leso公式为：

34、

35、其中，z1,z2,z3为x1，x2，x3的估计值，β1β2β3为观测器增益；

36、而为了使控制系统更稳定，可对上述线性扩张状态观测器(leso)进行改进，由式子(8)可得传递函数为：

37、g(s)＝β3/(s3+β1s2+β2s+β3) (11)

38、将这个三阶系统近似为中频带的二阶系统进行分析：

39、

40、由式子(12)可知，与β1、β2相比，β3的设计对系统性能的影响更大；因此，对β3的改进如下：

41、β3＝β4(1+β5s) (13)

42、其中，β4，β5是常规参数，是将β3改进设计的比例导数项，β4，β5的值需要通过调参得到合适值；

43、由上式可得新的传递函数为：

44、

45、进一步地，所述步骤三包括以下步骤：

46、首先，根据得到的改进扩张状态观测器，设计基于状态观测器的滑模姿态控制器，结合上述式子，定义观测误差为：e1＝z1-y，则ileso为：

47、

48、令y的期望值为yd，设计滑模面为：

49、

50、其中，e表示系统输出y和期望输出的差值；

51、设系统的李雅普诺夫函数为：

52、

53、结合式子(3)、式子(15)和式子(16)，可得

54、

55、其中，对于φ和θ通道：i＝ix；对于ψ通道：i＝iz；

56、为了满足滑模存在和逼近条件，选择以下切换控制律：

57、

58、根据滑模控制理论，减小η和增大k可以加速收敛过程；

59、其中，η、k是常数参数；

60、然后，由式子(18)和(19)，可推导出基于辅助系统的滑膜控制律为：

61、

62、则式子(18)可化为：

63、

64、其中，

65、进一步地，所述步骤四包括以下步骤：

66、在存在噪声和干扰的情况下，对于式子(20)所示的控制律，根据上述控制律设计三阶td来实现其输入信号的导数计算；

67、所述步骤四中的三阶td表示为：

68、

69、其中，r和δ是要调节的参数；ud是跟踪的输入信号；分别是输入指令的跟踪值、输入指令的导数和输入指令的二阶导数；

70、因此，姿态环的控制律变为：

71、

72、其中，u9t)是smc控制器的输出值，也是姿态环的控制律，是s的观测值。

73、本发明取得的技术效果为：

74、本发明的一种四旋翼无人机的姿态控制方法设计了鲁棒性较强的滑模姿态控制器(smc)，并在smc的基础上引入了加入了比例微分增益的改进线性状态观测器(ileso)，既对干扰进行外部观测和补偿，又减少峰值时间，提高系统的响应速度，使得系统响应速度更快，通过设计三阶微分跟踪器，辅助滑模控制和ileso，不仅提高了无人机姿态控制系统的精度和响应速度，还增强了系统对噪声和干扰的抵抗能力，从而使得无人机能够在各种飞行条件下保持稳定和精确的姿态控制，针对无人机系统有着动态性能好，抗干扰能力强和鲁棒性好的优点，满足四旋翼飞行器的需求。