一种机器人的惯性定位方法及系统

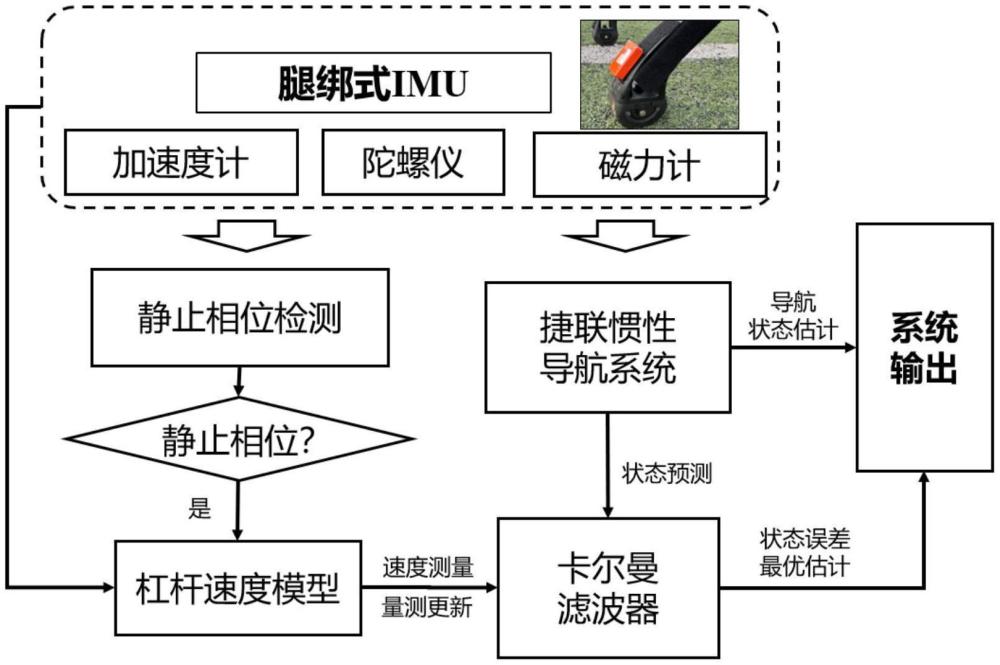
本发明涉及机器人定位领域，具体涉及一种机器人的惯性定位方法及系统。

背景技术：

1、随着机器人技术的发展，可以行走的机器人由于其优越的地形适应能力和灵活性，越来越受到关注和应用，而其中，腿式机器人对定位精度的要求更高，然而，腿式机器人的精准定位问题一直是一个技术难题。传统的定位方法主要依赖于外部传感器，如gps、uwb超宽带等，但这些方法在室内或信号受阻环境中往往会失效。惯性测量单元由于其独立性和不受外界环境影响的特点，成为腿式机器人定位系统中的重要传感器。

2、现有技术中，利用imu进行腿式机器人定位的方法通常需要将imu放置于机体内，通过复杂的运动学约束，并融合传感器数据以提高定位精度。这种方法不仅增加了系统的复杂性和成本，还增加了数据处理的难度和机器人建模负担。安装在机体内的imu传感器容易受到零偏、噪声，没有固定状态观测，容易产生积累误。此外，机器人运动学模型容易受到地形影响，使得在机器人的步态周期中，脚部产生打滑，因此传统依赖运动学模型的腿部里程计往往受到关节编码器噪声和误差积累的影响，存在定位精度低、实用性不强的问题。

技术实现思路

1、发明目的：本发明目的是提供一种精度更高、实用性强、过程简单的机器人的惯性定位方法及系统。

2、技术方案：本发明所述的机器人的惯性定位方法，包括如下步骤：将imu固定于机器人足部，初始化所述imu后进行数据采集；导航系统基于捷联惯性导航原理处理所述imu采集的数据，实时解算所述机器人足部的速度、姿态、位置；建立足部相位检测模型处理所述imu采集的数据，当检测到机器人足部处于静止相位时，利用杠杆速度模型计算机器人足部的估计速度；根据所述速度和所述估计速度估计导航误差状态，并由所述导航误差状态修正所述机器人足部的速度、姿态、位置。

3、进一步的，初始化所述imu包括如下过程：

4、建立imu的机体系；

5、对所述机体系进行零偏校正；

6、在校正后的所述机体系中求解初始姿态。

7、进一步的，通过如下公式计算所述零偏：

8、

9、式中，t1表示静态区间开始时刻，t2表示静态区间结束时刻，w表示陀螺仪三轴输出；表示零偏；

10、通过如下公式求解初始姿态，包括俯仰角和滚转角：

11、

12、式中，ax、ay、az组成imu的机体系三轴的比力输出{ax,ay,az}；γ表示滚转角；θ表示俯仰角。

13、进一步的，所述导航系统基于捷联惯性导航原理将imu的机体系转换为导航系统的导航坐标系，并对姿态、速度、位置进行导航坐标系下的实时解算；对姿态的解算过程如下：

14、

15、式中，q表示四元数；表示imu机体系到导航坐标系的坐标转换矩阵；ψ表示航向角；γ表示俯仰角；θ表示滚转角；

16、对速度实时解算的公式如下：

17、

18、式中，vn,k是imu在导航坐标系下的速度，下标n表示导航坐标系，k+1和k分别表示解算前后时刻；fb表示加速度计输出的比力；是地球自转角速度在导航坐标系下的投影；是导航坐标系相对于地球坐标系的地球自转角速度投影；δt是更新时间间隔；

19、对位置实时解算的公式如下：

20、pn,k+1＝pn,k+vn,kδt

21、式中，δt是更新时间间隔；vn,k是imu在导航坐标系下的速度；pn,k表示当前时刻导航坐标系下位置估计；pn,k+1表示下一时刻导航坐标系下位置估计。

22、进一步的，建立所述足部相位检测模型包括如下过程：

23、利用广义似然比检验模型处理imu采集的数据，得到多个时刻的检测统计量，并计算检测统计量的自适应阈值；由所述检测统计量、自适应阈值建立如下足部相位检测模型：

24、

25、式中，t(n)表示n时刻的检测统计量；γn表示自适应阈值；g＝1时，为静止相位，g＝0时，为摆动相位。

26、进一步的，所述杠杆速度模型如下：

27、

28、式中，为由杠杆速度模型产生的imu的速度估计值；为imu在机体系下的三轴角速度输出；是机体系下的旋转半径向量。

29、进一步的，基于卡尔曼滤波方法估计导航误差状态，具体包括如下过程：

30、建立导航系统的导航误差状态方程；

31、根据所述速度和所述估计速度建立速度误差观测方程；

32、由所述导航误差状态方程与速度误差观测方程建立卡尔曼滤波框架，并通过离散化求解导航误差状态。

33、进一步的，所述状态方程为：

34、x＝ax+gw

35、式中，x表示十八维导航误差状态，且其中，表示平台误差角，δv表示速度误差，δp表示位置误差；εw表示陀螺的零偏误差，εa表示加速度计的一阶马尔可夫漂移误差，hos表示旋转半径误差；a表示状态转移矩阵；g表示导航系统噪声转移矩阵；w表示导航系统噪声；

36、所述速度误差观测方程为：

37、

38、式中，z表示观测向量；表示由惯性导航系统解算得到的机器人足部速度；vlvm表示由杠杆模型得到的机器人足部估计速度；h为观测矩阵；x为导航系统误差状态；nv为测量噪声；

39、经过离散化卡尔曼滤波得到导航状态误差后验估计：

40、

41、式中，h表示观测矩阵；z表示观测向量；表示由导航误差状态方程得到k时刻的状态先验估计；xk为由卡尔曼滤波器求解得到导航误差状态的后验估计。

42、进一步的，求解出的所述导航误差状态包括加速度计偏差、陀螺仪偏差、姿态偏差、速度偏差、位置偏差；

43、通过姿态偏差、速度偏差、位置偏差修正所述机器人足部的速度、姿态、位置；通过加速度计偏差、陀螺仪偏差修正所述imu中加速度计、陀螺仪的输出。

44、本发明所述的机器人的惯性定位系统，包括：

45、部署模块，用以将imu固定于机器人足部，初始化所述imu后进行数据采集；

46、状态解算模块，用以使导航系统基于捷联惯性导航原理处理所述imu采集的数据，实时解算所述机器人足部的速度、姿态、位置；

47、速度估计模块，用以建立足部相位检测模型处理所述imu采集的数据，当检测到机器人足部处于静止相位时，利用杠杆速度模型计算机器人足部的估计速度；

48、状态修正模块，用以根据所述速度和所述估计速度估计导航误差状态，并由所述导航误差状态修正所述机器人足部的速度、姿态、位置。

49、有益效果：本发明具有如下显著效果：1、精度更高：本发明结合imu进行数据获取的基础上，建立了足部相位检测模型、杠杆速度模型对数据进一步优化，通过惯性导航原理解算imu数据实现机器人可靠导航与定位；具体的，实时处理imu数据进行捷联惯导状态解算，并通过静止相位检测方法判断足式机器人的足部静止相位，在静止相位内应用杠杠速度模型得到实时速度观测向量，最终在卡尔曼滤波器中进行数据融合，得到后验估计的导航误差状态，然后反馈修正导航定位误差，能够有效提取足部的静止和摆动相位，并结合滤波的方法对imu的速度进行有效观测，弥补了腿式机器人惯性可靠导航问题，有效抑制了惯性导航系统的误差发散，解决了仅使用惯性测量单元导致腿式机器人导航定位误差累积严重的问题，提升腿式机器人导航定位精度，具有实时性好、可靠性强的优势，适合于工程应用；2、实用性强：本发明提出的方法适用于多种路面，包括但不限于草地类的柔软地面、水泥类的坚硬地面，应用的范围更大，场景更复杂，实用性强；3、过程简单：本发明将imu设置于机器人外部，减少了安装在机器人内部容易出现的零偏、噪声，没有固定状态观测，容易产生积累误等情况，并且不需要复杂的运动学约束而处理imu采集的数据，过程更为简单，减少了数据处理的难度和建模的过程，成本更低更高效。