基于混合元启发式算法的在线多机器人避障路径规划方法

本发明涉及机器人导航，尤其涉及一种基于混合元启发式算法的在线多机器人避障路径规划方法。

背景技术：

1、多机器人系统在当下的日益复杂精密的生产生活中占据了越来越重要的角色。原因是，多机器人系统具备更高的任务执行效率，更高的鲁棒性以及对复杂任务的更高实用性。故被广泛地应用于野外搜救与侦察、物流配送、自动化生产、水域和空域环境监测等。尽管该系统所涉及的控制程序和智能化程度已经发展了较长时间，但关于提高多机器人系统的工作效率的研究仍有待加强。这是由该系统对于无人化程度的要求决定的，所以该类系统中的机器人又被称为无人驾驶车辆。无人驾驶车辆包括无人驾驶地面车辆（ugv）和无人驾驶航空器（uav）。在多机器人系统的自治性和无人化协作性的要求下，该系统对参与智能决策的算法要求较高。而在其多数应用领域中，自主导航的能力强弱决定了该类机器人执行任务的成败和执行任务的效率。其中路径规划则是机器人自主导航技术的需要关注的重点问题之一，也是自主导航的技术突破口。

2、在线路径规划问题涉及机器人或自动驾驶车辆在动态环境中实时计算和更新位置，找到最优或者可行路径。与离线路径规划不同的是，在线规划需要对突然出现的障碍物，以及多变的交通状况做出实时反应。在线路径规划的主要挑战在于环境感知的准确性，决策的高效性，以及路径的安全性。所以，在线路径规划要求算法具备较高的求解速度、求解准确性以及鲁棒性。

3、经典的路径规划算法有基于图搜索的算法如dijkstra和a算法等；基于采样的算法如，快速探索随机树（rrt）、概率路线图（prm）等；基于启发式的算法，如人工势场法等；基于学习的算法，如强化学习；基于元启发式的通用算法，如粒子群优化（pso），蚁群优化（aco）,遗传算法（ga）等。而由于在线多机器人路径规划问题的特性，传统的dijkstra和a算法不适用于复杂和动态环境。而rrt和prm尽管适合处理复杂问题和复杂环境，但是路径质量不佳。人工势场法则问题依赖性较强，且容易陷入局部最优。基于学习的算法在复杂问题上的计算代价较大。故而，基于元启发式的通用算法以其问题独立性和及时动态响应性渐渐被用于求解不同类型和不同场景下的机器人路径规划问题，并获得了广泛关注。而coa的局限在于容易陷入局部最优和探索行为不足等。此外，对于在线多机器人路径规划而言，coa在复杂环境下的搜索到最优路径的概率完备性不高。

技术实现思路

1、本发明的目的是提供一种基于混合元启发式算法的在线多机器人避障路径规划方法，以解决上述现有技术中存在的问题。

2、为了解决上述问题，根据本发明的一个方面，提供了一种基于混合元启发式算法的在线多机器人避障路径规划方法，包括以下步骤：

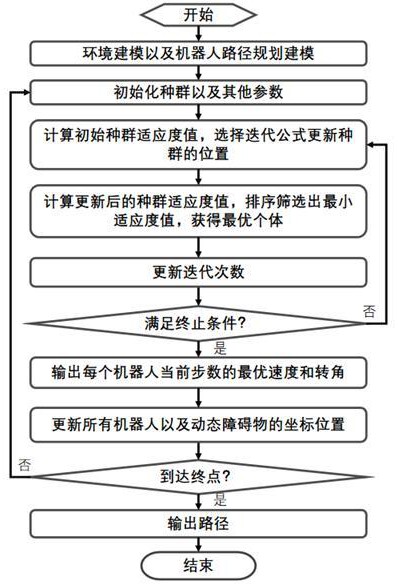
3、s1、环境建模以及机器人路径规划建模，包括设定机器人的起点和终点，即设定机器人的初始路径；

4、s2、根据机器人的数量和对应的速度和转角；设定输入的参数矩阵的维度，即初始化种群中的每个个体位置及参数，对s1中机器人的初始路径进行优化；

5、其中，随机的初始解矩阵x的计算公式：

6、；

7、其中，n代表种群大小，d代表设计变量的维度，即机器人的速度和转角的总维度，ub和lb分别代表搜索空间的上界和下界，即机器人速度的上下界，rand是一个n×d的随机矩阵，所有值均在0-1之间；

8、s3、计算初始种群适应度函数值及平衡参数temp的值，选择相应迭代公式更新代理位置； 如果用表示第i个个体在当前迭代次数的位置，是第i个个体更新后的位置；

9、其中，适应度函数值计算公式：

10、；

11、其中，表示所有机器人在当前步数内累计行驶距离，表示所有动态障碍物与所有机器人在当前步数的累计距离，表示所有静态障碍物与所有机器人在当前步数的累计距离，表示当前步数内累计的惩罚值，表示括号内所有项对于总步数的累计值，

12、平衡参数temp值的计算公式：

13、；

14、rd为 [0，1) 之间的随机数；t为当前迭代次数；t为最大迭代次数；tsca-ub和tsca-lb分别是温度缩放因子的上，下界，均为常数，值分别为1.3和0.5；

15、若temp的值大于或等于30，则采用避暑或竞争行为，若temp的值小于30，则采用觅食行为，通过选择避暑、竞争行为或觅食行为中的迭代公式来更新代理位置；

16、s4、计算更新后的种群的适应度函数值获得当前最优个体的适应度函数值，即对更新后的种群中的所有个体计算适应度函数值，通过排序可以得到最小的适应度函数值；

17、s5、更新迭代次数，判断是否满足迭代终止条件；

18、s6、若不满足迭代终止条件，则返回至s3；若满足迭代终止条件，则执行下一步；

19、 s7、输出迭代后的最小适应度函数值以及每个机器人当前步数的最优速度和转角；

20、 s8、更新所有机器人的位置坐标以及动态障碍物的位置坐标；

21、 s9、判断所有机器人是否到达终点；

22、 s10、若所有机器人没有到达终点，返回至s2；若所有机器人到达终点，则执行结束，输出所有机器人的路径。

23、在一个实施例中，其中，s1中，环境建模包括设定机器人的起点和终点，静态障碍物的位置，以及动态障碍物的起点和终点；机器人路径规划建模包括机器人动力学模型的建立以及机器人的避障行为模型建立。

24、在一个实施例中，其中，在s1机器人的避障行为模型中，假设机器人的数量是nr，静态障碍物的数量为ns，故第i个机器人与静态障碍物之间的欧式距离可以表述为：

25、；

26、其中，和表示第k个静态障碍物的横坐标和纵坐标，和是第i个机器人可选的下一个坐标位置，

27、其运动方程可表述为：

28、；

29、和分别为当前位置的横坐标和纵坐标，和分别为当前这一步的速度和转角，和分别为动态障碍物下一个位置的横坐标和纵坐标。

30、在一个实施例中，其中，当某个机器人已选的下一个位置的坐标与障碍物的坐标之间的欧式距离在危险距离范围内时，执行惩罚机制，过程可以描述为：

31、；

32、其中，表示惩罚系数，是一个常数；danger-1、danger-2、danger-3分别表示第i个机器人与静态障碍物，动态障碍物和其他机器人的危险距离。

33、在一个实施例中，其中，避暑行为包括第一种避暑行为和第二种避暑行为，

34、第一种避暑行为使用公式：

35、；

36、其中， 表示第i个个体在当前迭代次数的位置，是第i个个体更新后的位置，lf是由莱维飞行所决定的随机数所组成的矩阵；c1是改进的缩放因子，rd1和rd2表示种群中随机的两个个体的索引，h为常数，值为8；t表示当前迭代次数；r1和r2分别为 [0，1) 之间的随机数，表示索引值为rd1的个体在第j维的位置，表示索引值为rd2的个体在第j维的位置，表示当前迭代次数内的最优个体，

37、第二种避暑行为使用公式：

38、；

39、其中，表示第i个个体在第j维的当前位置；表示第i个个体在第j维的更新后的位置；r3表示 [0，1) 之间的随机数；c1是改进的缩放因子；rd3和rd4表示种群中随机的两个个体的索引，cov表示指数收敛因子，表示索引值为的rd3个体在第j维的位置，表示索引值为rd4的个体在第j维的位置；cov的表达式为：

40、；

41、其中w为常数，其值为4；

42、在一个实施例中，其中，竞争行为包括第一种竞争行为和第二种竞争行为，

43、第一种竞争行为使用公式：

44、；

45、其中，其中r4，r5表示 [0，1) 之间的随机数，rd5和rd6表示种群中随机的两个个体的索引，表示索引值为rd5的个体在第j维的位置，表示索引值为rd6的个体在第j维的位置，

46、第二种竞争行为使用公式：

47、；

48、其中，表示第i个个体在第j维的位置；表示某个随机个体在第j维的位置；表示当前种群中的最优个体；表示第i个个体在第j维的更新后的位置；。

49、在一个实施例中，其中，进食行为包括第一种进食行为和第二种进食行为，

50、第一种进食行为使用公式：

51、；

52、其中r8，r9表示 [0，1) 之间的随机数；p为鳌虾的进食率，

53、；

54、其中，代表了最适宜鳌虾觅食的温度，值为常数25，和c3用于控制不同温度下鳌虾的进食率，值分别3和0.2，

55、第二种进食行为使用公式：

56、；

57、；

58、其中r10表示 [0，1) 之间的随机数。

59、本发明的有益效果在于，针对coa的局限性，提出了改进的coa。具体改进体现：

60、1）在coa的基础上引入bwo的开发策略，设计了新的并行式组合开发行为，即第一种避暑行为和第一种竞争行为。旨在增强算法的灵活性，解的精确度，以及最优解的搜索概率完备性。

61、 2）设计了新奇的探索策略即第二种避暑行为，旨在扩大算法的搜索范围，增加种群多样性和潜在最优解被发现的概率。

62、3）设计了凸型收敛因子，用于平衡算法的搜索和收敛速度，有利于提高算法对不同问题的适应性收敛变化的能力。

63、4）改进了算法中控制探索与开发平衡的参数，使其具备了一定弹性变化，有利于提高算法对于动态复杂问题的适应性。