一种基于运动学模型的双机器人协同误差的标定方法
- 国知局
- 2024-09-14 14:40:30
本发明属于工业机器人标定,具体涉及一种基于运动学模型的双机器人协同误差的标定方法。
背景技术:
1、工业机器人广泛应用于搬运、焊接、装配等领域,但目前大多数场景都是基于单机器人的应用,即使一条生产线上有很多机器人,各个机器人也大都在各自的工位上各司其职,相互之间没有太多的配合和联系,对双机器人或多机器人协调技术的应用较少。为了适应任务的复杂性、操作的便捷性和系统的柔性,需要将传统单机器人模式扩展为双机器人协调作业,即两台机器人通过一定的协调策略相互配合完成预期任务。
2、以大型机翼部件的机器人自动化搬运和装配为例,通常的做法是在机器人末端安装多对吸盘来进行吸附,但是难以克服部件尺寸过大带来的抖颤问题,这对飞机装配来说是必须解决的。又比如航空作业中双向电磁铆接,需要精确保证双机器人末端的运动配合紧密。以上例子涉及到多机器人协同作业的典型场合概括起来有:大尺寸、弱刚性或超过单机器人负载物体的搬运和精密装配,以及必须通过机器人协作才能完成的工作,如电磁铆接、冷作成型和超声检测等。此外为提高效率而进行的协作,比如同时进行焊接等也是常见的应用场景。而要在多个机器人末端上进行位姿的协同,其协同精度是我们关注的重点:协同精度差会导致任务失败、工件或机器人受损等后果。因此,双机器人乃至多机器人系统的协同定位精度是机器人推广应用亟需解决的关键技术之一。
3、机器人精度标定相关的研究已较为成熟,按照是否实时补偿误差分为在线和离线标定两种,后者又可分为基于运动学模型标定和非运动学模型标定。基于运动学模型的标定方法一般会对运动学参数和基坐标系参数进行标定;非运动学模型标定一般指的是运用神经网络模型技术等进行标定。
4、现有技术有采用离线标定方法中的非运动模型标定,通过测量双机器人的位姿,并以关节角度为训练数据,训练两个ann模型来对绝对精度和相对精度分别进行补偿,使得主从机器人的精度有较为明显的提高。该方法将双机器人系统视为“黑盒”,一定程度上忽略了各种误差来源的区别,可是ann模型的参数物理意义并不清晰,对揭示机器人精度补偿的内在机理并无帮助。同时该方法训练数据量需求较大,时间成本较高,文中测量了800对位姿数据。
5、基于运动模型的标定中,目前主要侧重于基坐标系标定策略的研究。有研究人员在双机器人末端安装反射纸,采用双目视觉系统测量了机器人末端不在同一平面的四个点,建立并求解了其齐次方程得到双机器人基坐标系的相对位姿关系。一般来说,依靠定制工具的方法在标定过程中需要依赖人工操作和判断,这制约了标定的效率和精度。
技术实现思路
1、本发明所要解决的技术问题是针对上述现有技术的不足,提供一种基于运动学模型的双机器人协同误差的标定方法,考虑影响多机器人协同精度耦合运动学参数误差、机器人基坐标系误差、工具坐标系误差,将d-h模型运动学参数误差、基坐标系建立误差、工具坐标系建立误差统一建模,成功应用于双机器人的标定,显著提升双机器人的协同精度,降低了协同误差的波动。
2、为实现上述技术目的,本发明采取的技术方案为:
3、一种基于运动学模型的双机器人协同误差的标定方法,包括:
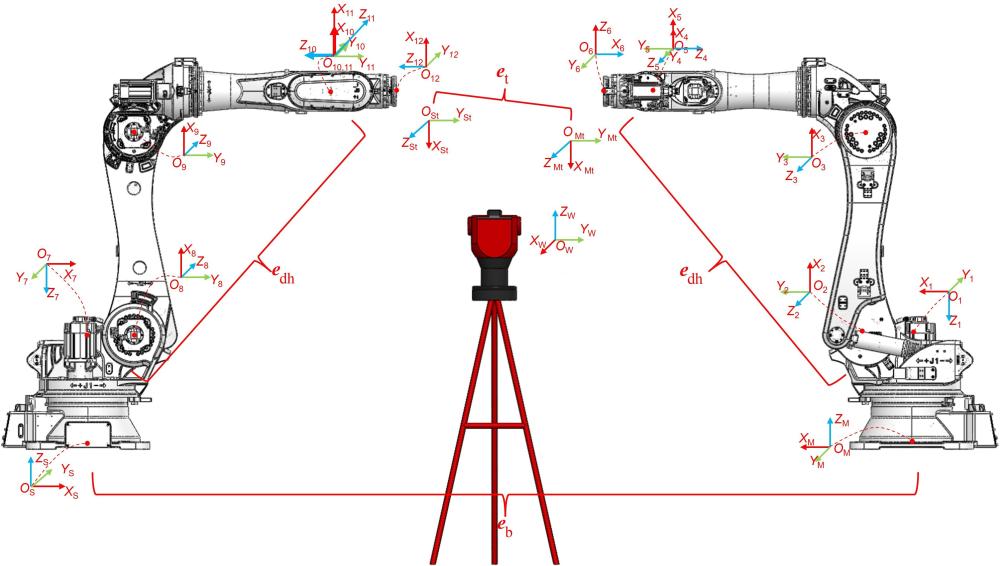
4、步骤s1:根据主机器人相对于基坐标系的变换矩阵、从机器人相对于基坐标系的变换矩阵、基坐标系相对于世界坐标系的变换矩阵以及双机器人相对于世界坐标系实际关系,给出双机器人协同误差的定义;
5、步骤s2:基于主机器人连杆坐标系与其工具坐标系之间的转换关系,构建双机器人工具坐标系拟合误差模型;
6、步骤s3:基于基坐标系建模误差,构建双机器人基坐标系拟合误差模型;
7、步骤s4:基于将d-h模型运动学参数误差,构建双机器人连杆参数误差模型;
8、步骤s5:基于步骤s1的定义以及步骤s2-步骤s4构建的模型,以协同误差最小化为目标,利用l-m算法对双机器人的参数误差进行辨识和标定。
9、为优化上述技术方案,采取的具体措施还包括:
10、上述的步骤s1构建的双机器人的协同误差根据下式表达:
11、;(7)
12、其中,和分别代表主机器人工具坐标系相对于主机器人基坐标系、从机器人工具坐标系相对于从机器人基坐标系的变换矩阵;
13、和分别表示主机器人基坐标系和从机器人基坐标系相对于世界坐标系的变换矩阵;
14、和分别表示主机器人工具坐标系和从机器人工具坐标系相对于世界坐标系实际关系;
15、通过分析双机器人的几何关系,将上式的协同误差表示为:
16、;
17、其中、、分别为机器人工具坐标系拟合误差引起的误差、基坐标系拟合误差引起的误差和双机器人连杆参数误差引起的误差。
18、上述的步骤s2基于下式构建双机器人工具坐标系拟合误差模型:
19、;
20、;
21、式中,为主机器人第6号连杆坐标系与主机器人工具坐标系之间的转换关系,分别为主机器人第6号连杆坐标系绕主机器人工具坐标系按 z-y- x欧拉角方式旋转的角度,分别为主机器人第6号连杆坐标系相对于主机器人工具坐标系沿 x, y, z轴的平移距离,,其他以此类推,表示行列的0向量,和分别是主机器人第6号连杆坐标系相对于主机器人工具坐标系的位置误差向量和姿态误差向量,和分别是从机器人工具坐标系相对于从机器人第12号连杆坐标系的位置误差向量和姿态误差向量,代表相应参数的误差,分别为从机器人工具坐标系绕从机器人第12号连杆坐标系按 z-y-x欧拉角方式旋转的角度,分别为从机器人工具坐标系相对从机器人第12号连杆坐标系沿 x, y, z轴的平移距离;
22、构建的双机器人工具坐标系拟合误差模型为:;(9)
23、式中,
24、;
25、中的前三个表示从机器人工具坐标系相对主机器人第6号连杆坐标系齐次变换矩阵的旋转向量,最后一个为平移向量,其他以此类推。
26、上述的步骤s3根据下式构建双机器人基坐标系拟合误差模型:
27、;
28、;
29、;
30、;
31、;
32、构建的双机器人基坐标系拟合误差模型为:;(13)
33、式中,
34、;
35、;
36、;
37、;
38、;
39、分别为从机器人基坐标系绕主机器人基坐标系按 z-y-x欧拉角方式旋转的角度值,为从机器人基坐标系原点相对主机器人基坐标系分别沿 x, y, z轴的距离,中的前三个表示从机器人工具坐标系相对从机器人基坐标系齐次变换矩阵的旋转向量,最后一个为平移向量。
40、上述的步骤s4构建的双机器人连杆参数误差模型为:
41、;(27)
42、式中,
43、;(28)
44、为3×6矩阵,各矩阵第列向量的表达式为:
45、;
46、;
47、;
48、为3×6矩阵,各矩阵第列向量的表达式为:
49、;
50、。
51、上述的步骤s5中,基于步骤s2-步骤s4建立双机器人协同误差与各种参数误差之间的数学矩阵模型,以辨识出参数误差,进而补偿协同误差,对机器人进行标定,双机器人的协同误差矩阵为:
52、;(29)
53、式中,为考虑多源误差的机器人雅克比矩阵,为所有误差组成的列向量;
54、以公式(29)所示的误差矩阵最小为目标,利用l-m算法辨识出相应的,具体计算公式为:
55、;(30)
56、式中,表示阻尼因子,为单位矩阵。
57、上述的辨识的过程为:
58、(1)计算第 k次迭代时的考虑多源误差的机器人雅克比矩阵;
59、(2)基于机器人雅克比矩阵和优化因子计算第 k次迭代所对应的参数误差;
60、(3)基于第 k次迭代所对应的参数误差计算第 k次迭代时实际下降量与预估下降量的比值;
61、(4)基于比值更新第次迭代时的机器人参数误差和优化因子;
62、(5)当满足设定条件时,结束循环,此时的得到的参数误差为最优参数误差,完成机器人的标定。
63、本发明具有以下有益效果:
64、本发明为了提高双机器人协同工作的协同精度,提出了双机器人的协同误差的定义和表示方法,建立了耦合运动学参数误差、机器人基坐标系误差、工具坐标系误差的扩展运动学误差模型,提出了一种考虑这三种误差源的双机器人协作系统运动学标定方法,将d-h模型运动学参数误差、基坐标系建立误差、工具坐标系建立误差统一建模,且成功应用于双机器人的标定,本发明可显著提升双机器人的协同精度,降低协同误差的波动,可以使得在较小的随机采样规模下,辨识参数误差,补偿后机器人协同误差提升明显且效果稳定。
本文地址:https://www.jishuxx.com/zhuanli/20240914/295452.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 YYfuon@163.com 举报,一经查实,本站将立刻删除。
下一篇
返回列表