一种基于激波耦合场降维导控的工作面制造方法及装置与流程

本发明涉及一种基于激波耦合场降维导控的工作面制造方法及装置，属于激波耦合。

背景技术：

1、人类的工业生产技术发展至今，已经形成39个工业大类、190多个中类和500多个小类，而中国是目前全世界唯一拥有全部工业门类和唯一的全产业链国家，能够生产从日用消费品到航空航天、从原料矿产到工业母机的一切工业产品。

2、与大规模全产业链不相称的，是整体工艺技术的集约化水平和程度仍相对较低，导致效能低等问题。比如作为日常消费品的一次性打火机，其生产工艺其实相当复杂：需要abs注塑成的外壳，冲压形成的防风罩，引火簧、面阀、按手、滤芯、海绵垫、调火环、翘板、打火石等几十个元器件，涉及到十几个不同的工艺和几十种不同加工设备。又如汽车制造，拥有最长的产业链条，从零部件、元器件制造到各系统总成、再到整车组装，涉及80多个领域，其动力总成、电控系统、底盘架构、转向机构、制动系统等，每一个功能系统都需要十几到几十上百个工序工艺环节的组合，仅仅一个铝轮毂的制造，就需要合金配料、熔炼、净化、转注、铸造成型、粗加工、无损探伤检测、热处理、精加工、热喷涂等10多道工序才能完成，过程复杂，作业线长。

3、产业链长、作业线长的一个整体缺陷是能耗高、效率低。管理上尽可以通过增加劳动力岗位、分工协作来提高效率，通过制定和执行严格的工艺技术和质量标准来降低能耗，但这些都是被动的做法：对于一个定型的生产线和产业链，其能耗有理论下限，生产效率有理论上限，作业人员只能无限接近临界点而无法突破。如此一旦工艺技术发生根本性变革，新的能耗理论下限和产率上限出现，将淘汰大批的落后产能，放在国际竞争大视野中，产业革命造成的损伤和损害也是巨大的，甚至不可弥补。

技术实现思路

1、本发明要解决的技术问题是：提供基于激波耦合场降维导控的工作面制造方法及装置，用“创造和应用高能态冲击波”来解决前述关于现有工业制造技术中存在的产业链长、作业线长的整体缺陷和能耗高、效率低等技术问题。

2、本发明采取的技术方案为：一种基于激波耦合场降维导控的工作面制造方法，利用冲击波与工作介质在耦合场中发生先耦合、后解耦的混沌效应，再利用场控降维手段，对解耦工作介质进行从准四维耦合场向准二维耦合场的降维映射导控，对接不同的工作界面，实现工业制造或加工。

3、所述耦合及解耦，是指冲击波能量与介质相互作用时产生的急剧升压到极点后随即自然降压的物理效应。其中，压力p随时间t变化关系(p-t曲线)反映在脉冲图像中的升压段，存在时间约为纳秒尺度(1ns＝10-9s)，称为耦合；在正高压极点之后自然降压的现象和过程称为解耦。

4、所述混沌效应，是指冲击波在工作介质中的初始传播和散发(内外质点群“耦合－解耦”依次递延传播的态传递)，因符合“自组织临界性”，而导致参与质点数量增大和脉冲能级递降的迭代性状符合近似幂律，进而在系列的“耦合－解耦”过程发生的难以精确描述的能级衰减、速度衰减同时带动质点群直到整个工作介质体系都发生运动的趋势。

5、所述准四维耦合场，是指冲击波能量与介质的耦合态，由于是一个产生和存在时间极短(纳秒尺度)的高能物态质团，具有自发“衰变”即解耦的特性，解耦时间和解耦体积都达到耦合态的数百倍至近千倍；耦合态包含了3d体积加上“准一维的折叠能量(时变能)”，故称耦合态为准四维耦合场。

6、所述准二维耦合场，是指冲击波与介质的混沌效应之后经“狭缝宽面”的扁平型出口约束而形成的高压涡旋射流态。该准二维耦合场的形成机制在于，被冲击波扰动的大量质点处于具有一定的动能但运动方向沿波阵面发散的状态，为将这些动能集中起来加以利用，而以“射流空间→出口场导流”的场控降维和映射手段，把三维流动的质点群用“狭缝宽面”的扁平型出口场(称为准二维场)进行的压缩性约束和导流；由于是由四维耦合场的“点状体积”经过混沌传播、延时映射而形成的流场质点群，其表面积较初始态表面积具有千万倍率以上的增量，准四维耦合场的能量维度已经与准二维场形成充分的融合分布，即形成了质点群的高压流动张量场(势能张量与动能张量之和)，等效于二维膜的热涨落加剧，故称此流动态为准二维耦合场。

7、所述工作界面，是指利用冲击波生成的高能涡旋流体(态)进行工业制造或加工的实际界面，其物理意义是界面层的质点群及其代表的本征结构，特别是，质点群及其本征结构在冲击波场中是宏观动态变化的，在冲击波消解后，可以是宏观静态或者凝固态。

8、优选的，所述场控降维手段，是指运用压力场或电磁场中的至少一种配合冲击波能量的维度降解，使流态化质点群实现靶向流动的方法，包括：利用出口为扁平型“狭缝宽面”内腔的、设有流体介质进出口的椭圆半球+倒喇叭状复合型腔结构的压力容器，实现高压流体介质涡旋射流态的降维映射；或者利用熔丝与工件之间的电磁场、电脉冲和电弧热达到瞬时熔化和敷铺，实现质点连续地从丝材向工件表面和缝隙的降维映射；或者利用高速机械工具对工件上质点群实施持续有序的高速碰撞，实现质点群的定向剥落或定向重构的降维映射；或者利用激光从凝聚态材料上剥落原子或原子团簇或准分子质点，实现向靶标定向输送原子或原子团簇态质点的降维映射；或者利用超强磁约束场，对可聚变等离子体产生极高压涡旋态，并使之在约束环形场中悬浮绕流，实现向靶标定向输送核聚变等离子体的降维映射。

9、优选的，对于流态化工作介质，一次冲击波脉冲完成一个当量数的物质合成或者分解，并通过耦合场的出口以扁平形的涡旋射流态喷出，与之后的工作界面对接；所述冲击波的单个脉冲的能级当量，按照混沌态控制模型结合能量参数进行计量和调控，具体如下：把冲击波在流体中的作用场，即冲击曲面s，分割成无穷多份，并将每一份的面积记为ds，那么冲击能量通过每一小份的流量dφ作为φ的散度量，可以由能流密度ed与其对应的面积元ds的乘积表示，即dφ＝edds，对散度积分可得所需冲击波的能级强度，在这一模型框架下，流(熔)体中冲击波的能量标度，或者冲击波脉冲的能级当量需满足以下条件之一：

10、

11、①当以波在流体中一个等效截面上的能流密度ed表示时，须满足不等式ed＞σaf，式中σaf代表流体中任一位置的面积元内的表面或界面的张力或界面能；

12、②当以波的传播相速度cp表示时，须满足不等式cp＞σif/ηm，式中σif代表流体的界面张力或界面能，ηm代表流体的动力黏度；

13、③当以波在流体中引起的质点拟动速度cn表示时，须满足不等式cn＞(retηm)/(dρm)，式中ret代表流体处于紊流或湍流状态的雷诺数，ηm代表流体的动力黏度，d代表聚焦冲击波形成的焦斑直径；前述质点拟动速度cn，是指把流体看成牛顿流体，把冲击波压力看成流体驱动力的情景下，以微分视角观察流体体积元质点可以获得的初始瞬时速度，不代表宏观尺度上流体介质的速度；

14、④当以冲击波场在流体中的作用半径r及该场界面的压力pf表示时，须满足不等式rpf＞σif，式中作用半径r代表冲击波源点或焦点到流体冲击波场界面的距离，σif代表流体的界面张力或界面能；

15、⑤当需要冲击波执行对凝固界面进行重新熔化、使结晶质点重新具备流态化特征，或者使熔体表现为近超流态时，引入的冲击波能级标度选择，应首先考虑熔体合金的热容热e＝3nkbt和熔化潜热lm这两项之和，而后再考虑按上述ed＞σaf、cp＞σif/ηm、cn＞(retηm)/(dρm)、rpf＞σif的一种或几种，进行引入到流体中的冲击波能量φ值的设计，比如φ＞3nkbt+lm+σaf；

16、⑥保障冲击波-介质发生强烈耦合的能量是泰勒经验公式e＝ρcr5/t2，可设φ＞ρd/t2，这里的c是耦合介质的热容比，可通过实验比较获得；r可以根据需要进行调整，比如需要喷射涡旋流打到多远的距离d，按d＝cr5/n进行折算(n取正整数，如1，2，3，…)，通过实验得到不同r值，再通过变分法求取对应的d值。

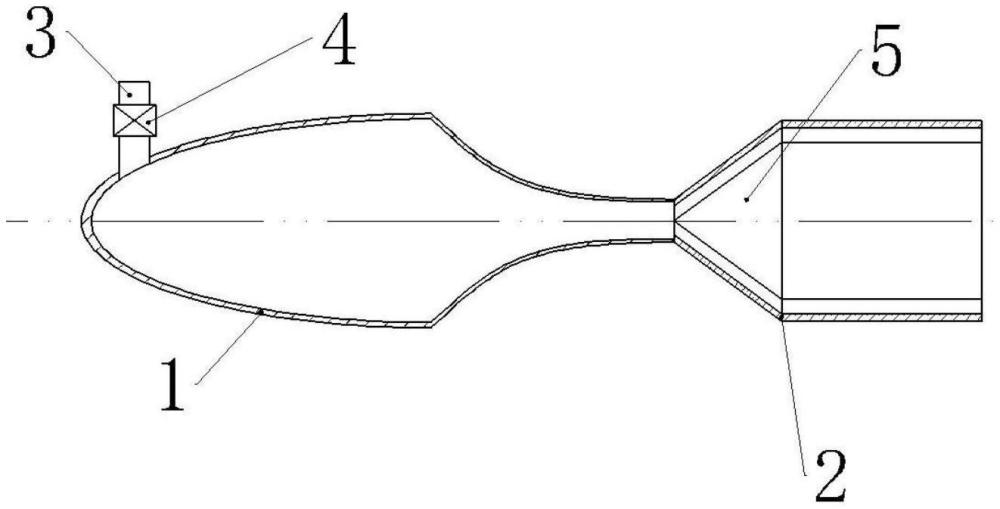
17、本发明还公开了一种激波耦合场降维导控的工作面制造装置，对于液态工作介质，包括椭圆半球+倒喇叭状复合壳形型腔的压力容器，所述容器上的椭圆半球部分设有液态的工作介质进口，所述容器上的倒喇叭状部分设有液态的工作介质出口，所述容器的出口端连接有喷嘴，所述容器中充满液态的工作介质。

18、优选的，所述喷嘴的流道型腔截面是扁椭圆形，扁椭圆半短轴为1～10mm，半长轴为半短轴的10～100倍。

19、优选的，所述喷嘴的流道型腔包括喇叭口段和直管段，所述喷嘴流道型腔的喇叭口段用于对接容器，所述喷嘴流道型腔的喇叭口内部设置有圆锥面导流体，所述直管段用于对接模具型腔。

20、优选的，所述容器内部盛满液态金属熔体介质，腔体上设有液态金属输入口和所需合金元素的输入口，能调节输入量与每次冲击波脉冲导致的喷嘴喷出物质当量相适应。

21、优选的，所述容器由合金熔体在一定压力和温度条件下经液相合成得到，所述温度≤1000℃。

22、优选的，所述合金熔体包括铝合金熔体、镁合金熔体以及因为溶质溶解度小、溶剂与溶质密度差异大而通常需要强烈机械搅拌的合金熔体中的一种，合金熔体的搅拌由自身的涡流涡旋实现。

23、本发明的研究思路如下：

24、在凝聚态物理领域，一百多年来研究的热点此起彼伏并不断发展。从20世纪初人类进入到电气化时代，调控电荷和晶体结构成为研究材料、器件的热点，20世纪中后期集成电路、芯片的出现使人类进入信息化时代，电子电荷及调控的应用达到顶峰，成为生物、医学、物理、化学以及天文等学科关注的核心之一，随着宇宙演化理论、黑洞、暗物质的深入探索，人类已经来到“二次量子革命”的前夜。

25、将材料研究和制造技术置于“扰动法调控材料微结构”的基础之上，把晶体及非晶态物质的宏观性能研究引入到微结构层次研究，并通过微结构调控，研制新颖的高功能基材、组件与元器件，积极推动在微结构层次上凝聚态物理、材料及器件的发展，是国际先进材料发展的主导方向。该方向自1960年代以来在推动激光材料、半导体材料、纳米材料、压电陶瓷、电磁材料、石墨烯、高温超导材料等的发展上取得了巨大成功，理论积淀和检测手段也取得了长足进展，奠定了量子物理理论及工程技术应用于工业生产、科学实验和日常生活许多物质基础，如原子力显微镜、激光致冷、原子组装、互联网、手机、自动化终端等。

26、以人工智能ai、高速大容量数字信息化技术(新一代基础芯片及算法、空天网络及其终端设备)、受控核聚变技术、室温超导技术、高能电磁和激光技术、超冷技术、高效能交通物流网络等为代表的人类第四次工业革命，目前正在加速进程中，其本质，实际上仍是致力于制造能力和水平的极大提高，即实现更快、更强、更高效能。而要达到这样的目标，获取“高能态和高能态调控”是一个首要的核心问题，而“冲击波”(也叫激波，shock wave，sw)是高能态联系材料层次结构之宏观物态与微观结构的一个主要线索。

27、冲击波具有显著的宏观态变效果，其基础却在于对材料微结构的扰动形成了微质点群的集群式应激反应，类似于激光产生的机理，即从波动力学的观点来看，激光与激波都具有波的属性。从能量的发射、接受、态变和传递的角度看，机械加工或高速碰撞，与黑体辐射、热辐射、光电效应、x射线、牛顿摆、声传播、电磁效应、激光、太赫波、雷达信号、爆炸、超临界效应、超流超导效应等类似，虽然形式和形态千变万化，其基础其实都是一个：物质与能量的交互作用，或者更确切地说，是凝聚态(大多数情况是晶格网格结构)对于不同能级标度的能量流(气流、液流、电流、电磁波、声波、机械波、冲击波等)的接受、应激、传导和反馈。机械加工作用不过是这种物理过程的一个环节而已。随着测量技术的进步，人们发现微结构的变化可以对宏观加工效果造成巨大影响，新材料的研发本质上是建立在微结构调控的基础上的，于是，根据这种影响而设计建造了更先进的加工技术装备，推动了材料、元器件、零部件和集成技术的进步。

28、为了进一步提高效能，顺承“二次量子革命”和“四次产业革命”并助推这种趋势，有必要在分析冲击波的本质、作用和价值基础上，进行新型制造方式的设计或改进。

29、雷击破坏可能是人类感受的第一类冲击波事件，那时候面对这种突如其来的灾害没有科学的认知也无法躲避，只能归结为“天神发怒”之类的想像。人类运用冲击波最早是在军事上，以火药爆燃获取高能态的气流冲击波，赋予枪弹和炮弹以高强动能，比传统的弓弩箭矢具有更强大的毁伤能力。对空气动力学的研究则表明物体行进速度超过声速就会形成激波，由此而发明了超音速飞行器。对“弹丸—靶体”间高速碰撞的研究揭示了固体内冲击波发生和传播的一些特点。医学上可以用液电冲击波来做对人体无损伤的内脏结石破碎手术(体外冲击波治疗)。利用高压水枪、激光、等离子体、电火花等高能物态造成的冲击波可以进行金属材料的切割加工。而高能电脉冲－电弧热能够在瞬间完成对焊丝端头的熔化并利用剩余的能量把熔滴推射到工件表面或焊缝中，这个过程是电压－电流的功率冲击波能量大部分转化为对焊丝材料的加热升温(热容热)和熔化潜热，只有很小部分供给对熔滴的推送。

30、电火花和电弧都是电脉冲表现的能量释放形态之一，它们因电磁和高压电离击穿效应而致热，以极高的效能实现金属导体材料的瞬间高温熔化和“微区重构”，达到从固态到液态的相变，从而实现切割功能，而当熔融态因冷却而再度凝固时，又能把原来分离的固态材料连为一体。由此可见，高能的电脉冲冲击波通过“瞬态相变”，既能实施分割加工，又能执行连接组合。对于室温作业环境来说，只要能够实现对金属等晶体材料的“瞬态熔化”这一个相变，自然能够达成材料的“分离”和“连接”两种功能，因为高熔点液态材料的凝固是可以自然发生的。由此，电磁热工工艺可以实现离解和连接两种相反的制造方式的统一，具有高效制造的潜力。

31、瞬态熔化，在宏观尺度上不容易实现，在微观尺度上则可以利用电磁效应实现。量子物理研究指出，室温自然状态原子晶格的振荡频率为1012hz，即每秒达万亿次以上，通过电流脉冲的电磁效应叠加原子振荡(类似荡秋千的推送效应)，使之越过系统平衡态的势能壁垒，原子们挣脱其平均晶格势阱的限制，成为半自由的团簇组合态，在宏观上即可成为流体——在宏观上需要快速升温到上千摄氏度又须充分供给熔化潜热的分段式复杂物理过程，在微观结构调控机制下变得十分简单而短暂，因为具体有多少个原子、晶粒或质点参与了叠加振荡，以及各质点振荡的强度具体多大，是不需要关心的，我们只要控制电流强度(电压)和脉冲频率就可以，显然，这在宏观上须体现为一种冲击波效应，即能量集中于小区域质点集群(焊丝端头)以产生突变效应。

32、关于单次脉冲所能熔喷的质量有多大，理论上似乎可以计算，但在对冲击波深入研究之前主要依赖于试验和经验积累。比如，枪型、炮型、弹型和火炸药当量规定了每颗子弹或炮弹的装药量，是枪械和弹药长期运用、改进、研发等技术经验积累的结果，又如，焊机提供的电压电流、焊丝材质、端头与工件距离及其伸缩频率等决定了焊丝熔喷质量和消耗速度，也是焊接工艺长期运用、改进、技术经验积累的结果——质量参数看起来是可以根据目的和需要进行灵活调控的；从理论计算的角度看，具体的质量数首先看冲击波脉冲能量大小，然后看耦合材料本身的理化性能如导电导热性、密度、热容、熔化潜热、液态黏度等，以及是否经过“固→液相变”或者其它类型的相变，还有耦合体积、耦合温度、熔喷速度随时可变——这属于典型的“时间短暂、经历复杂”的过程，影响因素太多且多变，计算结果也不可能精准。由此可见，量子范域内的物质与能量问题，因遵从“不确定性原理”，要获得宏观状态精确定量的能量密度和对应质量，不能只依赖计算，首先是要通过不断地试验，实测，积累数据，细分用途，明确目标，然后再建模、优化、检验，循环往复，直到形成一个领域一种目标的工艺路线和技术标准，即建立“宏观确定性”，再开发相应的专用设备组合，以保证目标达成，然后降本增效，批量生产。

33、冲击波脉冲及其与工作介质的耦合，显然具有量子物理的特征，即具有不确定性，每个脉冲需要多少能量或者多大功率，无法、也没有必要精确计算，从宏观态考虑，关键是在于必须能够提供高于“能级下限”的能量需求，达到宏观显著性，以此作为“宏观确定性”的最低能级标度。从微观的不确定性到宏观态下的确定性，这中间有一个变化的尺度问题，自然状态下物质材料的微结构之间存在着永不停息的相互扰动，但并不能引起体系宏观的态变，体系保持着静态的平衡，这样的扰动只能视为微弱扰动。而强烈的扰动则能够打破体系的静态平衡，使体系发生确定的宏观态变，相应地，可将造成宏观形态变异的扰动称为“强扰动”。

34、“强扰动态”在材料学方面的另一描述，是“短历时过程的大变形、大变性”，比如高速碰撞、爆炸、高压击穿、系统突然崩塌或恒星坍缩等，这些现象的共同特征，是由于高强度扰动(一般是高能量脉冲冲击波涨落效应)超过了物质材料的抗力而导致的本构特征的突然性破坏。但是，对于开发新材料来说，利用高强度扰动探测材料的极限性能，或者达到常规手段无法实现的材料性能提升，是一个新的角度，值得深入研究。这需要把结构静力学与结构动力学、高速碰撞动力学领域的知识和技术联系起来，同时把经典力学与量子力学、牛顿运动方程与波动方程等学科领域的物理数学方法结合起来。

35、冲击波的微观不确定性和宏观确定性，必然涉及到具有“自组织临界性－近似幂律的长程关联”的现象及规律，即混沌态，在这个理论的框架下，冲击波的宏观效应，与物质相变、天气变化到出现降雨、森林出现火灾、雪崩、大脑活动等现象具有类似的动力学特征，即所谓爆发动力学，其典型特征，是“系统对初始条件的极端敏感性”。

36、冲击波和耦合效应。最具表征性的冲击波是核爆(nuclear explosion)。1945年7月16日人类试爆了第1颗原子弹，爆炸当量大约2万吨tnt(即8.4×1013j)，对此美军方只公布了一系列反映爆炸后火球随着时间扩展的照片(其中包括0.10ms到1.93ms等时间间隔的14帧火球照片)，比如冲击波球面半径在25ms内膨胀到130米(图1)；但1950年，英国力学家g.i.泰勒在原子弹各种数据信息仍处于绝密状态时，仅仅根据公布的照片序列，就将原子弹释放的能量e计算了出来，其估计值非常接近美国总统后来公布的值(差值约15％)。他创造的计算公式为e＝ρr5/t2，是按照“量纲齐次/凑单位”原则，假设核爆球形冲击波半径r，仅仅依赖于爆炸后的时间t、爆炸瞬间所释放的能量e、无量纲常数c以及空气密度ρ，从归一化原则得到r＝ctx eyρz，分别用长度、时间、能量、密度的国际单位进行代入衡量，即可求得x、y、z值。由此得到r＝c(et2/ρ)1/5,因c是比热比的低阶函数，无量纲，在任何条件下都近似为1。则可以推出爆炸所释放的能量为e＝ρr5/t2。这就是核爆冲击波能量的泰勒经验公式[1]。

37、注意到在该式中，e∝r5＝r3·r2，而4πr3/3是球的体积值v，4πr2是球的表面积值s，因此，原子弹或其冲击波能量，作为极短暂瞬间(从约10-15秒到约10-4秒)释放的点源超高功率能，在其有效作用时间和空间内，是突破了凝聚态物质以原子键合势能为根本组合架构的特征态，从而对其作用范域内的一切物质和物体，达成了架构解体(做高倍体积功)和表面质点离散(把表面能“清零”)的毁灭性效果，即超高温高压汽化直至等离子体化。这种瞬间的态变跨越了几个相变(固、液、气及各种中间相)，是高能态的“质-能耦合”，相当于遭遇数学或物理学意义上的“无穷大”，核爆点可称为“时空奇点(spacetime singularity)”。

38、如果把r5替换成冲击波火球体的体积v和表面积s的关系，则g.i.泰勒推导的核爆冲击波能量对有效作用时空的关系式可写成：e＝3ρvs/(4πt)2。这样就清晰地揭示出sw冲击波能量e与其有效作用范域球体(球谐函数)的体积v、表面积s和时间t的关系，即耦合态(coupling st ate)。耦合态中的时间t只能处于费秒(fs，10-15s)、皮秒(ps，10-12s)、纳秒(ns，10-9s)、微秒(μs，10-6s)、毫秒(ms，10-3s)的时限以内，分别对应着核裂变、原子响应、晶格响应(光电效应)、晶核团簇序破坏、晶界响应破坏的时间尺度。更大的时间尺度则触及到宏观的凝聚态特征，属于高能耦合态对称性破缺、质点粒子无序性和离散性增加、物质开始出现长程序序参量主导表观物性的经典物理学范畴，即“混沌态中的有序性”。反之则可认定，冲击波是量子物理学、或者量子物理向经典物理过渡的范畴，必须立足量子物理观念并结合、借鉴经典物理学的科学手段研究冲击波现象和事件。总之，冲击波产生的“瞬时性”通常只能在毫秒或微秒以下，除非核爆级当量，或者具有同步球面对称性的汇聚波，毫秒或更长的响应时间一般不足以导致冲击波事件。

39、时间尺度对应的空间尺度一般具有相同或相近的格或级，即费秒(fs)、皮秒(ps)、纳秒(ns)、微秒(μs)、毫秒(ms)分别对应着费米(fm，10-15m)、皮米(pm，10-12m)、纳米(nm，10-9m)、微米(μm，10-6m)、毫米(mm，10-3m)。但是，对于具有球面对称或圆弧面对称的汇聚波，由于具有“同步向心”的运动特征，即使起始于较大的尺度，仍然能够形成冲击波效应，比如钱塘江潮，从海面向喇叭口倒灌的水波同步汇聚到较窄江桥附近、遭遇堤坝阻遏时，就会突然激发数丈高的冲击波。这是大容量潮汐溯流能量串级(energy cascading,又称ec效应)达到尺寸同步，终于达到质能交互形成强大耦合场的结果。而同步特征，直接联系着物质时空分布和运动的对称性原理及其对称性破缺理论，是宇宙大爆炸、规范对称性及动量、能量、角动量守恒理论和法则的底层逻辑。

40、核爆冲击波巨大的破坏性，促使人们对其物理效应及其发生机理的深入研究，进而推动了科技的进步。其中，sw能量释放的瞬时性和强扰动性，产生了以“点爆小范围局域性事件”对作用介质的“大范围局域性结构变态”的效果，“核弹小范围”与“灾难大范围”形成极其强烈的对比，即点爆邻近介质(有效作用空间内)在瞬间发生跨越式相变，而当sw过后更大范围空间的介质又力图把破坏的状态回复至原始态——却又不能完全回复(因为高温高压下某些反应的结果在常温常压下无法回复，即没有逆反应)，这与爆破工程相似，即岩矿虽被炸药sw所崩解，而大气压和空气组分在过后一段时间内基本可回复正常——sw有效作用空间内，在事件之后和事件之前的状态已经明显有所不同，但在更大的物质时空范围内，事件的影响效果不明显。总而言之，sw作用的特点是：有时空界限，在时空界限内sw事件几乎改变了一切，但在时空界限外、距离事件中心越久远，受到事件的影响和变化越不明显。sw在介质中高能释放及传播的瞬间，可称为耦合作用。

41、sw与耦合介质的种类和物相状态直接相关。同当量的sw事件在固态和液态、空气和水中，其有效时空界限明显不同，物态的密度、熔点、沸点、比热、黏度、界面张力和流动态等本构特征和应激变化特征，都影响着sw事件的有效时空界限。简言之，sw能态(总能量和释放功率)与作用介质物态，作为“作用”与“反作用”一对矛盾因素，共同决定着有效时空界面及其扩展特征。这种特征属于相对论效应，与牛顿的作用力与反作用力定律相比较，牛顿定律中矛盾双方的“同时性”和“反向性”，对应着sw事件的“延时性”和“扩张～衰减性”，因此牛顿定律已经不足以完全描述和解释冲击波的耦合效应。

42、如果运用微分的思想，随机选取冲击波波阵面的一个点或一个面元，进行受力状态分析，理论上可以把该点或面元所受的暴胀张力与介质对面元产生的反向挤压力进行“平衡态”或者动态分析，这种情况下依旧要利用牛顿运动定律，来建立微分方程。由于实际涉及的变量过多，而核爆能量释放的时间又十分短暂(热中子致核裂变增益链式反应的有效时间不超过0.1毫秒，即10-4s，超过这个时限核材料本身会因热胀蒸发、彻底散逸而使链式核裂变反应终止，如广岛原子弹64kg核燃料实际参与裂变仅有约1kg)，因此在邻近爆点的区域难以建立精确的热力学运动方程，而对于核爆这种量级的sw事件，要么不发生，一旦发生就不可能利用人工技术手段使其中断以避免损失，所有减损手段都只能在躲避、事后补救和预防的范畴内考量，这种情况下，g.i.泰勒的经验公式已经给出了足够启发。因此，从宏观角度看，核爆sw是瞬时高能释放事件；而站在sw本身的能量和时空尺度看，是典型的“短历时、大变形”事件，甚至造成了时空的连续性中断——即从“小时空极高质能密度态(核弹静态，不到1个足球大小)”→极点跃变(引爆：链式反应开始到核裂变结束)→时空“中断(温度和压力在毫秒内以108量级跃升)”→核时空扩张(降维)……，对这类事件实际演变过程的精准理论描述仍在发展和完善。

43、但是，正如泰勒公式给出的启发，通过从结果反推原因，人们早已掌握了核能的和平利用技术，核电已经成为人类的重要能源。与此同时，冲击波sw这种形式的释能事件，也日益受到更多关注。

44、如同和平利用核能一样，随着对sw认识的加深，人们已知除了核爆、地震波、高爆化学品等产生的不可控sw及工程用半可控sw之外，还可以利用电、热、光、机械等多种方式产生可控sw，并已开发出液电、电磁、压电、聚能激光、微爆炸、气动等技术和装置，其效能通过耦合介质的应激反应，实现传导、传播、能量转换和介微结构的改变。比如，医疗用sw能量可以通过人体组织本身作为传导介质到达病灶位置，通过对病灶位置的生物组织的激活效应、对坏死组织的分离效应，而产生治疗作用，也可以利用较强的体外sw脉冲能量达到无创治疗结石的效果。

45、作为机械波，医用sw能在极短的时间内(约10纳秒/ns)达到高峰压(50～100mpa)，周期短(小于10微秒/μs)，能在介质中膨胀和聚焦，从而改变介质的密度，其传播方式是通过介质沿着传播方向交替地压缩和舒张来实现。典型sw波形见图2。

46、高能sw在传播过程中，随着传播介质的可压缩性减小而传播速度加快，高能量与介质相互作用而使波形前沿瞬间变陡，而在波阵面过后又形成一个负压状态，这可称为“截断机制”，即冲击波在介质中形成显著时空界限，超过了界限则质能耦合态自然解体或者过渡到低一级的耦合态，比如由塑性波态转为弹性波态；这种截断机制，决定了冲击波在实物介质中的传播是不连续的单峰波，具有量子化的物理特征。

47、sw波阵面过后形成的负压延迟状态，是冲击波特有的现象，普通声波、超声波和电磁波都没有这种现象，因此负压相可以作为辨别冲击波的一个根本性特征，是冲击波的“指纹密码”。究其本质，可以把冲击波形成阶段看成“形成段”和“解构段”两个部分，比如在一个盛有足量水的容器中放电形成液电冲击波的过程，形成段是水介质吸收冲击能量，但在纳秒(ns)时限内遇到的点源高能释放的能级标度，却超过了点源周边近邻区介质质点晶格结构应变所能吸纳的限度，即参与吸收能量的晶格数目和总容量不足，只能依靠晶格结构解体、带动和撞击更多的晶格来吸收能量，这样就形成了介观～宏观上的“质能耦合态”，达到高峰压，所有参与吸收能量的晶格和质点达到在纳秒时限内的同态化(可以理解为具有相同的振动态)，从而形成一个高能质团局域区；然而对于一个宏观的平衡系统来说，所有破坏的晶格须在微秒时限内回复到平衡态(状态守恒)，于是质能耦合态会自发解构，自然过渡到冲击波的解构段，这一时刻，高压能量已经传递出去，而同态振子回复平衡态需要增加分散自由度，即需要增加动能，这是一个熵增过程，这个熵增过程需要消耗一部分结构势能，而在此微秒级(μs)短暂的时间窗口期内，局域区外的质点来不及向局域区内输送能量，只能依靠局域区内质点晶格自有的内能储备供应本区域的熵增，而内能的消耗则需要势能的填补，势能耗损形成的势阱则表现为负压。这样由于质点的惯性迟滞，无法对冲击波峰压过后形成的势能真空及时填补，就形成了冲击波特有的负压相。由于密度不同，sw的正压段与负压段对应着两种不同的物相特征，而且两种物相密度与介质正常态的密度都不同，因此可以认为冲击波经过的介质经历了两种相反的相变，即晶格压缩到晶格松弛，尽管两段时间不对等。

48、相比之下，普通的声波或超声波都是弹性波，不破坏介质的宏观本构特征，既不存在介质质点振动态及其晶格结构的解构和重组，也不存在传播过程中的局域性质点的熵增和势阱，因此都不存在负压相；电磁波由于光子没有静止质量，没有惯性迟滞，其传播过程也没有负压相；而且，由于没有负压相，也就没有“截断效应”，因此无论普通声波、超声波还是电磁波，都能以连续波形态传播，唯独冲击波必然是单个单个的脉冲传播，这也是“质能耦合”的实际效应之一：冲击波是两种对偶(或互逆)相变的非对称组合态。

49、由于电子的质量极小，其电磁响应速度或振动频率是原子的百倍以上，其惯性迟滞现象极其微弱，同时由于严格地遵循量子化的能级结构，因此电子的波动一般也不显示负压相，由于荷质比(q/m)较质子和原子核大得多而且本身极轻极小，其电场应激反应速度与光速相同，能够通过高频振荡引发的电磁迟滞与晶格相互作用，使导体发生强烈的瞬间电磁热效应而本身消耗的能量极其微弱，故而成为电致冲击波发生的优异载流子体系，是满足包含“固－液相变潜热”需求的冲击波制造的重要基础，特别是对显著质量载荷的宏观物态，大量电子承载的电流潮汐能，几乎是大型可控冲击波发生器的唯一基础性能源。

50、涡旋(vortex)。核爆或堆积化学品猛烈的地表爆炸，在地球的大气层内常见的现象是蘑菇云，而另一伴生现象却往往为人们所忽略：白色气旋，即涡旋环。图3展示了核爆、贝鲁特大爆炸和埃特纳火山喷发瞬间产生的蘑菇云和涡旋环。从产生的时间顺序来看，涡旋环是处于引爆和闪光之后、蘑菇云高升之前和之外，从远处看过去，是先有白色气旋，然后sw开始暴胀——这意味着涡旋环形成的能级较低——随着爆心能量伴随sw猛烈扩张，涡旋环先是远远荡开，然后消散。

51、日常生活中，涡旋或涡环(vortex rings)是一种随处可见、广泛存在于各种物理系统中的环形的特殊结构，这种结构可在流体和气体中传播，例如水流中心或者台风中心的漩涡，甚至吸烟者偶尔从口中喷出的烟圈，都可以作为一个整体在空气中移动，显示出一种独立结构，因此可称其为“孤立子”。在拓扑学中，它与纽结理论密切相关。

52、光学涡旋。在光学系统中也存在涡旋[2]，图4给出了用于产生与表征光学时空涡旋的实验装置(a)以及实验产生的光学涡环的强度等值面(b)和不同切面位置处的涡旋相位分布(c)示意图。

53、光学时空涡环的成功“制造”，在物理学上可以看成是一个现象级事件。它揭示了在宇宙时空中，连光子这种没有静止质量、纯粹表现为能量量子且可以被认为代表最小能量单位、代表最高速度、充满时空的“稀薄”物质(玻色子，自旋为1)，都可以形成涡环态，则可以想象：凡是可流动的、具有吸附力或黏度的有质量的各种物质质点和凝聚态物质，在受到合适的扰动力(能量)情况下，都可以产生涡环——即涡环是一种普遍现象，更进一步而言，涡环是其平面中心发生垂直矢量冲击、将介质向外挤压同时在轴向抽拉带来的结果，或者是其周围发生了向心挤压冲击的结果，是流体介质中的一部分在挤压冲击下的同态翻转效应，类似一个环状弹簧往一根柱体或锥体套装的运动——边平动边翻滚，但不会立即解体，甚至能较长时间存在。特别地，大气中突然出现的涡环往往是冲击波的标志，如火山喷发、高能释放事件等。涡环或涡旋揭示了随处存在的时空曲率，而时空曲率则伴随着引力或斥力，是时空中能量张量的物理表达。

54、降维。如果单纯从能量能级标度的角度看，核爆和sw事件，是高能态时空向低能态时空的降维事件：微小时空中的核力(强相互作用范围为费米fm，约10-15～10-14米)和化学键(约10-12～10-9米,即皮米pm～纳米nm)，由于高能规范场的对称性破缺而释放能量，从四维时空降解到三维空间，在三维空间中以“无穷大”的现象弥漫。降维事件的典型特征是，从奇点(singularity)放出的能量以不可想象的烈度彻底改变了大时空范围内的物理形态(物理学上的奇点特指一个系统中时空无限弯曲或具有无穷阶导数、不能精确描述的那个点)。

55、从物理学规律角度看，牛顿定律适用于三维空间宏观态有显著时间尺度“较慢的运动”描述，但对冲击波的描述则显然失去了精准度，而相对论和量子力学对四维时空结构向三维或准二维转化事件中的物质运动和分布规律的描述更加有效，这种“短历时大变化”都可以看作起源于四维时空中的事件，奇点则是四维向三维或者更低维度映射的发端和通道。拓扑学则是研究这种维度之间变换的有效工具。

56、从拓扑学观点来看，涡旋中心可以认为是各类物理量的奇点，对于二维平面涡旋结构，涡旋中心是一个奇点，也可以称之为一维奇点；相应的，当涡旋中心在三维空间中连接形成直线等空间轨迹，其对应二维奇点；特别地，当涡旋中心形成闭合圆形轨迹，该涡旋结构被称为环形涡旋(toroidal vortices)或涡环。

57、涡旋的拓扑特点，在生活中一个很直观的例子是包饺子之前面皮的制作过程：面粉在加水混和成面团时，是一个没有亏格的球团，手搓球团的每个面点(淀粉分子团簇)在水合氢键作用下，相邻之间发生相互的联结而纤维化，因此整个面团可以视为一个塑性纤维球。从球团中间破开一个孔，即生成了一个亏格，然后一边拉扯一边揉搓，球团很快能随手转变为一个圈环，由于这个圈环之前已经过了成百上千次的反复揉搓挤压变形，上面的每个面点都经历过多次的由内而外、又由外而内扭转，相邻面点之间错位、互绕、互嵌、融合、分离、粘连的复杂运动，如果放在三维空间坐标上看，是一系列连续的点曲率随机变化而成的复杂曲线，因此，面圈环是扭转曲线的组合，也就是一个可塑性涡旋。把这个“涡旋”切断抻直，就是一个长的圆柱体，圆柱体再按等长一段段切断，把每一小段擀成皮，即相当于从三维降解到二维平面。二维平面的饺皮，是从原始的三维球团上取下来的，相当于球团的“切片”，它也是塑性纤维化的，它的纤维比球团的纤维经历了更多的扭转和缠结。

58、声子的能级标度。对纽结的研究，推动了对dna这种双螺旋分子结构的研究。dna的扭曲、绞拧、打结、圈环、方向等等都会影响到dna的复制、转录、重组，进而影响生命活动。dna变形或折叠的尺度，暗示了生物体(生命)所能承受的冲击波的耦合尺度及其强弱标度范围。

59、而对于非生命的物质结构，发生破坏的能级就是一种标度。对晶体结构而言，整个晶格振动系统的哈密顿量为h＝t+u＝∑q0.5(|pq|2+ω2q|qq|2)(1.1)

60、其中pq＝qq称为正则动量。式(1.1)说明，晶格振动的哈密顿量可表述为各独立振动模式即格波的能量之和；而每一个独立振动模式的能量

61、hq＝0.5|pq|2+0.5ω2q|qq|2(1.2)

62、为正则坐标表达的简谐振子的能量。按照量子力学，一个简谐振子的能量本征值为

63、

64、其中nq取0、1、2、…等整数值。晶格振动的能量量子称为声子。晶格振动的总能量表示为

65、

66、晶格振动的能量是量子化的，晶格振动的能量量子称为声子；整个晶格振动的运动状态可用声子气体来描述。声子是玻色子，声子数服从玻色统计室温下声子数与温度t成正比。

67、声子是固体材料中的一个基本的能量量子，对材料的多方面性质都有着重要的影响。热传导现象就是声子运动和相互作用的结果；声子对材料的电阻有重要的影响，金属电阻随温度升高而增大的现象主要就是声子增多、对电子散射增强的结果；声子还在超导现象中扮演着重要的角色，声子与电子相互作用即电声相互作用，使两个电子结合成库珀(coo per)对，从而产生超导现象。

68、经典理论中，由能量均分定理得到，原子的每一个自由度的平均能量是kbt(三维是3个自由度，所以一个原子的平均能量是3kbt)，其中0.5kbt是平均动能，0.5kbt是平均势能；则n个原子构成的三维晶体的内能为

69、e＝3nkbt(1.5)

70、晶格热容量为

71、这是一个与温度无关的常量。式(1.6)的结果称为杜隆-珀替定律。

72、显然，要使固体结构遭到破坏，首先需要在一个预期的断面上把界面上全部的晶格能克服掉，即从外部供给的最低能量量子为e＝3nkbt，若断面上有n个晶格，则最小的破坏能量为ne＝3nnkbt。当冲击波的能量量子足够大、数量足够多时，在波阵面上的n个晶格才会遭到破坏。因此，冲击波脉冲能量量子esw的最小值是3nnkbt，即esw＞3nnkbt。

73、流体的量子能级标度。对流体来说，其晶格结构是不完整的，由于具有自然的流动性，其结构强度只能用界面张力(界面能)σif和黏度ηm这两个指标来表示，冲击波需要具备克服这两个指标的能量量子能级和量子数，才能“破坏”流体的结构。而这种破坏，只能表现为微结构，即纳米到微米的尺寸；至于更大的尺度，属于流体自然具备的对外能量交换状态(环境平衡态)，冲击波多余的能量只能瞬时改变其结构组合，形成一种亚稳的耦合态，随后耦合态解体，组合态解构，流体将以紊流或高压射流方式释放能量。

74、冲击波能量标度。从场效应微分观点看，引入冲击波到流体中形成激波耦合态的条件，是引入到流体中的冲击波能量φ须满足一种物理数学模型，即把冲击波在流体中的作用场，即冲击曲面s，分割成无穷多份，并将每一份的面积记为ds，那么冲击能量通过每一小份的流量dφ作为φ的散度量，可以由能流密度ed与其对应的面积元ds的乘积表示，即dφ＝edds，对散度积分可得所需冲击波的能级强度，在这一模型框架下，流(熔)体中冲击波的能量标度，可以从以下几方面进行下限调控。

75、①当以波在流体中一个等效截面上的能流密度ed表示时，须满足不等式ed＞σaf，式中σaf代表流体中任一位置的面积元内的表面或界面的张力或界面能(单位：牛顿/米n/m或焦耳/平方米j/m2，两个单位是等价的，ed的量纲为mj/mm2，相当于103j/m2，即1mj/mm2＝1000j/m2)。

76、②当以波的传播相速度cp表示时，须满足不等式cp＞σif/ηm，式中σif代表流体的界面张力或界面能(单位：牛顿/米n/m或焦耳/平方米j/m2，两个单位是等价的)，ηm代表流体的动力黏度(单位：牛顿·秒/平方米n·s/m2或帕斯卡秒pa·s，两个单位是等价的)。

77、③当以波在流体中引起的质点拟动速度cn表示时，须满足不等式cn＞(retηm)/(dρm)，式中ret代表流体处于紊流或湍流状态的雷诺数，ηm代表流体的动力黏度，d代表聚焦冲击波形成的焦斑直径(单位：米m)，ρm代表流体密度(单位：千克/立方米kg/m3)；前述质点拟动速度，是指把流体看成牛顿流体，把冲击波压力看成流体驱动力的情景下，以微分视角观察流体体积元质点可以获得的初始瞬时速度，不代表宏观尺度上流体介质的速度。

78、④当以冲击波场在流体中的作用半径r(单位：米m)及该场界面的压力pf表示时，须满足不等式rpf＞σif，式中作用半径r代表冲击波源点或焦点到流体冲击波场界面的距离，σif代表流体的界面张力或界面能。

79、⑤当需要冲击波执行对凝固界面进行重新熔化、使结晶质点重新具备流态化特征，或者使熔体表现为近超流态时，引入的冲击波能级标度选择，应首先考虑熔体合金的热容热e＝3nkbt和熔化潜热lm这两项之和，而后再考虑按上述ed＞σaf、cp＞σif/ηm、cn＞(retηm)/(dρm)、rpf＞σif的一种或几种，进行引入到流体中的冲击波能量φ值的设计，比如φ＞3nkbt+lm+σaf。

80、⑥保障冲击波-介质发生强烈耦合的能量是泰勒经验公式e＝ρcr5/t2，可设φ＞ρd/t2，这里的c是耦合介质的热容比，可通过实验求得；r可以根据需要进行调整，比如需要炮弹打到多远的距离d，按d＝cr5/n进行折算(n取整数)，通过实验得到不同r值对应的d值；其它情况的冲击波可以参照这种模式进行能量设计。

81、冲击波“耦合－解耦”的时间和速度。从前述医用冲击波波形很容易看到，冲击波的正压相和负压相，大致可以看成是与作用介质的耦合态和解耦态，即高能态和低能态；从时间分布来看，解耦的过程可以从升压到降压的转折点开始算起，直到波形回复到正常压力态结束，这个时间段占据了整个冲击波脉冲时间的绝大部分。如果以此为标准看待冲击波的介质耦合与解耦的时间分布状态，显然，解耦时间比耦合时间长得多，大概是耦合时间的数百倍至上千倍；需要注意的是，冲击波波形是从作用介质中一个点的压力变化得到的波形，代表着该点的压力变化速度，但并不代表冲击波本身在介质中的传播速度；作为真实的流体，无论是合金熔体、水溶液、有机溶剂还是导体中的电子电流，都有黏度(电阻和电抗可以认为是电子的运动黏度)，因此作为在介质中传递的波动能量，波动本身的传播速度不可能超过波压变化的速度，即流体中波的传播速度必小于一个波脉冲周期完成的速度，换成时间关系来说，脉冲在介质中移动一个周期相位的时间，必然长于脉冲本身所占用的时间。黏性流体对于在其中运动的动量脉冲结构属于耗散体系，在黏性流体中传播，冲击波能量不可避免地连续损耗，这种损耗对于冲击波的传播速度也是一种连续的迟滞效应，基于冲击波损耗及迟滞，在一定的宏观尺度上即构成能级结构的降维映射，顺从这种降维映射而改变流体介质的外形约束(场约束)，即可使流体介质演变成需要的射流体，或者称之为高动能介质质点群的流体。总之，冲击波解耦时间大于耦合时间2～3个数量级、以及随着传播距离增长而传播速度减小的机制，为降维导控的约束手段的实施创造了条件，也使“导控降维”的方法具有了实际的可行性。图5[3]和图6[4]可以分别表示冲击波在流体介质中的形成段和解体段，即耦合段和解耦段。混沌发展的逻辑映射特性－具有自相似性和分形结构的无穷多个倍周期解，在超过3个周期以后即变得不可预见。

82、冲击波传播的混沌特征(chaos)。高能耦合态对称性破缺后，质点粒子无序性和离散性增加、物质开始进入出现长程序序参量主导表观物性的经典物理学范畴，即“混沌态中的有序性”,符合“离散混沌”的逻辑映射关系式xk+1＝αxk(1-xk)所描述的迭代变化规律，即迭代变化－分叉现象的倍周期规律，如图6。该图形象地揭示了冲击波的“耦合－解耦”在黏性流体中经过3个以上不均匀的周期后对整体质点群系统形成的扰动，其物理意义可以理解为：点源冲击波经过一定的距离后演变为整个系统的压力张量场。

83、涡旋的时空映射(time-space mapping)。维度变换(升维或降维)拓扑的数学方法，一般要用到复变函数中的保角映射(conformal mapping)，这也是实现光学涡环的重要调控手段，它可以实现几何坐标系之间的转换。

84、图7(a)所示，在轨道角动量分选中，保角映射将极坐标系中的涡旋相位映射至直角坐标系中的梯度相位(降维映射)；反之，可以将直角坐标映射至极坐标(升维映射)，而产生光学涡环正是利用了这一点。在二维平面中，保角映射将直线映射为圆，而在三维空间中，其将圆柱面映射为圆环面。图7(b)给出了形成光学涡环的示意图，细长的涡旋管经过空间传播演化形成涡旋环——这可以视为升维映射，因为，如果光涡旋管是相对“无限长”的(光量子数相对无限地增加)，对应的涡旋环直径不需要变大，只要其光子“浓度”增大、或者说光场强度升级，即可以表达这种能量升高效应。图7(c)给出了光学映射过程中需要的变换相位及校正相位。

85、德国数学家霍普夫(heinz hopf)发现了从四维空间的超球面s3到三维空间普通球面s2的“多对一”连续映射，映射的对象称为标量霍普夫子(hopfion)。在几何上，单位球面sn表示n+1维实空间rn+1中与原点距离为1的点的集合。如图8(a)、(b)所示，s1是二维平面中的单位圆，s2是三维空间中的球面，而更高维的球面则很难想象。若要直观地观察高维球面的性质，可以利用空间立体角投影(stereographic projection)来降低维度，从而在可观察的空间中了解高维球面的性质。对于单位圆s1，取圆上的一点并与其他点连线，即可将其投影至一条直线上，如图8(a)所示。类似地，三维球面s2可以投影到二维平面，球面上的纬线被投影至二维平面上的圆，如图8(b)所示。在投影过程中除了投影点外，其他点在投影前后是一一对应的，投影过程也是连续的。

86、对于四维超球面，它将被投影至“整个三维空间(意为三维空间需要多大就可以有多大)”，球面上的纬线将投影至三维空间中的圆环面(外形如救生圈，与救生圈不同的是，圆环面是实心的，而且是环状纤维链绞缠纽结的环簇)，如图8(c)所示。在定义中，四维球面的中轴表示时间轴，即事件从南极点开始，到北极点结束。球面上各维度线对应着三维空间中不同外径的嵌套圆环面，它们都起始于环状奇点——南极点，即当超球面上的纬线逐渐向南极点靠近时，投影空间中的圆环面将逐渐缩小，当纬线移动至南极点时，圆环面将变为一个单位圆，如图8(c)r3中深色圈环线所示；与之相反，当超球面上的纬线逐渐向北极点靠近时，投影空间中的圆环面将逐渐放大，当纬线移动至北极点时，圆环面也展开为一条垂直于单位圆且无限延伸的直线(相当于圆环面变成无穷大后，其空间信息集中压缩/映射到中央的一根时间轴上)。三维空间中无限延伸的直线和单位圆可以看作是圆环面中的奇点结构，它们也可以看作是一个重要的框架，整个三维空间依附于该框架。

87、最近的研究结果表明，基于光学涡环的时空光场可以形成标量光学霍普夫子。光学涡环与其中心穿过的空间涡旋线是标量光学霍普夫子的框架，而光场的相位结构则构成了标量光学霍普夫子结构。如图9(a)所示，高维参量空间中的每个点对应实空间中的一个闭合环，映射关系可用相同的颜色表示。不同的纬线对应不同的圆环面，而圆环面则由一系列闭合环线扭转编织而成。注意到在参量空间中，超球面上的一点经过纬线一周后回到原点，其角坐标φ变化2π，而在光场中2π正好对应相位周期。在标量光学霍普夫子中，其同样包含无限层的圆环面，每层圆环面对应强度等值面。在特定强度等值面上，相位等值线形成一个闭合环，所有相位值的相位等值线构成了相位圆环面。特别地，任意两个不同相位值的等值线会形成霍普夫链，它们相互独立但又相互组合，如图9(b)所示。这种特殊的拓扑结构在几何学上可以表达为：用互不相交的圆和一条直线来填满整个三维空间，每对圆都是成链的，并且直线是穿过圆的。

88、标量光学霍普夫子有两个可控参量，分别为空间涡旋的拓扑荷ls与时空涡环的拓扑荷lt，它们均为正整数。相应的霍普夫不变量则定义为这两个拓扑荷的乘积，因此这样的结构光场具有可调控的拓扑不变量。图9(b)分别给出了霍普夫不变量分别为1和4所对应的光场结构，高阶光学霍普夫子可以形成更为复杂的光学相位结构。

89、在实验上产生标量光学霍普夫子的关键是控制其框架结构，即产生光学涡环及空间涡旋线。实验上仍采用图4(a)所示的实验装置，利用变换相位将涡旋管转化为涡旋环，之后同时施加校正相位及空间涡旋相位，以产生空间涡旋线。可以看出，标量光学霍普夫子的拓扑参量是由两个空间光调制器独立控制的，因此，理论上可以产生任意的环形相位拓扑结构。图9(c)为利用干涉测量法得到的标量光学霍普夫子，其霍普夫不变量为1。

90、光学相位莫比乌斯环(strip)。另一重要的拓扑结构是莫比乌斯环，由德国数学家莫比乌斯(august ferdinand)命名。莫比乌斯环的重要特点是只有一个表面和一个边界，在数学上也称其为不可定向表面。可以很容易地通过扭转并对接一条纸带来演示这样的结构，如图10(a)所示。而在科学研究中，这种拓扑结构可用于构建液晶缺陷，在微腔结构中可以呈现不同的物理性质。实验中可以利用光的偏振特性来产生偏振莫比乌斯环，也可以利用光的相位形成相位莫比乌斯环。

91、相位莫比乌斯环仍来源于超球面的霍普夫纤维化。从标量霍普夫子的例子中可以发现，单一相位纤维仅表示局部空间的性质，而一簇相位纤维则形成完全不同的拓扑结构。不同纤维的集合在整体上可能会表现出完全不同的性质。例如在圆柱形的梳子中，从梳齿可以按圆分为一簇，也可以按线分为一簇。如图10(b)所示，在高维参量空间中选取经线上的点(不同θ角)，它们对应的纤维在实空间形成纽带结构，但各纤维代表的强度值是不等的：距单位圆(时空涡环)越远，强度值越高。在标量霍普夫子中，重点关注了强度等值面上的不同相位等值线，这些等值线以扭转并联方式构成莫比乌斯圆环面，即强度等值面。

92、上面提到可以通过扭转并对接纸带来得到莫比乌斯环，而在时空光场中，光学调控过程也正好对应了物理对接和扭转。时空涡旋管经过光学变换对接为时空涡旋环，而空间涡旋相位则扭转了相位条带。图11(a)给出了拓扑荷为1时，光学涡环的强度等值面及面内的6个相位等值面，可以看到相位等值面形成了条带结构。深色圆环表示涡环轨迹，此时奇点轨迹是相位条带的边界。图11(b)给出了拓扑荷为2时，光学涡环内部的相位条带结构，此时奇点轨迹不再是相位条带的边界而是中轴线，这对形成相位莫比乌斯环十分重要。进一步引入空间涡旋相位，可使相位条带发生扭转，如图11(c)所示。更为清楚地，图11(e)给出了单一相位值形成的相位纽带，其边界分别为涡环的奇点轨迹及相位等值线。实际上，该结构对应于扭转两次形成的环带，不具有单向性。相位纽带的扭转数(twists number)为空间涡旋拓扑荷与时空涡环拓扑荷的商，即ls/lt。在图11(e)所示的结构中，扭转数为1，即扭转360°。为了得到扭转数为半整数的相位莫比乌斯环，需使时空涡环的拓扑荷为2，而空间涡旋的拓扑荷为奇数。图11(d)给出了扭转数为1/2的相位分布，单一相位值形成的相位莫比乌斯环如图11(f)所示，其边界为相位等值线形成的相位纽结。当空间涡旋的拓扑荷阶数增加时，可以形成更为复杂的环面纽结，例如三叶结。

93、不难想象，时空中气态涡旋环内部翻滚但外形保持一定拓扑态的变化运动，其实就是类似于莫比乌斯环带的多拓扑荷扭转态，相当于一种标量霍普夫子，即超球面一个局部的霍普夫纤维化结构，它可以看成是一组纤维不断围绕一条单位圆环轴心绞扭后的结构，每一根纤维都形成一个扭转了的圆环，这些圆环紧密堆积在一起又相互贯穿，在物理和数学的语境中，除了进行纤维的裁断操作外，无论哪一根纤维都无法单独拆取开来。

94、光学涡环的系列研究，详细解析了光学涡环产生过程中的物理机制和光学拓扑结构，深刻揭示了时空光场在时间和空间维度的紧密联系。但对照现实中的高维时空降解为低维时空或者相反的操作，这些研究仍有不完备之处。因为光子或者电磁波调控成为时空光场，是“自外向内”对“弹性介质”进行的拓扑映射，整个过程都是在光子的弹性张量场效应中完成的，犹如篾匠用柳条编筐或者用篾片织席，柳条和篾片都是具有弹韧性的材料。这不同于前述的饺子皮制作，其材料是塑性的，其制作过程由于塑性和粘性，质点运动轨迹的复杂曲折远远超过柳条编筐或篾片织席，自然也不同于光学涡环里的时空光场。换句话说，时空光场的拓扑结构不能完整准确描述饺子皮与面团的拓扑结构。如果拿核爆的时空拓扑结构来比较，则情况更加复杂。比如，如果在爆心附近有一架由角钢焊接制成的方形铁塔，就像输电塔，那么在核爆之后形成的冲击波三维空间发展与时间的关系结构中(四维时空静态坐标为：x2+y2+z2-c2t2,c为光速)，如何还原铁塔的形状(在核爆点附近的高温高压冲击下，铁塔会发生扭曲、熔化乃至汽化，其上质点离散和漂移的范围和轨迹难以跟踪)？用时空光场的拓扑结构显然无法做到这一点，因为时空光场是均匀的，而核爆时空场并不均匀，核爆冲击波时空中的介质至少会有地面与大气之差别，这也是地面核爆产生蘑菇云的原因——球形冲击波被地面反射至空中，实际上在空中显示了核爆能量冲击的“圆锥伞”形貌。

95、由上比较可知，时空光场是一个理想的拓扑结构，是数学家和物理学家对涡环拓扑结构描述的基态。对于三维空间与四维时空的映射问题，时空中的“不均匀”才是常态，而不均匀的具体问题，不可避免地涉及“纽结”问题。

96、纽结(knot)。前述光场涡旋的拓扑解析结构，表明光子或电磁波这种弹性紧致的物质在时空涡旋中，是纤维化的环面纽结结构，而纤维环集结为簇和莫比乌斯环带，每一根纤维都是“首尾”相接的链环，它们堆积起来，在三维空间中显示出刚性的存在。

97、与光场涡旋不同的是，生面团与饺皮之间的拓扑映射，其纤维则是一种塑性结构，可以随意被揉搓捏拉擀制成不同的形状，而其中的淀粉纤维在千变万化之后，可以形成不同的纽结结构；根据复杂程度，纽结可以分成许多的单元结以及它们的组合。图12给出了一些纽结结构的拓扑示意[5]。

98、纽结是日常打结的形式化、标准化与理想化，即一维线条在三维空间中弯弯曲曲所形成的封闭环。在数学中，纽结是自然最本质的形状之一，纽结理论研究的是一种特殊类型的复杂性。而切片纽结(slice knots)让数学家有机会去探究四维空间的奇异性质，在那里二维球面可以被打结，有一些打得非常褶皱，根本无法展平，而切片性则“关联着目前四维拓扑学中最深刻的几个问题”。

99、例如前述核爆点附近的铁塔，在冲击波的四维时空结构中表示冲击波的平均速度]，冲击波对铁塔的作用使铁塔扭曲的形状，在时空四维球面上就会映射出一个纽结形态，如果铁塔需要通过时空反演回复到核爆前的状态，该纽结就代表铁塔在四维时空中运动的“轨迹”。

100、显然，想象在核爆后一个瞬间的照片上，核爆火球的一个表面上发现一个不规则的纽结，如果不事先知晓它本来是什么，单凭一个纽结，是很难还原铁塔形态的；假如有每秒108次以上的快照技术，通过缓慢回放应该是可以确认铁塔是如何在核爆冲击波的作用下快速变化的。这种情况下，三维立体的铁塔要比较准确映射到到四维的时空球面上，等效于拿不同时刻的二维球面分别在四维的时空球面上打结并叠加在一起方可，显然，这种结不能是光滑的，而是一种无法展平、非常褶皱的结，这样才能通过微分解析的方式一步步把纽结还原为铁塔，就像通过缓慢回放快照来解释铁塔如何被冲击波所变化一样。需要注意，铁塔在核爆冲击波作用下的行为，与饺皮原面团在手搓作用下的行为类似，都是塑性纤维，具有松弛性，与光场涡旋中霍普夫纤维的弹性和紧致性是不同的。

101、因此，拓扑学的纽结，在四维时空中的轨迹，可以还原出多种立体架构：纽结纤维的弹性和塑性、紧致和松弛，扭转的次数(结点数)，都是推测其原像物的参数，而每多一个参数就至少多了一种不同还原物。

102、拿地面核爆冲击波的伞锥形，与四维时空的球面标准化模型相比较，可知理论物理学家对四维时空标准化的思路，是将锥形这种实际上开口于无穷边界的形态，转化为球面的封闭形态，而把球的两个极点赋予“始点”与“终点”的意义，从而消除了“无穷大”这种数学上无法处理的情况，进而满足在不同维度之间时空状态的一一对应和映射。

103、膜(membrane/film)和泡(bubble)。按照拓扑的观点，膜和泡，也是一种纽结结构：膜是多个纽结的复合体，是原子～分子尺度的“微曲率旋涡”在一张曲面上的组合，而泡是包裹了一部分气体的膜，是微曲率旋涡在一个二维球面上的组合。

104、如图13，负值应力是两边水介质的压强差以及水合作用力引起的；引力和斥力分布不同，但总体上是平衡的。卵磷脂是一种常见的膜[6]，它有亲油的烃链基团集结面和亲水的脂肪酸基团集结面构成，是一种“双亲分子流体双层膜”，在水溶液中它可以脂肪酸基团的一面向外与水分子以氢键联结，而以烃链基团的一面向内与同样的烃链基团配对联结。从应力分布看，边界基团亲水，与膜的两面水分子之间相互吸引，以及双层膜的烃链分子之间的缠结，都是引力项，为负值，这种引力的合力作用是使双层膜分别向两面弯曲、分离而解体，同时产生向内的挤压作用，致使卵磷脂分子之间由于被弯曲和挤压效应而产生斥力，这种斥力则力图把结构恢复原样，综合的效果是两种作用力平衡，膜的状态也得以稳定。肥皂泡则是一层包裹空气的硬脂酸钠水溶液薄膜封闭球面，其上的长链分子在不解体的状态下可以相对自由地流动。

105、这两种膜结构，本质上都是“双亲分子团”与水分子结合后编织成的纽结集合，在介质中能够独立存在，并以一致的振动态参与热涨落。在一种物质的表面或内部，之所以生成膜结构，必然是由于分子之间形成了界面，界面上的张力高于内部的张力，故而形成膜，如水滴的表面分子层，可以视为膜结构，由于表面张力大，把水滴压缩成球形。

106、流体中与溶剂分子不同界面张力的质点汇聚到一起，如果能够形成相同的振动态，就会集结成一个独立的物相，而如果这个物相宏观上呈现二维态，它就是膜结构；而它们之间汇聚到一起能够成形，成为一个独立结构，则质点之间必然形成某种联结，如果这些联结统一用化学键表达，化学键则可以视为拓扑态下的纤维，质点则可以视为纤维的纽结点；特别地，当质点(分子)之间的键或者纤维可以相对自由地相互交换位置而不产生能量的吸收或释放时，则这种流体属于液晶态。双亲分子流体膜是一种液晶态。

107、对于象卵磷脂、红血球等生物膜而言，它们所形成的面是不对称的，这是由于构成膜的分子的组成不对称、或者是膜两侧的环境不对称，因而造成内在的、呈现高频反复微振动效应的弯曲力，即所谓的自曲(spontaneous curvature)效应，这些特点使得双亲分子膜的弹性和它的热力学运动规律不同于一般的固体薄壳。薄壳力学原理解释不了红血球双凹盘状等细胞形态问题。从数学上来看，弯曲的双亲分子膜可以按“伸张于三维空间中的二维客体”处理，利用这种简单的抽象，理论研究可以归纳为：膜泡的平衡形状满足于一个4阶非线性微分方程。

108、描述生物膜的赫尔弗里希(helfrich)弯曲弹性自由能方程可以写成

109、gc＝(1/2)k(c1+c2－c0)2+k0c1c2

110、的形式，式中gc就是单位面积的弯曲弹性能。c0是描述非对称膜的自曲的曲率常数，它可以是正的也可以是负的。k是弯曲弹性常数，k0是对应于膜面高斯曲率c1c2的弹性模量。与液晶曲率弹性理论相比较可以得出k＝k11t，k11是液晶的展曲弹性常数而t是模的厚度。液晶的展曲常数k11的数量级为10-8达因(10-13n)，而分子长度或分子膜厚度的数量级为10-5cm，因此k的数量级为10-12尔格(10-19j)。许多实验测量都证实了这一点。由于k11和t都是正值，所以弯曲弹性常数k是正值。弹性模量k0与液晶的鞍形展曲常数k24也有类似的关系，因而可正可负，它的数量级也是10-12尔格(10-19j)。

111、泡结构，如肥皂泡，是膜结构的一种特殊形态。吹出的肥皂泡，是肥皂水膜在风力的作用下离开附着的边界同时闭合并包裹了一些空气所致，它的膜的张力与大气压之和，等于其所包裹的气体的压力，泡的体积才能大小平衡；另一方面，肥皂泡膜上的脂肪酸钠分子在膜面上可以相对自由地流动，这种膜其实是一种液晶态。

112、从物理角度看，不论是膜还是泡，都属于一种二维的纽结集成结构，在纤维化之后，总是离不开曲率张量的作用，一旦曲率恒为零(平直化)，纤维变成刚性，不能互绕、缠结和编织，这些拓扑态都无法实现。所以，从根本上说，物质形态的变化是以曲率张量变化为基础的，广义相对论所谓的“物质告诉时空怎样弯曲”不仅适用于宇宙太空，同样适用于微观结构、介观形态和宏观相互作用，相应的，“时空告诉物质如何分布”也适用于所有尺度时空的物理作用。

113、阿波罗尼奥斯垫圆(apollonian gasket)[7]。古希腊数学家阿波罗尼奥斯对相切圆的研究揭示：在平面上给出位置关系没有特别限制的三个圆，用尺规作出第四个圆与已有三个圆都相切的情况共有8种；若限定三个圆两两外切，则第四个圆仅有2种可能性，即与前三圆要么外切(填隙)、要么内切(覆盖)，见图14，全部两两相切的圆最多只有4个，方式为2种。显然，不存在第五个与前四个都两两相切的圆再构成全部相切的关系。

114、如果选择包住三个小圆的大圆，则可以继续用尺规作图实现如下的操作：在大圆内部作出一个圆，使其与平面上已经存在的三个圆相切；该过程显然可以无限持续下去，用越来越小的圆，填充圆与圆之间的空隙。效果如图15，图15为阿波罗尼奥斯垫圆图——无穷级数。

115、由于这些大大小小的圆就像是一个个大轮之间的垫轮，上图里的几何结构被命名为阿波罗尼奥斯垫圆(apollonian gasket)。

116、笛卡尔发现，切点不重合而彼此相切的四个圆的曲率(即圆的半径的倒数)必然满足“所有曲率的平方和等于曲率和的平方的一半”的简单关系。用代数式表示，如果四个彼此相切的圆的曲率分别为a、b、c、d，则上面的定理可以表示成：2(a2+b2+c2+d2)＝(a+b+c+d)2。

117、英国化学家弗雷德里克·索迪于1936年根据这个公式指出，如果最开始的三个相切圆的曲率是整数，则后来所有圆的曲率必然都是整数。这一规律，可以通过计算机程序十分方便地进行任意大数量的垫圆设计，并直观地观察垫圆填充的图案特点和曲率(半径)特征。

118、2023年的暑假期间，美国科罗拉多大学数论专家katherine stange团队的haag和kert zer通过编写计算机程序，以前四个圆的曲率(-23，48，49，52)为底，生成约15000个阿波罗尼奥斯垫圆，如图16。

119、大数量的垫圆图非常直观地显示了“垫圆曲率整数”定律，同时给出了具象丰富的时空物理学和数学示性，部分示性解析如下：

120、1、无限性与收敛性。在一个有限的圆形空间里(称为母圆)，不但等大的圆形无法实现密铺(tiling)，垫圆(相切圆)也无法实现密铺，但全体垫圆的总面积是收敛的，其极大值即大圆的面积。

121、从曲率关系式2(a2+b2+c2+d2)＝(a+b+c+d)2可知：四圆相切的关系可以有无限多的组合，按照同一规则可以在有限的空间里进行无限的细分。

122、如果把圆面积看成能量和能级，与冲击波在流体中传播的混沌效应作比较，则冲击波总能量可以比作母圆面积，各级垫圆可以表示冲击波的解耦降级。

123、2、正负曲率效应。不论垫圆按照怎样的规则进行细分(曲率增大方向)或者粗大化(半径增大方向)的演化，它们都有一个包括一切垫圆成员的母圆，这个母圆是唯一的一个曲率为负值且绝对值最小(即半径最大)的圆，即母圆的面积大于等于全体垫圆的面积之和。因此，从曲率的角度理解垫圆表示的数，可以认为“一个绝对值小的负整数是一切正整数产生的根源”，或者“所有的正整数都起源于一个绝对值更小的负整数”，这与“全体自然数之和等于负的十二分之一(即1+2+3+…+n+…＝-1/12)”的欧拉公式有着深刻的内涵逻辑，这个公式在纯数理逻辑上是悖论，但在几何和物理范域有着强烈的示性意义。

124、圆或者球面，其半径r恒为正值(+/r＞0)，但是，其曲率c却可以在绝对值保持恒定的情况下有正负之分，而且这种分别可以恰好对应一个物理体系的两种截然相反的物理状态：膨胀趋势和收缩趋势，即圆或球处于膨胀状态时，其曲率为正值，处于收缩状态时，其曲率为负值，这样在物理意义上，曲率数值代表一种平衡态，其正负号则代表相互对立的两种趋势，即“涨”和“落”，这正是微观量子振动和自旋效应的最基础的特征。如果曲率为0，则表示一个体系失去了对内外状态的约束力，即体系解体了，或者同化于更大的体系之中，与周围融为一体。

125、同时，垫圆的整体和局部关系，从物理意义上可以有如下的理解或描述：①不论一个有着内部相互作用的质点群具有怎样复杂的相互作用，总是可以找到一个囊括所有这些质点及其相互作用的一种简单背景作用(母圆)，使质点群与其它群分开，并且该简单背景对群内每个质点都起作用，如恒星内核因核聚变导致的热膨胀力与自身的引力作用达到平衡，使恒星成为一个长期稳定的星体，恒星内核物质不会散逸也不会即刻坍缩；②或者可以从曲率控制的意义上理解，从外部对质点群或者体系施加一个压缩作用(负曲率)，能够使这种作用传递到最小的质点，从而导致每个质点都因受到挤压而产生抵抗效应(正曲率)，压力和抗力达到一种平衡态；③或者给出一个更简单形象的实例：容器形状的改变直接影响着流体质点的依存状态；④当流体通过一个压缩的空间(负曲率效应)时内部压力增大(正曲率效应)；⑤一个有限的空间可以无限划分(负曲率效应导致内部产生正曲率效应)，反之，一个含有大量元素(如原子、分子、团簇、流形等微小单元质点)的集群或者体系必有简单的空间边界，即含有大量组元的体系是具有弱可控边际的(系统内部的正曲率效应引发周围的负曲率效应)。

126、大量体系内的组元产生相互作用，必然导致整个体系表现出对应的统计特征，如临界效应、涨落效应、长程序等，其中涨落效应可以视为体系内的平均曲率不变而局部状态处于高速的正负组态交换的动态，这种动态在凝聚态中表现为一种结构力，液态的界面张力和黏度、固态材料的强度，都可以看成质点之间的热涨落、即曲率正负组态交换导致的结构力。

127、3、膜和纽结集成的拓扑态。假设相切圆之切点是固定的，则切点可以看成现实中纽结的拓扑态，一个切点的平均曲率即可用相切2个圆的曲率之和的一半表示，而平均曲率可以直观地表示为纽结的强度。

128、一个母圆中的无数垫圆的切点即可以看成一个给定的时空中可以形成无数的纽结，这时候母圆类似一种膜结构；纽结的实际数量增长的极限，是直到有确定的最大曲率(最小的圆半径)为止。

129、对照生物生存的现实世界的物质基础及人类工业生产的材料基础，在机械运动为主的领域，原子态可以认为是物质世界最大曲率的球体，其次是原子团簇、晶核、晶粒及其各种中间粒度的凝聚态质点，质点越大曲率越小；在电磁运动为主的领域中电子可以认为是具有最大曲率的球体，其次是质子(氢核)、中子、重水原子核(氘核、氚核)、氦核、其它各种原子核，再次是电子的原子轨道、分子轨道、半导体芯片中的晶体管等；而在核爆(聚变或裂变)状态下，夸克(层子)才是曲率最大的质点。总之，作为类球体，所占体积越大曲率越小，而相互作用力越大则曲率越大；在等大的物理球面上，一个质点所受作用力越强则曲率越大，反之则曲率越小。

130、由于材料的机械性能来源于基本粒子之间的引-斥力曲率张量，而粒子的三维立体曲率张量结构十分复杂而难以解析求解，如果把材料转换为二维的膜结构，在二维面(通常可以视为平面)上的质点的曲率结构可以简化为两个对顶锥模型，通过这种转化，使事件变得便于理解和控制。对于宏观膜的厚度在毫米层级，流体基本结构单元最小为原子或离子，最大为纳米态的分子或团簇，最大与最小之间的尺寸等级至少相差106数量级，因此单纯的宏观操作对于单个粒子的平均量子态的影响可以忽略不计，但对于大量的粒子群来说就有可能是显著的，如混合、流速变化、压力变化等。

131、假设相切圆之切点是可以任意滑动的，则垫圆可以看成一个个的涡环(莫比乌斯扭转环)，它们通过切点形成动态但不可切断的纽结，则整个垫圆结构可以看成一个弹性网络的拓扑态，如橡皮筋编织的网兜。

132、4、当第一层级的3个垫圆的曲率半径都相同时(图15)，所生成的垫圆组合整体上具有3次旋转对称性，即外圆每转动2π/3的角度等效于不转动的状态。母圆有三条穿过其中一个垫圆圆心和另两个垫圆切点的直径，这3条直径两两之间的夹角都为π/3。以三条直径中的任意一条为旋转对称轴，把母圆连同内部所有垫圆一起旋转π角度后，所得图像不变，所以该直径可称为翻转对称轴。

133、绕翻转对称轴执行翻转操作后，可以在三维空间得到母球及其内部结构：除母圆和被该翻转轴等分的垫圆成为球体外，其它垫圆均变为圆柱环形面，原来的切点则演变为母圆之球内表面与最大垫圆的圆柱环形面之间的内切圆，或者各相切垫圆的圆柱环形面与圆心处于翻转轴上的球面之外切圆——这种三维结构，与前述四维时空向三维空间的映射关系，具有像似性，即大多数垫圆演变成涡旋环。

134、由上可知，纽结与涡旋(莫比乌斯扭转环)，共同存在(或映射)于阿波罗尼奥斯垫圆的拓扑结构中，纽结可以看成是涡旋的“凝结态”，而涡旋可以看成是翻滚的纽结；膜结构可以看成是纽结的集成态，而分解的膜结构可以散成无数的时空涡环，因此膜结构也可以看成无数涡环的集成态，这与“自旋网络”和“圈量子引力结构”的意义更为接近，从这个意义上，甚至可以认为：物质都是由膜构成的，三维结构是折叠起来的二维膜结构；当能量可以用膜(面)的热涨落进行表达和描述时，三维体积包裹的膜即等价于包裹着能量，三维向二维的解构或者展开，等价于能量在不同维度之间的映射。

135、本发明的原理及有益效果：本发明从分析工业生产的低效能问题入手，从产业链长、作业线长、分工精细繁琐必然带来低效率、高能耗、高成本、难以适应产业竞争和需求变化等的实际问题出发，围绕工业制造和加工的“高能”和“高效”两个核心目标，以“冲击波(sw)高能态”的视角解析凝聚态物质微结构及其运动为主线，在前人取得研究成果和近期实验发生的实际事件的基础上，进行了进一步的关联性分析和逻辑推演，力求创造一种原则性的精简型制造工艺和方法。按行文的顺序，这些研究成果或事件包括：冲击波和耦合效应，涡旋，光学涡旋，降维，声子的能级标度，流体的量子能级标度，冲击波能量标度，冲击波“耦合－解耦”的时间和速度，冲击波传播的混沌特征，涡旋的时空映射，光学相位莫比乌斯环，纽结，膜和泡，阿波罗尼奥斯垫圆等。从这些事件和研究成果的类比中，抽出原则性精简型制造工艺和方法的几个关键环节：高能态(准四维)，降维映射，混沌态，涡旋态射流，工作面。

136、从人类对材料或物质凝聚态的宏观结构期望出发，要求结构材料质地致密、均匀、强韧硬度等机械性能高，功能材料具备所需的功能如导电导热性、磁性能等，同时要求在各种工况环境中良好的适应性，如耐腐蚀性、抗热震性、抗应力腐蚀等。这些要求涉及到晶体的凝固、密铺和密堆、微结构长程有序等方面的控制，一般的工业加工技术建立在冶炼、合金化和机械加工等对材料原子的化学键、分子结构、宏观物性描述等的理论基础上。而宏观控制一般都倾向于简单的线性控制，以牛顿力学为基础。

137、但是，从微观乃至超微观(普朗克尺度10-34j·s或普朗克面积10-70m2)的基础研究出发，物质的微结构和层次结构，是其宏观物性和凝聚态形成的基础，决定着宏观理论及其衍生技术对材料性能的保障能力。

138、从“自旋网络”和“圈量子引力结构”这种普朗克尺度的基础时空结构出发，我们知道时空是量子化的，其质能分布不均匀，是离散型的，但时空量子之间又有自旋波及其相互作用的联系，不是完全的离散。这种结构特点，一直向着“大”尺度、更大尺度的时空结构演进，到原子核、原子、电子的结构层次，体现为基本粒子的自旋、绕旋以及通过自旋和绕旋产生的相互作用来形成关联，从时空的对称性规律和对称性破缺的观点看，微观尺度到宏观尺度，体现了时空及物质对称性的从高到低和“破缺的对称性结构”，如强相互作用、电弱相互作用、引力，其产生的基础都是“自旋网络”和“圈量子引力结构”，符合规范对称性。从最深广的尺度看，是宇宙大爆炸之后不同层级的对称性破缺结构。这种结构的底蕴是非线性、反宏观的，是物质高能态的隐藏结构特征，是物理学研究的“四维时空”，核爆是这种“四维时空”解体的自然体现，而核电和可控核聚变能则是用人类工业制造可以接受的方式，对高能的“四维时空”进行的层级性降解，即降维映射－能量转换。

139、由于微观的“自旋网络”和“圈量子引力结构”决定的物质凝聚态自带的折叠性质，在纳米/纳秒～微米/微秒级尺度上，很难利用已有的技术手段对同级或更小的质点序列进行调控，导致目前人类对材料的性能水平提高或增强的能力基本达到了极限。比如，金属晶体材料的晶粒尺寸平均只能控制在100～200微米，小于50微米就得采用喷射成型、3d打印、强制快冷等特殊加工手段，这些手段的能级标度仍然处于常规水平，即从能量输送上不能渗透到晶格及以下更细小的尺寸水平。

140、材料在结晶时，质点的自旋效应和圈量子引力效应，会引起各种位错和偏析，低能标的宏观技术手段对消除这样的位错和偏析也无能为力。

141、自旋和圈量子，必然涉及到曲率，而从曲率作为时空中的相互作用出发，可以引申出涡旋、莫比乌斯结构、纽结、降维、映射，溯及对原子轨道和原子结构的拓扑，对这些四维时空中的概念及其数理意义和范域的剖析，特别通过“阿波罗尼奥斯垫圆”的丰富示性解析，为对冲击波耦合态的形成和有效利用找到了一种方法论。

142、这种方法论，把冲击波的质点群高能耦合态转变为准二维表面的拓扑映射态，冲击波耦合解构的过程，将同时包含有耦合质点群的高压二维流态化、涡旋态、高速射流、定量排出，这些特征的一体化，从而可以为这种动态的原始态对接多种“接收式”制造和加工工装，依靠质点群自带的动能和涡旋(莫比乌斯扭转态)秩序，解决材料成型和微结构中位错(或非均布位错)、偏析等缺陷问题，使成型的工件微结构致密有序，从而获得更好的综合性能。

143、由此，技术特征“激波耦合场降维导控的工作面”，具有高能、定向、动态可控地传递能量和物质的功能，虽然具有在微观结构演变中“混沌”、难测试的一面，但也避开了现有工业制造流程中“事事精准”的繁琐要求，特别在混沌的过程，由于是耦合介质本身的微观结构决定的一种“近似幂律的自组织临界性”，具有数学上“不发散、不收敛、非周期”和物理宏观尺度上“能量总体守恒但过程中持续损耗转化、近周期的波动传播”的特点，即提供了宏观态的确定性和规律性，使得“从始点到终点”的映射通过“降维法”替代能级变化的描述，使得后续的“对接工装”能够获得确定的结果，这种结果仍然能与初始条件建立严格的对应关系，不但不影响制造或加工效能和结果，反而能够缩短流程和周期，从而得到提高制造加工质量、减少中间环节、节能减排降本增效等效果。尤其值得关注的是，这种功能面跨越了多种制造方式，架起了从宏观到微观一体化制造的桥梁，可以为改进完善现有的工业制造流程和装备提供科学分析的视角和手段。也因为这些优点，“冲击波功能面”可以对应不同技术领域的多种制造装置。

144、保障冲击波-介质发生强烈耦合的能量是泰勒经验公式e＝ρcr5/t2，这是核爆级的高能态，现有的工业生产制造所需的能级一般达不到如此烈度，因此需要根据实际技术领域进行试验检验和调节。

145、比如，对于冲击波直接与液体、即致密的流体的耦合场制造，其最大的便利在于耦合场不用承担物质“固→液相变”的功能，就大大减轻了冲击波负担，这种情况下，冲击波能量φ值的设计，可考虑按前述ed＞σaf、cp＞σif/ηm、cn＞(retηm)/(dρm)、rpf＞σif的一种或几种，进行比较试验，选择最优的冲击波发生源和脉冲能级(各不等式中的符号意义与前文同，即：ed为能流密度、σaf为流体的表面张力，cp为冲击波传播相速度、σif为流体的界面张力、ηm为动力黏度，cn为质点拟动速度、ret为流体雷诺数、ηm为流体动力黏度、d为聚焦冲击波形成的焦斑直径、ρm为流体密度，pf为冲击波场界面的压力、r为场在流体中的作用半径)。

146、对冲击波流体耦合场的降维映射，装置设计为出口为扁平型“狭缝宽面”内腔的、设有流体介质进出口的椭圆半球+双曲线型面倒喇叭状复合壳形型腔的压力容器，可保证冲击波能量通过介质耦合后集中于椭球的第二焦点，为降维映射提供最高能级。将冲击波发生源置于椭圆半球腔体的第一焦点位置，传播的质能耦合体经腔体内表面的反射形成聚焦冲击波，将向椭球的第二焦点汇集，而倒喇叭状的双曲面型腔则为汇集的质能流由准四维的高能态向准二维的束流映射提供了导流面和通道，因为出口为扁平型“狭缝宽面”的通道，即可实现对流体的降维导控，形成有一定的压力、流速和流量的涡旋态脉冲射流，可以对液态环境中的基于化学反应原理的物质合成或者分解，如水溶液、有机溶液、合金熔体的冲击波合成或者进行物质分解，实现制造目的。

147、冲击波脉冲的强扰动可以使流体介质中的各种质点如分子、原子、离子在涡旋态流动中实现充分混合，达到化学反应的高速进行；由于单个的耦合脉冲和解耦效应都是在纳秒～微秒的时间窗口完成的，冲击波的传播和对介质出口扰动过程可以控制在毫秒级的时间窗口内完成，形成延迟脉冲喷射流。压力容器出口处的高压准二维流态化质点群的曲率效应，等价、等效于压力、流速和流量，它的调控，可通过输入的冲击波脉冲能量、工作介质本身耦合所消耗的能量、以及出口形状设计(后续所需保持的喷射流量和速度)来完成，比如，对于某种流体介质，每次喷出1kg的涡旋态流体，需要的冲击波发生源的能量当量，直接通过实验确定后，即不需再改变，制造方式简单高效。

148、有一定质量的毫秒级的脉冲喷射流，在等时间隔的冲击波脉冲源的推动下，如同从高压管路中射出的一波接一波的高压水喷流，既具有很高的动能和势能，又可以随意控制其方向和定量，为液态(湿法)制造提供了高自由度的对接工装。如把1000℃中低温合金(铝合金、镁合金等)的合成和零部件生产连成一个通道直通模具，在压力容器中通过冲击波耦合、波振面扩展扰动、腔壁反射聚焦、倒喇叭曲面的束流导控映射、涡旋的自我搅拌等强烈的微观态混沌、宏观态射流的复杂作用的合金流体介质，带着一定的动能和势能冲向模具，可以实现饱满充型、急速冷却、及时换模、作业持续等高效生产，由于冲击波的高能降维映射、涡旋，合金成分分布更均匀，急速冷却可使工件结晶晶粒细化，提高制造质量，射流脉冲定量准确可提高材料利用率和成材率。又如需要一定压力的水溶液或有机溶液的化学合成或者沉淀结晶，通过这种压力容器中的冲击波效应，能够达到溶质和溶剂的充分混合，提高反应常数，于过程中完成反应，使生成物在出口喷射时占有最大的比例。

149、在椭圆半球+双曲线型面倒喇叭状复合壳形型腔的压力容器中处理液态耦合介质，可以根据生产的需要和制造目的进行制造规模的调整，使出口涡旋态射流成为可与大界面工作面对接，这种大界面可以从平方分米到平方米的范围。比如在进行工业废水的处理，工业废渣的水循环处理等，把药剂/废水或者水/废渣/药剂按比例随脉冲间隔从入口送进冲击波处理容器，由于经历常规处理没有的高压涡旋环节，混合液反应更彻底，或者使常压下不能进行的反应能够有效进行，即可实现高效的处理。

150、对于需要先经历“固→液相变”再完成制造加工作业的情况，冲击波制造与前述可以大界面工作面处理液体的情况不同。必须选择高能态的电脉冲或光脉冲(高能激光)作为高能耦合场的物质载体，而且只能以平方毫米至平方厘米级的小界面工作面进行制造加工，但同时由于小界面工作面相变的瞬时性和涡旋射流几乎与熔化同时发生，使得制造方式可以充分依靠小截面固态材料的承载能力完成降维映射所需的支撑载体，而不必再为冲击波耦合场设置专门的容器型腔。

151、从更广的意义而言，对于使用高压、强电流脉冲进行导体介质界面质点群耦合的情况，这种“封闭型容器”就是导体线材/丝材本身，通过电压电流和临界距离伸缩频率的调控，使耦合质点群满足所需的流态化、涡旋态、射流和流量的动态平衡，并支撑起“焊接/堆积式增材制造与导体线材/丝材连续耗用的平衡”这样一种新型增材制造方式。同理，在超冷真空状态下利用高能超短激光脉冲对原子气中的质点——单个原子进行耦合并定向射流到磁光阱中，建设人们需要的新型原子群态结构和以此为基元的新材料，这一过程需要在真空冷室中才能实现，则真空冷室也可以看成一种广义的“封闭型容器”。这就是“基于膜曲率调控的激波耦合拓扑模型”的基本功能。

152、更为简要地说，“冲击波赋能的可控流态化工作介质”，是“基于膜曲率调控的激波耦合拓扑模型/基于激波耦合场降维导控的工作面”的核心功能和价值，这种模型由于简练易懂，因而具有广义性，超越了多种具体的机械结构(如压力容器、冲击波源、铸造工装、搅拌装置等)的限制，可以涵盖和推广到多种形式和方式的合成、制造、加工的原型工艺机制。

153、本发明中列举了如下的工业生产或实验用原型机构：

154、枪击式的喷流涡旋与模具容器对接；

155、丝材电弧增材制造(waam)；

156、激光单原子组合制造；

157、大型金属制品的沿大平面精准剖解的切割加工；

158、高速铣磨刃具对切割形成的大面进行精密铣磨；

159、固态(异质)材料的焊接(搅拌摩擦焊)；

160、进行温度条件不太高(如1000℃以下)的铝合金熔体、镁合金熔体的合金熔体生产或进一步的射流成型；

161、进行大量的有压力、温度条件的有机合成或生产各种配合物。

162、综上，利用可控激波造成的高能脉冲与物质质点的强耦合效应和解耦合作用，控制其膜态化曲率(压力、速度、流量等)，能够实现高效的制造和加工，获得常规手段无法做到或很难做到的超常效果。