一种基于渠道自平衡特性的闸门实时优化调控方法

本发明属于明渠调水工程自动化调控领域，具体涉及一种基于渠道自平衡特性的闸门实时优化调控方法。

背景技术：

1、明渠输水系统各建筑物之间水力联系紧密，存在非线性、大时滞以及多扰动的特性，输水过程中伴随着复杂的水力响应过程,任何扰动都可能会导致局部或整个输水系统状态的变化，给工程调控带来巨大的挑战。

2、尽管现有工程大多具有完备的远程闸控系统和实时水情监测系统，但由于我国对于输水渠道自动化的研究起步较晚，渠道自动化技术的工程应用较少，关于渠道闸门自动化控制技术暂不成熟，目前绝大多数工程仍然处于依靠人力主观经验进行简单逻辑控制的阶段，工作强度大、决策效率低，可能会因为决策不当导致产生工程安全问题。

3、针对以上问题，我们提出了一种考虑明渠调水系统实时运行时面临不同扰动工况下，优化闸门实时运行调控次数的方法。

4、对于如何优化明渠调水工程闸门实时运行调控次数，相关文献报道较为缺乏，已有的方法技术无法有效为优化闸门实时运行调控次数提供技术支撑。

技术实现思路

1、本发明的目的在于提供一种基于渠道自平衡特性的闸门实时优化调控方法，从而解决现有技术中存在的前述问题。

2、为了实现上述目的，本发明采用的技术方案如下：

3、一种基于渠道自平衡特性的闸门实时优化调控方法，包括如下步骤，

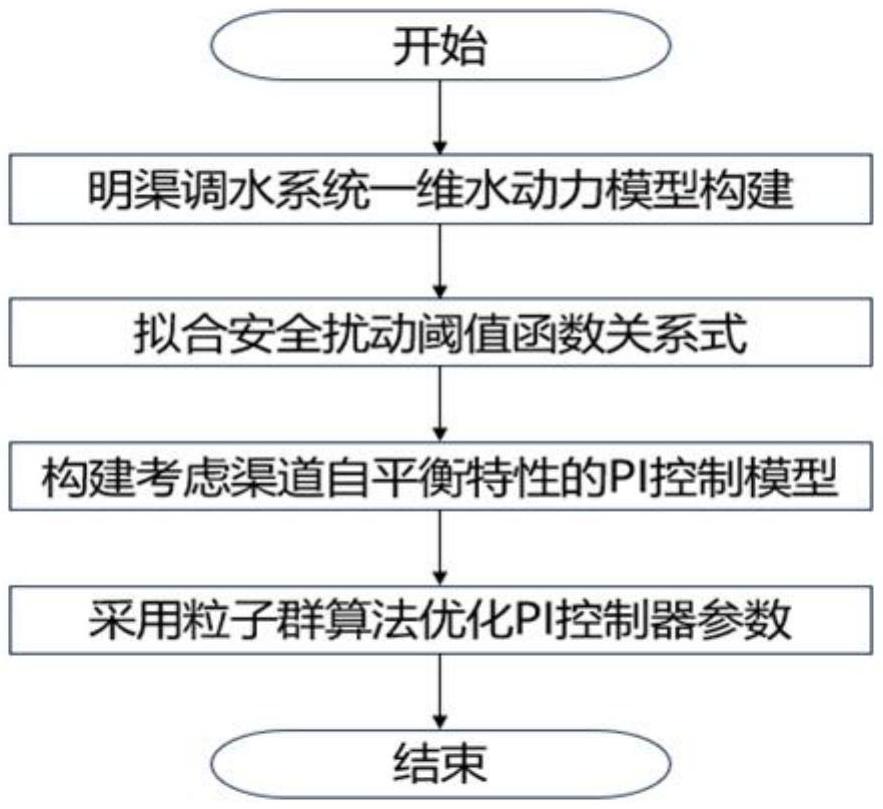
4、s1、明渠调水系统一维水动力模型构建；

5、基于圣维南方程组，构建明渠调水系统一维水动力模型，采用追赶法求解模型，同时对不同水工建筑物水力参数进行率定，以提升模型模拟精度。

6、s2、渠道安全扰动阈值函数关系提炼；

7、基于一维水动力模型，将模型的内外边界范围进行分区设计不同的工况，施加不同的扰动值。考虑渠道的自平衡特性，以工程运行水位限制与变幅为约束条件筛选合理的安全扰动阈值，并与初始流量以及闸门开度进行双变量公式拟合。

8、s3、考虑渠道自平衡特性的pi控制模型构建；

9、基于传统的pid控制方程进行离散并生成增量式pid控制表达式，适用于渠道的闸前常水位控制。考虑渠道自平衡特性，以渠道安全扰动阈值为触发条件，构建pi控制模型。

10、s4、基于粒子群算法的pi控制器参数优化；

11、针对pi控制器中kp和ti参数在不同工况下表现不一致，采用粒子群算法进行参数优化，使pi控制器在不同工况下达到最优控制效果，生成扰动工况下的闸门调控过程。

12、进一步地，步骤s1具体为，

13、基于圣维南方程组，并对典型建筑物进行概化来构建明渠调水工程一维水动力模型，同时对糙率和过闸流量系数等水力参数进行率定，采用追赶法进行求解。本发明不限制水力参数率定方法，常用的方法包括经验公式法、参数反演法等。

14、进一步地，步骤s2具体为，

15、s21、基于一维水动力模型，以渠池下游设计水位、上游来水流量、分水口分水流量作为外边界，以闸门的开度作为内边界，并对内外边界的范围进行分区设计不同的工况；

16、s22、对渠道上游初始流量或分水口分水流量施加不同的扰动值，考虑渠道的自平衡特性并以工程设计运行水位限制与变幅为约束条件，筛选合理安全扰动阈值，水位运行限制约束公式如下：

17、|zmax-zm|≤0.03m

18、|zmin-zm|≤0.03m

19、水位变幅约束公式如下：

20、|δh1小时|≤15cm

21、|δh24小时|≤30cm

22、式中：zm为模拟稳定水位，zmax为渠道最高运行水位(根据初始稳定水位与水位允许变幅求得，且zmax＜水位上限)，zmin为渠道最低运行水位(根据初始稳定水位与水位允许变幅求得，zmin＞水位下限),0.03m视为模型模拟误差允许范围；δh1小时表示每小时的水位变化，δh24小时表示每24小时的水位变化。

23、s23、将渠道水力安全扰动阈值与初始流量以及闸门开度进行双变量公式拟合，实现不同工况下安全扰动阈值的快速计算；

24、进一步地，步骤s3具体为，

25、s31、基于传统的pid控制理论，建立适用明渠调水系统闸前常水位控制的增量式pid控制公式。经典的pid控制方程公式如下：

26、

27、式中，u(t)为控制器在t时刻的输出；kp为比例系数；ti为积分时间；td为微分时间；e(t)为误差信号。

28、pid控制实际应用是根据采样的系统值和控制值的偏差来对系统进行控制，在数字系统中进行pid算法控制，需要对上述算法进行离散化，当采样周期t足够小时，可以做如下近似：

29、u(t)≈u(k

30、e(t)≈e(k)

31、

32、式中，t为采样周期，k为采样序号，e(k)-e(k-1)为不同时间被控量与控制目标的差值，用这种近似方法，可以得到数字pid控制算法离散后的表达式：

33、

34、将上述各项取增量，得到增量式pid控制表达式如下：

35、

36、式中，δu(k)＝u(k)-u(k-1)，δe(k)＝e(k)-e(k-1)，k为采样序号。

37、s32、基于扰动阈值计算结果设计一种控制模型的触发机制：当扰动或一定时间内的叠加扰动处于安全调控阈值范围内，无需触发模型对闸门进行控制，此时闸前水位可以通过自平衡特性稳定在水位安全限制以内；当扰动或一定时间内的叠加扰动超出安全调控阈值范围，则判断为仅通过自平衡特性无法将水位稳定在安全限制以内，未来闸前水位将超限，此时需要触发控制模型对闸门开度进行调整，使水位重新回到目标水位附近。

38、由于微分控制在时滞系统中的作用效果不佳，微分项的调控极易引起水位的频繁波动,因此微分参数为0，则pi控制算法表达式为：

39、

40、式中，δu(k)为控制器在第k个时刻的控制输出增量；e(k)当前时刻误差信号；δe(k)为误差增量；kp为比例系数；ti为积分时间；t为采样周期。

41、以模拟的节制闸闸前水位作为被控变量，闸门开度作为控制变量，构建考虑渠道自平衡特性的pi控制模型。

42、进一步地，步骤s4具体为，

43、在对参数进行优化时,令种群中粒子数为s,以kp和ti,作为不同粒子的坐标记为x(i,t),初始种群可以根据经验在允许范围内取值，同时每个粒子都存在一定的速度v(i,t)，其中i表示粒子编号，t表示迭代次数。首先在一个范围内随机生成不同粒子的初始坐标和初始速度。再使用模拟模型计算得到对应工况下的自动控制结果，通过构造适应度函数评价不同kp和ti,的优劣。适应度函数如下:

44、minδz＝max|zi-zt|

45、式中，δz为需要最小化的目标函数，zi为每时刻的水位值，zt为目标水位值。

46、对每个粒子坐标进行评价后统计得到其所经过的坐标中最优的一组，称为个体最优坐标，计为pbest(i)，在每一代的计算中统计得到所有粒子中最优的一组成为群体最优坐标，计为gbest。其中每一代粒子的速度和位置更新公式如下:

47、v(i,t+1)＝wv(i,t)+c1r1(pbest(i)-x(i,t))+c2r2(gbest-x(i,t))

48、x(i,t+1)＝x(i,t)+v(i,t+1)

49、式中，w为惯性因子；c1和c2称为学习因子或加速因子；r1和r2为分布于[0,1]的随机数。

50、与现有技术相比，本发明具有以下优点：

51、1、本发明构建了考虑渠道自平衡特性的pi控制模型，减少了闸门实时调控过程。

52、2、本发明引入粒子群算法，对pi控制器参数实时优化，提高了模型的适应度，更适用实际工程。

53、3、本发明所述方法为一套固定的程序，只需输入历史监测数据以及约束条件，便可自动生成闸门调控过程。