基于分布式模型预测控制的客货共线列车协同驾驶策略优化方法

本发明涉及智能交通，具体是一种基于分布式模型预测控制的客货共线列车协同驾驶策略在线优化方法。

背景技术：

1、铁路交通由于其交通能力大、能耗低、效率高，在公共交通系统中变得越来越重要。列车自动运行(ato)系统是列车控制系统的关键组成部分，可以实现列车运行的自动控制和调整，降低驾驶员劳动强度，降低运行能耗，确保运行系统的安全和可靠性。近几十年来，人们提出了大量先进的ato控制算法，以实现精确、快速和稳定的跟踪控制，以应对不断扩大的铁路网和提高的列车速度。

2、在列车离开车站之前，ato系统计算出下一次行程的推荐速度曲线，它作为ato系统的参考信号，并确定计划的位置和给定时间内的运行速度。它在确保列车自动运行过程中的准时性和能源效率方面起着至关重要的作用。推荐速度曲线的生成通常被建模为一个优化问题，可以通过多种计算方法来求解。这些方法大致可以分为两类：直接方法和间接方法。间接法，如庞特里亚金极大值原理，已被广泛应用于列车最优控制问题。最早关于基于庞特里亚金极大值原理的列车最优控制问题的工作是1968年由ichikawa进行研究的，其中导出了列车在水平轨道上节能行驶的最优机制(即最大加速、巡航、惰行和最大制动)。此后，许多研究人员利用庞特里亚金极大值原理，在考虑轨道坡度变化、任意速度限制和牵引力/制动力约束的情况下，生成最优的列车驾驶策略和速度曲线。上述这些间接方法的主要挑战之一是得到最优机制转换条件。相比之下，直接方法是通过使用数学规划算法来寻找原始最优问题的近似解。近年来，伪谱法由于其较快的收敛速度和较好的计算精度，被普遍用于求解列车最优控制问题。本发明针对单线线路提出了一种新的多列车轨迹优化方法，旨在找到节省能耗的最优速度曲线。

3、然而，许多方法大多局限于固定的运行参数，如列车阻力系数、线路静态限速等，离线计算列车的参考速度曲线。如果某列车的ato系统在存在列车运行干扰的情况下仍然按照离线确定的参考曲线运行，可能会造成不必要的能量消耗，甚至导致整条线路的混乱。不仅如此，为支持区域经济增长，提升铁路在货运方面的竞争力，部分铁路积极推行客货混跑模式，客货列车共线运营。显然，客货列车在运营需求和制约因素上存在显著差异，给交通调控和管理带来了挑战。然而，现有关于客货共线列车优化控制问题的研究工作仍十分有限。

4、现有的技术文献[1]([1]li,d.,dong,x.,cao,j.,zhang,s.,and yang,l.(2022).“energy-efficient rail transit vertical alignment optimization:gaussianpseudospectral method.”journal of transportation engineering,part a.systems,(1),148.)提出了以能耗和运行时间偏差最小为目标的高能效线路垂直对准优化模型，并提出了精确求解的方法。

5、现有的技术文献[2]([2]yan,x.-h.,cai,b.-g.,ning,b.,and shangguan,w.(2015).“moving horizon optimization of dynamic trajectory planning for high-speed train operation.”ieee transactions on intelligent transportationsystems,17(5),1258–1270.)提出了一种滚动时域优化方案，用以处理多个高速列车的协同运行规划问题，较大程度上优化了不确定条件下多列车的参考轨迹。

6、现有的技术文献[3]([3]liu,l.and dessouky,m.(2017).“a decompositionbased hybrid heuristic algorithm for the joint passenger and freight trainscheduling problem.”computers&operations research,87,165–182.)研究了面向复杂铁路网络的客货列车联合调度问题，并提出了一种新颖的启发式算法，但是并没有考虑到节能和列车运行过程中受到的干扰。

7、综上，目前针对客货共线运行场景，还没有一种考虑到运行扰动并且兼顾节能运行的客货共线列车在线控制算法。

技术实现思路

1、基于此，本发明的目的是提供一种新的列车运行在线控制算法，采用分布式模型预测控制(dmpc)方法设计考虑运行扰动的客货共线列车节能运行在线控制算法。

2、为达到上述目的，本发明提供了如下技术方案：

3、基于分布式模型预测控制的客货共线列车协同驾驶策略优化方法，包括以下步骤

4、步骤1：建立基本列车动力学模型；

5、步骤1.1：旅客列车在各个车站都停靠，货运列车不在中间站停靠。令qt＝qp∪qf，其中qt表示列车的集合，qp表示旅客列车的集合，qf表示货运列车的集合。则对于列车i∈qt以位置s为自变量的动力学模型描述为：

6、

7、其中，vi(s)为列车i的速度，ti为时间，s为位置，mi为列车i的质量，ui1(s)和ui2(s)分别表示列车i的牵引力和制动力。货运列车的最大牵引力和最大制动力均大于客运列车的最大牵引力和最大制动力，两者具有不同的牵引特性曲线。是由机械和空气摩擦引起的列车运行基本阻力，一般由以下davis方程表示：

8、

9、其中，ai、bi、ci为由特定列车决定的非负系数。此外，是由轨道坡度引起的线路阻力，可表示为：

10、

11、其中，α(s)为轨道在位置s处的倾斜角，g为重力加速度。当α(s)较小时，公式(3)成立。

12、由于复杂的环境因素，列车在运行过程中不可避免地会受到外界的干扰，即：

13、

14、其中，rand表示使用rand函数生成的一组随机数，模拟列车运行时受到的干扰。

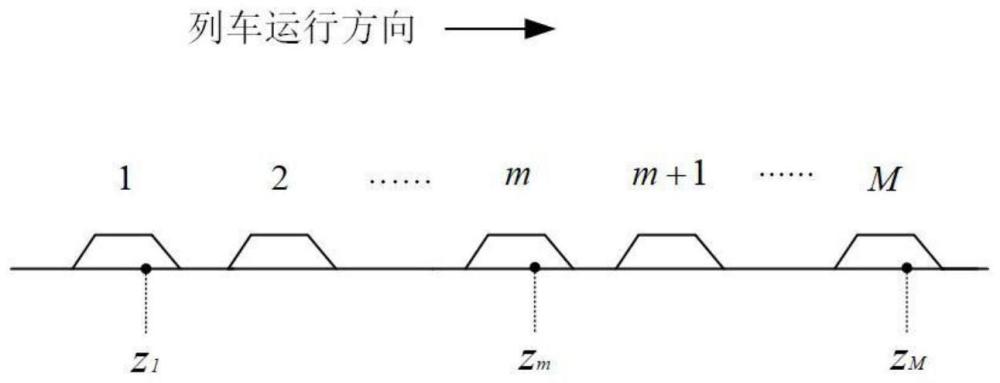
15、步骤1.2：单线铁路线路图如图1所示，其中，车站总数为m，令zm，m＝1,2,…,m表示车站m的位置，则列车运行的初始位置为z1，终点位置为zm。

16、步骤2：设计列车运行控制目标；

17、步骤2.1：对于旅客列车i∈qp，时刻表指定了每列车的规定到站和发车时刻，每列车必须在给定时刻离开初始位置z1，然后沿轨道运行，在给定时刻到达终点位置zm。

18、因此，

19、

20、此外，旅客列车在中间站需要停靠，便于旅客在中间站上下车：

21、vi(zm)＝0，m＝2,3,...,m-1    (6)

22、

23、

24、其中zm为车站m的位置，为列车i在车站m的实际到达时间，为列车i在车站m的实际出发时间，为列车i在车站m的规定到达时间，为列车i在车站m的规定出发时间。

25、步骤2.2：定义列车运行过程中的各项约束。

26、在列车运行过程中，需要考虑如下的牵引力和制动力约束、速度约束和列车间距约束：

27、

28、

29、0≤vi(s)vmax(s)    (11)

30、ti(s)-ti-1(s)≥tmin    (12)

31、其中，和分别为最大牵引力和最大制动力，vmax(s)为列车在位置s处的限速值，tmin表示列车运行的最小安全间距。

32、旅客列车i∈qp遵循约束条件(5)-(12)。对于货物列车i∈qf，它在始发站和终点站遵循与旅客列车相同的约束条件，同时直接通过中间车站而不进行任何停靠。货物列车与旅客列车受到相同的运行约束，因此，货物列车遵循约束条件(5)，约束条件(9)-(12)。

33、步骤2.3：建立旅客列车的控制目标函数。

34、对于旅客列车i∈qp，控制目标是最小化列车在各个站间运行时消耗的牵引能耗：

35、

36、步骤2.4：建立货物列车的控制目标函数。

37、对于货物列车i∈qf，控制目标是最小化列车的总运行时间和总牵引能耗：

38、

39、式中：wif为权重系数。

40、步骤3：设计局部优化问题。

41、步骤3.1：搭建列车轨迹优化的分布式控制框架。

42、每列车都是自主控制，并且具有计算和与其他列车通信的能力。本发明使用如图2所示的领导者-跟随者拓扑结构来模拟单线铁路上客货共线列车之间的通信。具体来说，列车i只能接收来自列车i-1的信息，而列车1不接收来自其他列车的信息。其中，窗口表示旅客列车和货运列车。

43、步骤3.2：建立局部优化问题。

44、为不同种列车分配一个优化问题。本发明将采用分布式模型预测控制方法(dmpc)为每列车在等式(1)中设计控制律ui1(s)和ui2(s)。

45、列车节能控制问题归结为以列车速度和时间为状态变量，以牵引力和制动力为控制变量的一般最优控制问题。令xi(s)＝[vi(s)，ti(s)]t，ui(s)＝[ui1(s)，ui2(s)]t。将公式(1)改写成如下的紧凑形式：

46、

47、对于旅客列车，考虑内的列车优化控制问题，其中si为列车i当前位置，为沿运行方向下一车站ni的位置。在预测时域内，第k步旅客列车节能控制问题的代价函数可以写为：

48、

49、优化问题的初始条件为xi(si)＝[vi(si)，ti(si)]，表示列车i在当前位置si的速度和时间。在预测时域的最后，终端状态需要满足：

50、

51、其中，为下一站ni的位置，为列车i在下一站ni的规定到达时间，ta为列车到站时间的允许偏差值。为了避免发生碰撞，必须满足安全约束：

52、

53、其中，是由列车i-1在k-1步计算得到的预测时间序列，tmin表示列车运行的最小安全时间间隔。在预测时域内，第k步旅客列车的节能控制问题可以表述为：

54、

55、其中，表示旅客列车的最大限速值。

56、对于货运列车，考虑[si，zm]内的最优列车控制问题，第k步列车节能控制问题的代价函数为：

57、

58、在预测时域的最后，终端状态需要满足：

59、

60、在预测时域[si，zm]内，第k步货物列车的节能控制问题表述为：

61、

62、其中，表示货物列车的最大限速值。

63、在优化问题(21)和(24)中，在当前位置si测量到实时状态xi(si)＝[vi(si)，ti(si)]。通过求解问题(21)或(24)可以得到预测时域内的最优控制序列而且列车只执行第一个控制量在下一个采样时刻tk+1中，用更新的列车状态重新求解最优控制问题(21)和(24)，并且只让列车执行第一个控制量。通过滚动时域重复求解一组最优控制问题，解决基于列车运行状态实时更新的列车在线控制问题。

64、步骤4：设计客货共线列车节能协同控制dmpc算法。

65、步骤4.1：每列车通过求解一个包含其自身和邻居信息的局部优化问题(21)或(24)得到其控制输入，具体步骤见dmpc算法：

66、dmpc算法输入：各车站的位置zm，实时测量的列车i在tk时刻的状态[vi(si)，ti(si)]，其中ti(si)＝tk，各列车在车站m的规定到达时间和规定发车时间

67、dmpc算法输出：预测时域内的预测状态轨迹和最优控制序列。

68、第1步，令k＝0，i车测量tk时刻的状态[vi(si)，ti，(si)]，求解局部优化问题(21)或(24)，得到和并更新之前存储的预测状态轨迹和

69、第2步，i车传送其更新的预测状态轨迹给后车。

70、第3步，i车执行最优控制量

71、第4步，令k＝k+1，转第1步。

72、本发明的一种基于分布式模型预测控制的客货共线列车协同驾驶策略优化方法，较现有技术而言，具有如下优点及功效：(1)针对客运列车和货运列车不同的运营需求，分别设计了客运列车和货运列车的控制目标、约束条件和节能优化问题。(2)通过对每一步列车节能优化控制问题的反复求解，可以在线得到动态运行条件下列车全程的节能速度轨迹。(3)提出的算法可以同时对宏观层面的列车运行图和微观层面的列车控制策略进行优化调整，实现了列车运行速度的精确控制。