一种基于无迹卡尔曼滤波器的路感反馈力矩估算方法

本发明涉及车辆的线控底盘领域，尤其是一种基于无迹卡尔曼滤波器的路感反馈力矩估算方法。

背景技术：

1、线控转向系统作为新一代转向系统，与机械转向系统的差异较大，线控转向系统去掉了转向柱，在转向盘与车轮之间没有直接的机械连接，因此线控转向系统具有布置灵活度更高，安全性更高、可变传动比、路感可任意设计的优点。但由于系统转向盘与车轮之间缺少直接的机械连接，导致驾驶员通过sbw系统的转向盘不能像传统转向系统那样直接感受到路面的反馈。而驾驶员需要通过转向盘路感获得路面状况以及车身状态，以保障行车安全，因此有必要通过电机等装置模拟真实的路感。

2、如今的线控转向系统路感反馈主要分为两种，分别为动力学模型法以及参数拟合法。

3、参考cn117068259a、cn114954640a，动力学模型法的原理则是通过建立模型，利用目前汽车流行的转矩转角传感器、车速传感器等设备获取的数值作为输入，直接计算得到路感反馈力矩。这种方法不用再加装额外传感器，成本较低，且获得的路感反馈力矩值与传统汽车接近，驾驶员能够很快适应。但是，这种方法需要获得轮胎拖距、轮胎载荷等实时变化的参数，而这些参数的动态变化数值较难得到，若是采用定值的轮胎拖距、轮胎载荷等参数，又将导致计算得到的路感反馈力矩不准确，无法获得真实的路感。

4、参考cn110509983a，参数拟合法是一种利用函数拟合、神经网络等方式拟合出路感反馈力矩的方法。这种方式也不需要加装传感器，只需要利用现有传感器获得的数值判断应该输出的路感反馈力矩值。但缺点是这种方法同样不能很好地反映真实的路感。

技术实现思路

1、本发明的目的在于提供一种基于无迹卡尔曼滤波器的路感反馈力矩估算方法，用以解决动力学模型法轮胎拖距、轮胎载荷等参数获取困难，以及参数拟合法由于没有获得实际路感信息而不能很好地反映真实的路感的问题。

2、为实现上述目的，采用以下技术方案：

3、一种基于无迹卡尔曼滤波器的路感反馈力矩估算方法，包括以下步骤：

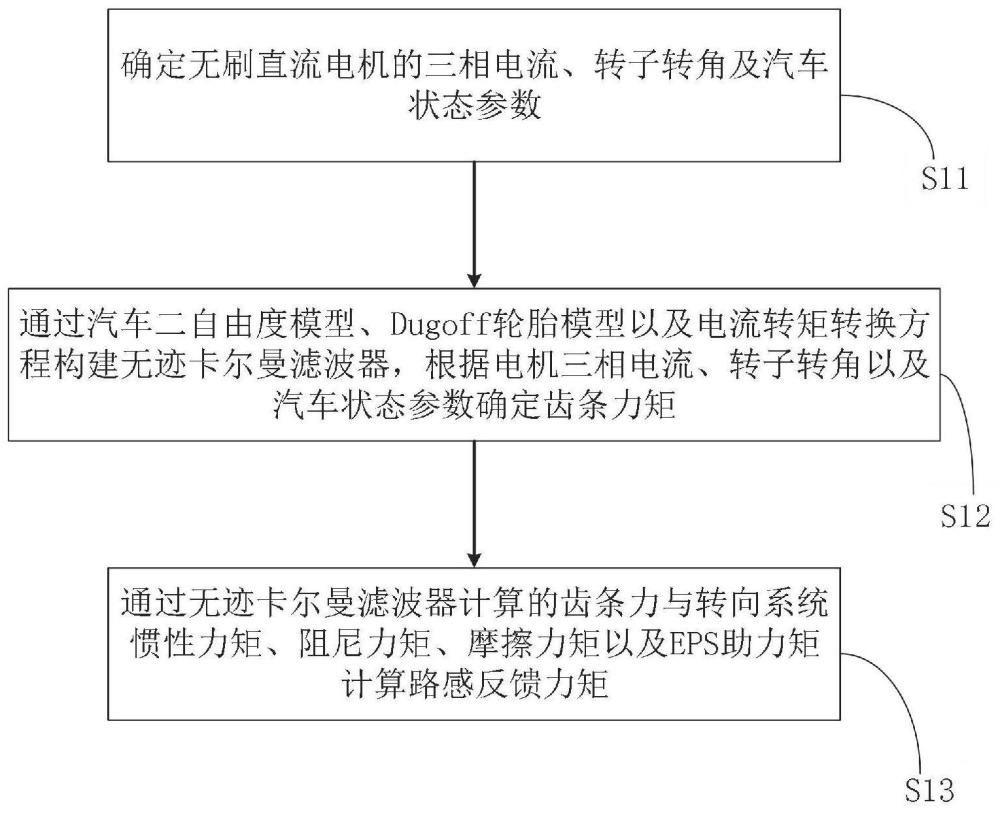
4、获取无刷直流电机的三相电流、转子转角及汽车状态参数；

5、通过汽车二自由度模型、dugoff轮胎模型以及电流转矩转换方程构建无迹卡尔曼滤波器，根据电机的三相电流、转子转角以及汽车状态参数确定齿条力矩；

6、根据汽车状态参数计算转向系统的惯性力矩、阻尼力矩、摩擦力矩以及eps助力矩；

7、通过无迹卡尔曼滤波器计算的齿条力矩，与所计算的惯性力矩、阻尼力矩、摩擦力矩以及eps助力矩，计算路感反馈力矩。

8、进一步的，无迹卡尔曼滤波器的构建具体为：

9、步骤s1：将无刷直流电机的三相电流以及转子转角的数值传输给无迹卡尔曼滤波器的观测方程，观测方程为无刷直流电机的电流转矩转换方程，观测变量为：

10、式中，ia、ib、ic分别为无刷直流电机a、b、c相电流，θr为当前电机转子转角；

11、将汽车运动过程中的前轮转角以及车速的数值传输给无迹卡尔曼滤波器的系统状态方程，无迹卡尔曼滤波器系统状态方程包括dugoff轮胎模型、二自由度模型；

12、无迹卡尔曼滤波器状态变量为：

13、式中，vy为侧向车速，ωr为横摆角速度，fy为为轮胎侧向力，tr’为无迹卡尔曼滤波的状态齿条力矩。

14、步骤s2：无迹卡尔曼滤波器根据无迹变换得到k时刻sigma点集：

15、

16、式中：表示k时刻的状态变量；p(k|k)表示k时刻的协方差矩阵；ε表示缩放比例参数；i＝表示第几个sigma点；n表示状态变量维数；

17、步骤s3：根据无迹卡尔曼滤波器状态变量预测值计算公式，得到一组代表这组变量高斯分布的采样点x(i)(k+1|k)，其公式为：

18、x(i)(k+1|k)＝f[k，x(i)(k|k)]

19、式中：f[k，x(i)(k|k)]表示在k时刻，将x(i)(k|k)代入到无迹卡尔曼滤波器系统状态方程的二自由度模型、dugoff轮胎模型、状态变量预测值计算公式中计算。

20、步骤s4：进一步预测得到的状态变量的期望，将其作为k+1时刻状态变量的估计值，其公式为：

21、

22、式中：ω(i)表示第i个sigma点权值；

23、根据k时刻变量求k+1时刻协方差矩阵p(k+1|k)，其公式为：

24、

25、式中：q表示状态方程计算过程误差的协方差矩阵；

26、步骤s5：使用无迹变换得到新的高斯分布采样点x(i)’(k+1|k)，其公式为：

27、

28、步骤s6：计算得到预测的观测量z(i)(k+1|k)，其公式为：

29、z(i)(k+1|k)＝h[x(i)’(k+1|k)]

30、式中：h[x(i)’(k+1|k)]表示将x(i)’(k+1|k)中的齿条力矩这一变量带入到观测方程中进行计算。

31、步骤s7：根据预测的观测量得到其均值其公式为：

32、

33、计算观测量协方差矩阵其公式为：

34、

35、式中：r表示观测变量的误差协方差矩阵；

36、计算观测量与状态变量的协方差矩降其公式为：

37、

38、步骤s8：计算卡尔曼增益k(k+1)，其公式为：

39、

40、步骤s9：更新k+1时刻无迹卡尔曼滤波的输出状态变量其中包含需要的无迹卡尔曼滤波计算的齿条力矩tr″，其公式为：

41、

42、式中：z(k+1)表示k+1时刻通过传感器获得的观测变量。

43、更新k+1时刻无迹卡尔曼滤波器协方差矩阵p(k+1|k+1)，其公式为：

44、

45、进一步的，观测方程公式为：

46、

47、式中，ea、eb、ec分别为无刷直流电机a、b、c相反电动势，为上一时刻电机转子转角，t为每个时刻间的跨越时间，tr为无迹卡尔曼滤波的观测齿条力矩。

48、进一步的，无迹卡尔曼滤波器系统状态方程的二自由度模型为：

49、

50、

51、式中，cαr为后轮侧偏刚度；cαf为前轮侧偏刚度；lr为汽车后轴到汽车质心点的距离；lf为前轴到汽车质心点的距离；m为汽车质量；iz为绕纵向轴转动惯量；δf为前轮转角；vx为纵向车速；ay为侧向加速度；

52、无迹卡尔曼滤波器系统状态方程的dugoff轮胎模型为：

53、fy’＝-cαf tan αff(λ)

54、

55、

56、式中，fy’为轮胎模型估算的轮胎侧向力；fz为轮胎垂向载荷；λ为切换系数；μ为路面摩擦系数；f(λ)表示切换函数；αf为轮胎侧偏角，其计算公式为：

57、

58、式中：β表示质心侧偏角。

59、进一步的，所述步骤s3中无迹卡尔曼滤波器状态变量预测值的计算公式为：

60、

61、式中：为侧向车速预测值；为横摆角速度预测值；为表示轮胎侧向力预测值；为齿条力矩预测值；τm为机械拖距；τp为气胎拖距；ir为转向柱到车轮的传动比；；c表示轮胎松弛长度。

62、进一步的，摩擦力矩tf的公式为：

63、

64、式中：x表示转向盘转速正负值发生变化的时刻开始计时的时间。

65、进一步的，惯性力矩ta的公式为：

66、

67、式中：ia为转向盘转向柱部分的等效转动惯量；为转向盘转角加速度。

68、进一步的，阻尼力矩td的公式为：

69、

70、式中：为转向盘转角速度；bd表示阻尼系数。

71、进一步的，eps助力矩te的公式为：

72、

73、式中：ts为转向柱转矩。

74、进一步的，最终得到路感反馈转矩tfb的计算公式为：

75、tfb＝tr”+tf+ta+td+te。

76、相较于现有技术，本发明具有以下有益效果：本发明所公开的线控转向系统路感反馈力矩估算方法采用无迹卡尔曼滤波器，能够更适用于汽车这种非线性模型，并且综合了汽车动力学计算路感力矩以及电流传感器检测转向电机电流计算路感力矩的方法，能够估算出更精确的路感反馈力矩，从而为驾驶员提供可靠的路感信息。